Maschinelles Lernen oder auch künstliche Intelligenz (aus dem Englischen: Machine Learning / Artificial Intelligence) basiert auf Algorithmen, die aus Beispielen und Erfahrungen zu lernen, ohne explizit programmiert zu werden. Anstatt Code zu schreiben, speisen Sie Daten in den Algorithmus ein, woraufhin dieser Zusammenhänge in den Daten „erlernt“ (daher der Begriff „maschinelles Lernen“). In den letzten Jahren erfreuen sich verschiedenste Algorithmen des maschinellen Lernens sowie künstliche Intelligenz zunehmender Beliebtheit. Es wird deshalb auch in der angewandten Statistik zunehmend wichtiger, Grundlagen von Techniken wie z.B. Support Vector Machine zu beherrschen. In diesem Blogpost werden wir deshalb die allgemeine Grundlagen des Maschinellen Lernens besprechen. Dabei werden wir auf zwei konkrete Beispiele in R näher eingehen. Hierzu wird Grundlagenwissen in R vorausgesetzt.
Für eine konkrete statistische Beratung im Bereich Machine Learning/Künstliche Intelligenz anhand Ihrer eigenen Daten vereinbaren Sie einfach einen Termin zur Statistik-Beratung bei uns!
Überwachtes vs. Unüberwachtes maschinelles Lernen
Maschinelles Lernen/künstliche Intelligenz ist ein Teilbereich des Data Minings. Dieser Bereich lässt sich dabei grob in zwei Teilbereiche einteilen, dem Überwachten sowie Unüberwachtem Lernen.
Überwachtes maschinelles Lernen: Vorhersage der Ausgabe anhand der Eingabedaten
Beim überwachten Lernen verwendet man Eingabevariablen (X) und Ausgabevariable (y) (zum Beispiel könnte X den Lernaufwand in Stunden für eine Klausur darstellen, während y die resultierende Note ist) und man verwendet einen Algorithmus, um eine Funktion f von der Eingabe zur Ausgabe zu „lernen“.
Y = f (X)
Ziel ist es, die Funktion f so gut anzunähern, dass man mit neuen Eingabedaten (X) die Ausgabevariablen (Y) für diese Daten vorhersagen kann. Verschiedene Algorithmen des überwachten Lernens unterscheiden sich vornehmlich dadurch, wie f gewählt wird.
Wir kennen sozusagen also die richtigen „Antworten“ Y auf die „Fragen“ X. Beispielsweise verfügen wir bereits über Daten von verschiedenen Schülern über Ihren Lernaufwand und der erzielten Noten. Diese Daten könnten wir als Trainingsdaten verwenden. Der Algorithmus macht dann iterativ Vorhersagen über die Trainingsdaten und wird vom Lehrer korrigiert. Das Lernen endet, wenn der Algorithmus ein akzeptables Leistungsniveau erreicht. Für unser Beispiel wäre ein akzeptables Leistungsniveau etwa, wenn der Algorithmus die erzielte Note auf Basis des Lernaufwands mit hoher Wahrscheinlichkeit vorhersagen kann.
Überwachte Lernverfahren lassen sich einteilen in Klassifikations- und Regressionsprobleme. Beispiele hierfür sind Support-Vektor-Maschinen, lineare Regression, logistische Regression, naive Bayes, Entscheidungsbäume, k-Nächster-Nachbar-Algorithmus sowie Neuronale Netze. Wenn von „künstliche Intelligenz“ gesprochen wird, ist oft eines dieser Verfahren gemeint.
Unüberwachten maschinelles Lernen: Versteckte Strukturen der Daten entdecken
Beim unüberwachten Lernen hat man dagegen nur Eingabedaten (X) und keine entsprechenden Ausgangsvariablen. Beispielsweise könnten diese Eingabedaten die Wohnorte von Menschen sein – dann wären Städte die zugehörigen Cluster. Es wäre dann etwa denkbar, dass Restaurantketten aufgrund der Ergebnisse einer Clusteranalyse eine Standortplanung durchführen könnten. Weiterhin wäre es auch denkbar, die Clusteranalyse zu nutzen, um Umfragen auszuwerten und die Antworten in entsprechende Cluster einzuteilen.
Ziel des unüberwachten Lernens ist es, die zugrunde liegende Struktur oder Verteilung in den Daten zu modellieren. Somit kann man dann anhand der Struktur mehr über die Daten erfahren.
Dies wird als unüberwachtes Lernen bezeichnet, da es im Gegensatz zum überwachten Lernen keine richtigen Antworten gibt und es keinen Lehrer gibt. Algorithmen sind ihren eigenen Entwürfen überlassen, um die interessante Struktur in den Daten zu entdecken und darzustellen.
Beispiel Überwachtes Lernen: Support Vector Machine
Ein typischer Vertreter überwachter Lernverfahren sind Support Vector Machines. Bei diesem Verfahren werden Daten mit Hilfe von hochdimensionalen Trennflächen separiert. In diesem Abschnitt wird beschrieben, wie man mit Hilfe des kernlab-Pakets Support Vector Maschinen mit R implementieren kann. Wie wir anschliessend sehen werden, können wir mit Hilfe von R diese Trennflächen einfach visualisieren (solange die Daten 2-dimensional sind). Eine einfache theoretische Einführung findet sich beispielsweise hier.
1. Daten generieren und darstellen
Zunächst werden wir Daten generieren, die nicht linear trennbar sind (es gibt also keine Gerade in 2D, welche die Daten eindeutig in zwei Klassen teilt). Wir erstellen dabei einen zweidimensionalen Vektor von 120 Zeilen (x Є R120 × 2). Die Werte in der ersten Spalte (x1) stammen von einer Normalverteilung mit dem Mittelwert 1 und die Werte in der zweiten Spalte (x2) von einer Normalverteilung mit dem Mittelwert 3.
library(kernlab) # importiere kernlab
library(ggplot2) # importiere ggplot2
set.seed(6) # set.seed sorgt für Reproduzierbarkeit
x = rbind(matrix(rnorm(120), , 2), matrix(rnorm(120, mean = 3), , 2)) # x ist ein 120x2 Vektor normalverteilter Werte mit Mittelwert 1 bzw. 3
y
Zur Visualisierung der Daten verwenden wir anschliessend das Paket ggplot2.Dies ist das geläufigste Paket für eine schnelle und flexible Datenvisualisierungen mit R.
d=data.frame(x=x, y=y) # erstelle
names(d)<-c("x1", "x2", "y")
qplot(x1, x2, data = d, color = factor(y)) + geom_point(shape = 1)
+scale_colour_manual(values = c("#0000FF", "#00FF00"), labels = c("1", "-1"))
Der obige Code zeichnet die Daten auf einem 2-D-Gitter und färbt sie entsprechend ihrer Klasse y ein.
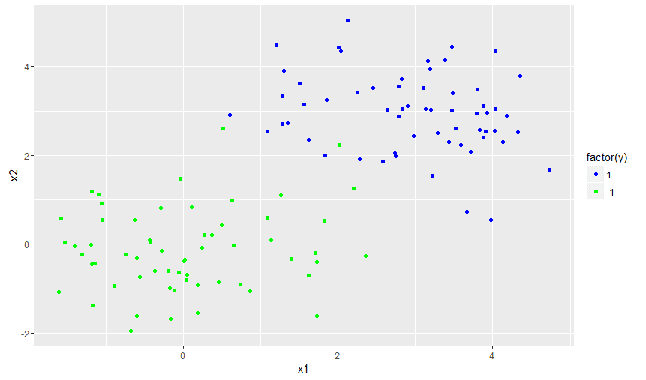
2. Daten Klassifizieren mit linearer Trennfunktion
Wie man leicht erkennen kann, gibt es keine Möglichkeit, die Datenpunkte linear zu trennen, ohne Fehler zu machen. Wenn man dies dennoch tut, führt der Algorithmus eine sogenannte „soft margin“ Klassifizierung durch, wodurch falsch kategorisierte Datenpunkte in Abhängigkeit von ihrer Entfernung von der trennenden Hyperebene bestraft werden. Somit findet der Algorithmus dennoch die beste Trennfläche.
svp = ksvm(y ~ x1 + x2, data = d, type = "C-svc", C = 1, kernel = "vanilladot")
Der folgende Code führt die Support Vector Machine durch.
svp = ksvm(y ~ x1 + x2, data = d, type = "C-svc", C = 1)
Der Parameter C steuert die erwähnte Strafe. Wir werden sehen, dass es für die Generalisierbarkeit der SVM entscheidend ist, einen guten Wert für C zu finden. In diesem Beispielcode ist C auf 1 gesetzt.
Hier können wir nun sehen, wie die Klassifizierungen aussehen:
plot(svp, data = d)
Das Diagramm der resultierenden SVM ergibt einen sogenannten Konturplot, wobei die entsprechenden Unterstützungsvektoren hervorgehoben sind (fett). Es zeigt die gleiche SVM, diesmal jedoch mit C = 100. Offensichtlich versucht die SVM nicht zu missklassifizieren und abzusuchen, da C die Strafe sehr hoch ansetzt:
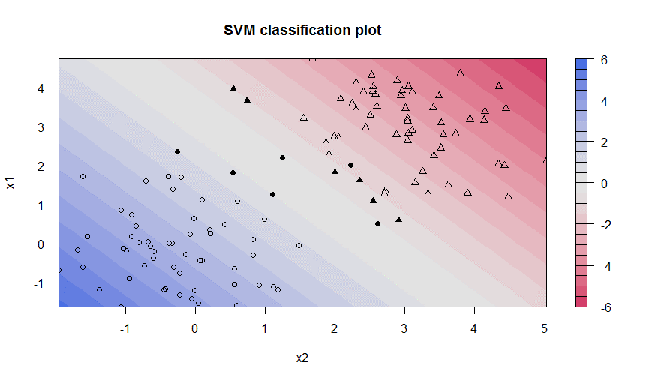
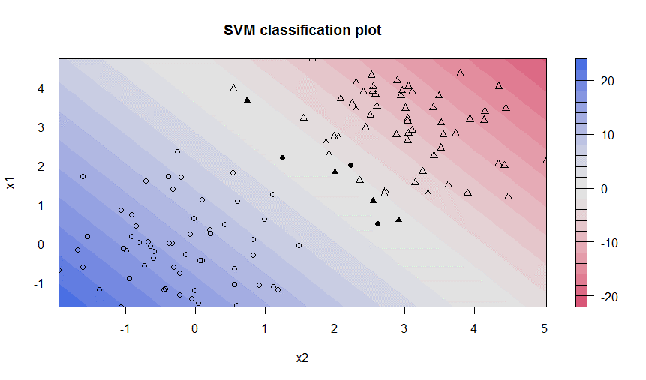
3. Daten klassifizieren mit RBF Trennfunktion
Ein weiterer wichtiger Parameter ist kernel. Dieser Parameter gibt an, wie die Trennfläche konstruiert wird. Versuchen wir, den sogenannten RBF-Kernel anzuwenden:
svp = ksvm(y ~ x1 + x2, data = d, type = "C-svc", C = 1, kernel = "rbfdot")
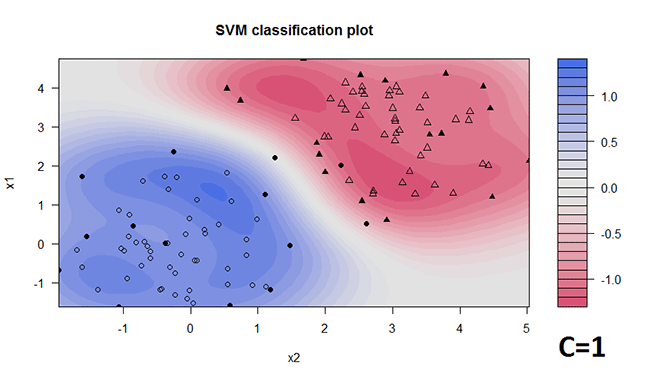
Wir sehen also, dass sowohl die Wahl von C als auch die Wahl der Trennfläche einen großen Einfluss auf das Ergebnis des Algorithmus haben.
Beispiel Unüberwachtes Lernen: k-means Clustering
K-Means-Clustering ist einer der einfachsten und beliebtesten unüberwachten Algorithmen für maschinelles Lernen (ein einfaches theoretisches Beispiel findet sich z.B. hier). Im Folgenden wird ein einfaches angewandtes Beispiel durchgespielt.
Schritt 1: Generierung von geclusterten Daten
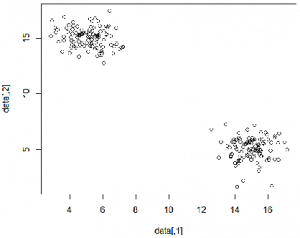
Wir erzeugen wieder 200 zweidimensionale Datenpunkte. Diese verteilen sich dabei um die Werte (15, 5) und (5, 15) herum (mit normalverteilten Abweichungen).
c1 = cbind(rnorm(100, mean=5), rnorm(100, mean=15)) # links oben
c2 = cbind(rnorm(100, mean=15), rnorm(100, mean=5)) # rechts unten
data = rbind(c1, c2) # Binde beide Spalten aneinander (siehe unten)
plot(data)
| c1 | data[,1] | data[,2] |
| 6.370958 | 16.20097 | |
| 4.435302 | 16.04475 | |
| … | … | |
| c2 | 12.99907 | 4.995379 |
| 15.33378 | 5.760242 | |
| … | … |
Schritt 2: Implementation des k-Means-Algorithmus
Für die Implementierung des k-Means-Clustering-Algorithmus existiert in R eine integrierte Funktion namens kmeans. Man muss dabei nur die zu gruppierenden Daten und die Anzahl der Cluster angeben, die wir auf 4 setzen.
cluster = kmeans(data, 4)
cluster
Das Clustering wird anschliessend von R durchgeführt. Wenn wir cluster aufrufen, erhalten wir den folgenden Output:
K-means clustering with 2 clusters of sizes 100, 100
Cluster means:
5.19192 14.997198
14.70764 4.930212
Clustering vector:
1 1 […] 2 2
Within cluster sum of squares by cluster:
258.1744 160.2776
(between_SS / total_SS = 95.8 %)
Available components:
“cluster” “centers” “totss” “withinss” “tot.withinss” “betweenss” “size” “iter” “ifault”
Der obige Output sagt Folgendes aus:
- was getan wurde (Clustering mit 2 Clustern der Größen 100, 100)
- die Zentroide der Cluster, also ihre zentralen Punkte (das ist ziemlich nahe an dem, was wir erwarten würden – die Daten stammen von bivariaten Normalverteilungen mit Mitteln (5, 15) und (15, 5)) (cluster means)
- ein Vektor mit 200 Einträgen, der die zugewiesenen Kennzeichnungen jedes Datenpunkts beschreibt (clustering vector)
- und die Summe der Quadrate pro Cluster innerhalb des Clusters – dies ist die Summe der quadratischen Abweichungen für jeden Datenpunkt vom jeweiligen Cluster-Schwerpunkt (Within cluster sum of squares by cluster)
Schritt 3: Visualisierung der Ergebnisse
# Zeichne Daten verschiedener Farbe
plot(data, col = kk$cluster)
# Plotte die Mittelpunkte in Schwarz
points(kk$centers, pch = 16, cex = 2)
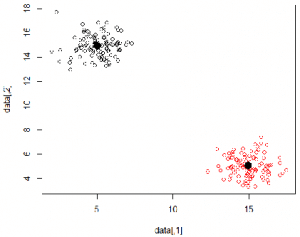
Das war ein sehr einfaches Beispiel mit zwei schön getrennten Punktclustern. In praktischen Anwendungen für künstliche Intelligenz sind die Punkte jedoch oftmals höherdimensional und damit nicht mehr einfach zu visualisieren. Falls Sie Hilfe bei Ihrem statistischen Projekt benötigen, kontaktieren Sie uns gerne!
Zusammenfassung
In diesem Artikel haben wir eine erste Einführung in die Grundlagen des maschinellen Lernens gegeben. Dabei haben wir den Unterschied zwischen überwachten und unüberwachten Lernen dargestellt:
- Überwachtes Lernen: Alle Daten werden gelabelled und die Algorithmen lernen, die Ausgabe aus den Eingangsdaten vorherzusagen.
- Unüberwachtes Lernen: Alle Daten sind nicht gelabelled und die Algorithmen lernen aus den Eingabedaten die inhärente Struktur.
In den letzten Jahren haben viele Techniken des Maschinellen Lernens / Künstliche Intelligenz in der Statistik an Bedeutung gewonnen. Beispiele hierfür sind Support-Vektor-Maschinen, lineare Regression, logistische Regression, naive Bayes, Entscheidungsbäume, k-Nächster-Nachbar-Algorithmus, Neuronale Netze sowie k-means Clustering. Falls Sie Hilfe bei der Auswahl und Durchführung ihres Data Mining-Projekts brauchen, helfen unsere Experten gerne mit Ihrem persönlichen Statistik-Projekt!