Cohen’s d soll helfen, die Stärke eines gemessenen Unterschieds im arithmetischen Mittel zwischen zwei Gruppen zu bestimmen. Denn nicht jeder beobachtete Effekt, der statistisch signifikant ist, ist auch in der Praxis bedeutsam. Bei grossen Datenmengen können auch kleine Differenzen signifikant und aussagekräftig sein.
Wie die Korrelationskoeffizienten gehört Cohen’s d daher zu den Kennzahlen zur Messung der Effektstärke. Benannt ist die Kennzahl nach dem Statistiker und Psychologen Jacob Cohen.
Sie möchten Unterstützung bei der Berechnung und Anwendung von Cohen’s d? Wenden sie sich hierzu an uns für eine professionelle Statistik Beratung.
Cohen’s d Effektstärke: ein Beispiel
Zum Einstieg starten wir gleich mit einem Beispiel: Eine Gruppe von Studierenden erhielt vor einer Prüfung eine zusätzliche Unterrichtsstunde. Die erreichte Punktezahl lag in dieser Gruppe mit durchschnittlich 173 tatsächlich über jener der Gruppe, die keinen zusätzlichen Unterricht erhielt und nur 167 Punkte erreichte.
Ein Signifikanztest bewertet das Ergebnis als signifikant. Doch wie relevant ist diese Differenz in Relation zu den Unterschieden, die es innerhalb der beiden Gruppen gibt?
Diese Frage lässt sich mit Cohens d beantworten. Ein grosser Vorteil der Kennzahl ist die Einfachheit der Formel, sie lautet:
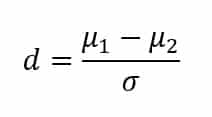
Konkret wird also die Differenz zwischen den beiden arithmetischen Mittelwerten (µ1, µ2) durch die Standardabweichung (σ) geteilt. Dabei wird zunächst unterstellt, dass die Standardabweichung für beide Teilgruppen gleich ist.
Üblicherweise ist das allerdings nicht der Fall. Dann verwenden wir die sogenannte gepoolte Standardabweichung.
Gepoolte Standardabweichung bei gleich grossen Gruppen
Die Berechnung ist einfach, wenn beide Untersuchungsgruppen gleich gross sind. Haben 50 Studierende eine Zusatzstunde erhalten und 50 nicht, dann ist die gepoolte Standardabweichung die Wurzel aus dem Durchschnitt der beiden Varianzen.
Stellen wir uns vor, die Standardabweichung beträgt für die Gruppe mit Zusatzunterricht 34,64 Punkte, für jene ohne 44,72. Die Varianzen betragen also 1.200 und 2.000, da die Varianz sich als Quadrat der Standardabweichung berechnet.
Aus 1.200 und 2.000 nehmen wir das arithmetische Mittel, also 1600. Dieser Wert ist unsere gepoolte Varianz, die Wurzel daraus ergibt die gepoolte Standardabweichung von 40.
Gepoolte Standardabweichung bei unterschiedlich grossen Gruppen
Sind beide Gruppen unterschiedlich gross, also mit unterschiedlicher Stichprobengrösse n, dann müssen die Standardabweichungen (s1, s2) gewichtet werden.
Die Gewichtung erfolgt allerdings nicht mit der Gruppengrösse n, sondern mit der Gruppengrösse n-1. Entsprechend der beiden Stichproben wird durch die Fallzahl n1+n2-2 geteilt:
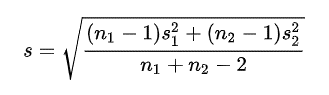
Im Konkreten Beispiel: Haben 20 Personen am Zusatzunterricht teilgenommen, 80 aber nicht, wird die Varianz für die Teilnehmenden mit 20-1 = 19 multipliziert, die für die Kontrollgruppe mit 80-1 = 79.
Beide Ergebnisse werden anschliessend zunächst addiert und dann durch: 20+80-2 = 98 geteilt.
Das Ergebnis ist die gepoolte Varianz, auch in diesem Fall müssen wir die Quadratwurzel daraus ziehen, um die gepoolte Standardabweichung zu erhalten.
Cohen’s d Interpretation der Effektstärke
Wie sieht nun die Cohens d Interpretation im obigen Beispiel mit den gleich grossen Gruppen aus?
Die gepoolte Standardabweichung haben wir ermittelt mit einem Wert von 40. Cohen’s d berechnet sich nun aus der Differenz zwischen den beiden Mittelwerten geteilt durch 40, im Beispiel: (173-167)/40 = 6 / 40 = 0,15.
Anschaulich gesprochen setzt Cohen’s d den Unterschied zwischen zwei Mittelwerten in Relation zur durchschnittlichen Streuung. Vereinfacht gesagt ist bei Werten > 1 die Streuung innerhalb der Gruppen grösser als der Unterschied zwischen den Gruppen.
Aussagekräftiger bei der Interpretation von Cohen’s d ist aber eine Einteilung, die Jacob Cohen selbst aufgestellt hat. Demnach sind alle Werte unter 0,2 sehr gering bis vernachlässigbar, Werte von 0,2 bis unter 0,5 stehen für einen geringen Effekt, solche von 0,5 bis unter 0,8 für einen mittleren und Werte ab 0,8 für einen starken Effekt.
| Untergrenze | Obergrenze | Effektstärke |
| Von 0 | bis unter 0,2 | kein bzw. sehr geringer Effekt |
| Von 0,2 | bis unter 0,5 | geringer Effekt |
| Von 0,5 | bis unter 0,8 | mittlerer Effekt |
| Ab 0,8 | und darüber | starker Effekt |
Der von uns gemessene Effekt wäre nach dieser Tabelle demnach sehr gering. Dieser Wert allein gibt allerdings noch keine ausschliessliche Auskunft darüber, ob eine Massnahme sinnvoll ist oder nicht. Das ist auch von anderen Faktoren (wie zB. Kosten, etc.) abhängig.
Folglich erlaubt der statistisch berechnete Wert allein in letzter Konsequenz keine eindeutige Beantwortung der Fragestellung. Allerdings kann die Statistik die Entscheidungsgremien mit der Information versorgen, dass der Effekt des Zusatzunterrichts in diesem Fall gering wäre.
Wofür brauche ich die Standardabweichung in der Formel?
Auf den ersten Blick scheint bereits die (geringe) Differenz zwischen den beiden Mittelwerten die gewünschte Information zu bieten. Doch so einfach ist es nicht:
Bei einer geringen Streuung, also einer niedrigen Standardabweichung, kann auch ein scheinbar kleiner Unterschied zwischen den Mittelwerten schon einen bedeutenden Effekt bewirken. Aus eben diesem Grund wird in vielen Signifikanztests die Standardabweichung verwendet.
Cohen’s d berechnen: Excel
Excel kennt keine Formel für die Berechnung von Cohens da, allerdings ist die Berechnung mit wenigen Schritten möglich.
Zunächst werden die arithmetischen Mittel mit der Formel =mittelwert() berechnet und mittels einfacher Subtraktion die Differenz bestimmt.
Anschliessend errechnen wir die jeweiligen Varianzen mit der Formel =varianz(). Diese Formel berechnet die reguläre Varianz (also nicht die Stichprobenvarianz) und ignoriert logische Werte und Texte.
Sind beide Gruppen gleich gross, wird aus beiden Varianzen mit der Formel =mittelwert() das arithmetische Mittel berechnet. Sind die Gruppen unterschiedlich gross, wird die Varianz jeweils mit der Zahl der Fälle in der entsprechenden Gruppe multipliziert und anschliessend – wie oben beschrieben – durch die Fallzahl – 2 dividiert.
Aus dieser gepoolten Varianz wird mit der Formel =wurzel() die Quadaratwurzel berechnet, damit erhalten wir die gepoolte Standardabweichung. Abschliessend wird die Differenz der beiden Mittelwerte durch diese gepoolte Standardabweichung geteilt, und das Ergebnis ist unser Cohen’s d.
Cohen’s d berechnen: SPSS
Statistikprogramme erleichtern für gewöhnlich die Berechnung. Allerdings kennt auch SPSS keinen Befehl, um Cohen’s d direkt zu berechnen.
Wie in Excel müssen zunächst die Mittelwerte und dann die beiden Varianzen separat berechnet werden. Aus den Varianzen wird dann die gepoolte Standardabweichung errechnet. Das geht am einfachsten mit einer Hilfsrechnung in Excel (siehe oben).
Cohen’s d berechnen: R
In der Statistiksoftware R lässt sich Cohen’s d dagegen sehr einfach berechnen. Mehrere Pakete enthalten Formeln zur Berechnung von Cohen’s d (zB. Psych und lsr). Zu beachten gilt, dass die Befehle und die Struktur nicht gleich sind: In Psych lautet die Formel cohen.d, in lsr cohensD. Wie in R üblich, ist auf Gross- und Kleinschreibung zu achten.
Besonders einfach ist die Formel in lsr: Hier werden einfach die Namen der beiden Variablen, verbunden mit einem ‘-‘ , eingegeben. Im nachstehenden Beispiel heisst unser Datenset einfach Data, unsere Variable mit den Prüfungsergebnissen heisst Ergebnis, und die Variable Unterricht gibt Auskunft darüber, ob die Studierenden Zusatzunterricht bekommen haben oder nicht.
Die Formel für die Berechnung lautet daher: cohensD(Data$Ergebnis-Data$Unterricht).
Fazit
Cohen’s d ist eine einfache und aussagekräftige Möglichkeit, die Effektstärke zu bestimmen, wenn die Mittelwerte zweier Gruppen verglichen werden. Eine Gruppe kann beispielsweise eine bestimmte Behandlung bekommen haben, eine andere nicht.
Aber auch andere Gruppenmittelwerte, etwa Frauen und Männern, lassen sich vergleichen. Die Formel ist auch aufgrund der einfachen Berechnung attraktiv, etwas aufwändiger gestaltet sich lediglich die Berechnung der gepoolten Standardabweichung bzw. die Berechnung in SPSS.
Bei weiteren Fragen freuen wir uns über Ihre schriftliche Kontaktaufnahme über unser Anfrageformular. Gerne unterstützen wir Sie und erstellen Ihnen umgehend unverbindlich ein individuelles Angebot!
Weiterführende Links
- Psychometrica: Effektstärke
- Cohen’s d