Ist mein Ergebnis signifikant? Ist mein p-Wert kleiner als das Signifikanzniveau? Diese oder ähnliche Fragen kreisen um viele statistische Untersuchungen. Oft wird die Signifikanz dabei gleichgesetzt mit bedeutend, herausragend und wichtig. Nicht signifikante Ergebnisse werden als irrelevante Studien abgetan.
Dabei ist die Signifikanz lediglich eine Entscheidungsregel, eine ja/nein Aussage, die nichts über den Informationsgewinn einer Studie aussagt. Wie statistische Ergebnisse richtig zu interpretieren sind, lesen sie in diesem Beitrag.
Folgende Fragen werden in diesem Artikel beantwortet
- Warum sind Fehlentscheidungen bei statistischen Tests unvermeidbar?
- Was versteht man unter Fehler 1. Art und Fehler 2. Art?
- Was hat es mit dem Signifikanzniveau auf sich und was sind signifikante Ergebnisse?
- Welche Fehler darf man in der Interpretation des Testergebnisses nicht machen?
Hypothesen auf der Anklagebank: die Idee des statistischen Tests
Für das Verständnis der Idee des statistischen Tests hilft es, sich das Bild einer Gerichtsverhandlung vor Augen zu führen.

Vor Gericht muss der Richter oft eine Entscheidung zwischen der Position des Klägers und des Angeklagten finden. Da der Richter bei der Tat nicht dabei war, muss er anhand der Zeugenaussagen und Beweisen entscheiden. Ein statistischer Test funktioniert ganz ähnlich: Es dreht sich alles um eine Entscheidung, ob sich die Beweislage zufällig zugetragen haben könnte. Die wahren Umstände sind unbekannt. Ein Test muss eine Entscheidung basierend auf einer Stichprobe und dem Signifikanzniveau treffen.
Dazu stellt man zunächst Hypothesen auf. In der Alternativhypothese wird formuliert, was zu belegen ist. In der Nullhypothese wird dagegen der „Standard“ Zustand beschrieben, die Situation, die all das umfasst, was man nicht nachweisen will. Ein Beispiel für eine Alternativhypothese wäre also: „Der Wirkstoff lindert die Symptome“ die entsprechende Nullhypothese wäre: „Der Wirkstoff lindert die Symptome nicht“. Im nächsten Schritt muss man ähnlich einem Richter im Gerichtssaal eine Entscheidung finden, welche der beiden Aussagen bzw. Hypothesen weiterhin anzunehmen ist. Und wie vor Gericht gilt auch hier der Grundsatz: „Im Zweifel für den Angeklagten“. Der „Angeklagte“ ist hier die Nullhypothese. Der Statistiker nimmt die Rolle eines Richters ein und entscheidet anhand der Datenlage ob weiterhin von der in der Nullhypothese formulierten Aussage auszugehen ist. Oder sprechen die Daten eindeutig genug dafür, um in Zukunft von der Alternativhypothese H1 auszugehen?
Im Zweifel für den Angeklagten: Fehler 1. Art und Fehler 2. Art
Die gesammelten Daten dienen dabei als „Beweismittel“ zur Entscheidungsfindung. Die Wahrheit dahinter kennt weder der Richter noch der Statistiker. Und so ist es möglich, dass auch Fehlentscheidungen getroffen werden:
| Testergebnis: Nullhypothese annehmen | Testergebnis: Nullhypothese ablehnen | |
| Nullhypothese wahr |
Korrekt |
Fehler 1. Art α-Fehler |
| Nullhypothese falsch |
Fehler 2. Art β-Fehler |
Korrekt |
Von einem Fehler 1. Art oder α-Fehler spricht man dann, wenn im statistischen Test H0 verworfen wird. Die Alternativhypothese wird angenommen, obwohl diese in Wahrheit gar nicht gilt. Beispielsweise, man entscheidet aufgrund der Datenlage, dass ein neuer Wirkstoff die Symptome lindert, obwohl er tatsächlich wirkungslos ist.
Der Fehler 2. Art oder β-Fehler entsteht dadurch, dass das Testergebnis H0 bestätigt wird, obwohl in Wahrheit die Alternativhypothese gilt. Im obigen Beispiel bedeutet dies folgende Testentscheidung: Der Wirkstoff lindert nicht die Symptome, obwohl er tatsächlich wirksam ist.
Die Möglichkeit eines Fehlers ist unvermeidbar und jeder Anwender nimmt dieses Risiko bei Anwendung eines statistischen Tests in Kauf!
Die beiden Fehlertypen Fehler 1. Art und Fehler 2. Art stehen in Zusammenhang. Dies sieht man besonders deutlich, wenn man sich extreme Entscheidungsregeln oder Tests betrachtet: Wenn ein Test bei jeder Datenlage H0 annimmt, kann ein Fehler 1. Art nicht eintreten. Das heisst, die Alternative kann nie angenommen werden, unabhängig davon, was die Daten sagen. Sollte die Alternativhypothese jedoch in Wirklichkeit stimmen, beträgt die Wahrscheinlichkeit für einen Fehler 2. Art 1 (100%).
Der andere Extremfall ist eine Entscheidungsregel, die sich immer für die Alternative entscheidet. Sollte H0 jedoch stimmen, würde man in jeden Fall einen Fehler 1. Art von 100% erhalten.
Beide Extremtests sind aber in der Praxis unbrauchbar: Diese liefern deterministische Ergebnisse fernab der dargebrachten Beweise, den Daten.
Dazu kommt, dass die Entscheidungen in ihren Konsequenzen nicht gleichbedeutend sind:
Lehnt man die Nullhypothese ab, obwohl sie in Wahrheit gilt, sind die Auswirkungen wesentlich bedeutender: Ein Fehler 1. Art vor Gericht ist gleichbedeutend mit der Verurteilung eines Unschuldigen, ein Fehler 2. Art mit der Freilassung eines Verbrechers. Im Zweifel für den Angeklagten lautet ein Grundsatz unseres Rechtswesens. Und diese Grundidee gilt auch für das statistische Testen: Im Zweifel für H0! Der Fehler 1. Art wird durch das Signifikanzniveau unter Kontrolle gehalten! Wenn ein neuer Wirkstoff nicht eindeutig nachweisen kann, dass er deutlich genug die Symptome lindert, kann er sich nicht durchsetzen gegenüber der Standardtherapie.
Erdrückende Beweislast: das Signifikanzniveau α

Wann sind die Beweise erdrückend genug? Im Gerichtsaal muss die Antwort auf diese Frage der Richter finden, in der Statistik gibt es dafür Kriterien: Die Schranke, ab wann man von eindeutigem Nachweis sprechen kann, erfolgt in der statistischen Testung mithilfe des Signifikanzniveaus.
Vor Durchführung des Tests wird ein Signifikanzniveau festgelegt, meist bei 5%. Das Signifikanzniveau gibt die maximal erlaubte Wahrscheinlichkeit für einen Fehler 1. Art an. Es ist damit eine vorher vereinbarte Schmerzgrenze.
P-Werte unterhalb des Signifikanzniveaus werden als „Beweis“ für die Alternative angesehen. Je kleiner der p-Wert, umso unwahrscheinlicher ist die Nullhypothese. Umgangssprachlich wird das Ergebnis dann als signifikant bezeichnet.
P-Werte geben die Wahrscheinlichkeit an, dass die erhobenen Daten oder in Richtung Alternativhypothese noch extreme Daten vorkommen, unter der Voraussetzung, dass die Nullhypothese gilt.
Die Festlegung des Signifikanzniveaus ist prinzipiell beliebig. Die traditionellen Grenzen von 5% bzw. 1% stammen aus einer Zeit, in der Tests noch manuell mit Stift und Unmengen von Verteilungstabellen berechnet wurden. Die zugehörigen Werte waren gut abzulesen. Heutzutage kann man die p-Werte meist exakt berechnen. Die 5% Festlegung für das Signifikanzniveau ist aber bis heute weit verbreitet.
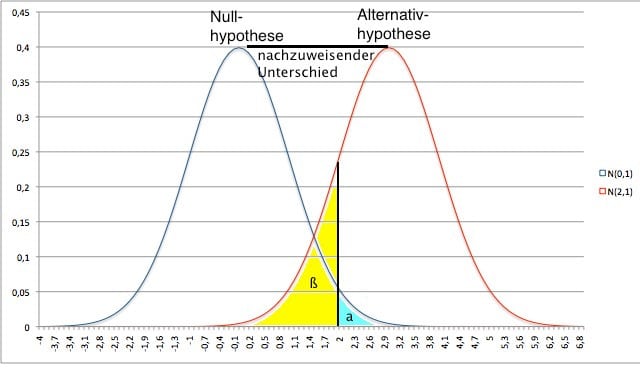
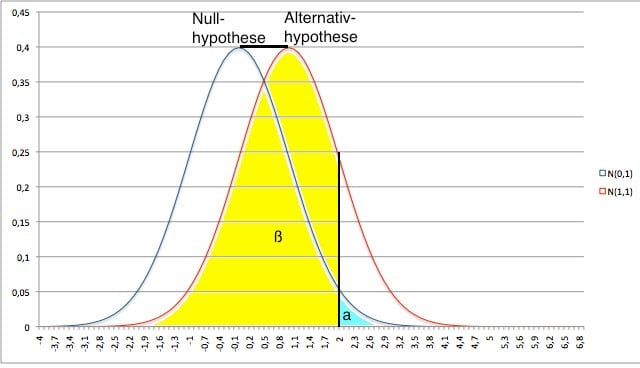
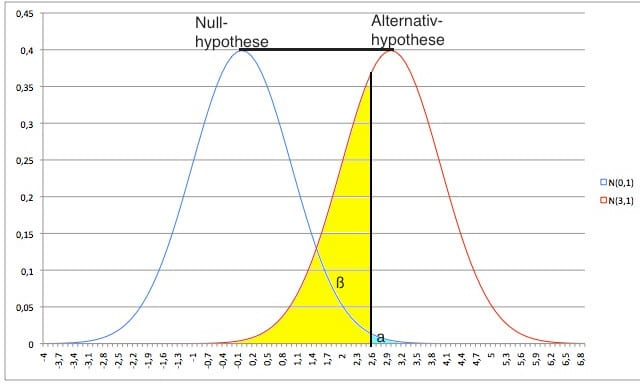
Der Fehler 2. Art ist indirekt proportional zum Fehler 1. Art: Je höher der eine, desto niedriger der andere Fehler. Neben dem α-Fehler spielen noch weitere Faktoren eine wichtige Rolle für die Höhe des β-Fehlers. Die Zusammenhänge sind in folgender Tabelle zusammengestellt:
| Gerichtsszene | Anzahl der Beweise | Fehler, einen Unschuldigen zu verurteilen | Deutlichkeit der Gesetzesübertretung | Unterschiedlichkeit der Beweise |
| Statistik | Stichprobenumfang | Fehler 1. Art | nachzuweisender Unterschied | Streuung der Daten |
| Fehler 2. Art |




Der Fehler 2. Art kann nicht im Studienverlauf berechnet werden, er wird bei der Studienplanung im Rahmen der Fallzahlplanung berücksichtigt. Wenn Sie Unterstützung zum Thema Fallzahlplanung benötigen, können wir Sie gerne mit einer Statistik Beratung unterstützen.
Im Folgenden ist eine Illustration des Zusammenhangs von α, β und dem nachzuweisenden Effekt am Beispiel einer normalverteilten Testgrösse zu sehen.
Signifikanz, Signifikanzniveau und Co.: Fehler in der Interpretation
Statistische Tests sind immer wieder in der Diskussion. Ein Grund dafür ist häufig die falsche Interpretation eines statistischen Tests.
Eine Falschannahme besteht sicherlich darin, signifikant als bedeutend oder wichtig zu interpretieren. Damit wären nur Studien wichtig, die signifikante Ergebnisse liefern. Das ist aber absolut unrichtig. Der Test liefert lediglich eine Entscheidungshilfe oder ein Kriterium, er sagt nichts über die Wichtigkeit der Fragestellung aus.
Studien mit sehr hoher Fallzahl führen auch bei geringen Effekten zu sehr geringen p-Werten. Kleine und in der Praxis evtl. unbedeutende Unterschiede sind signifikant. Was würden Sie zu einem Justizsystem sagen, bei dem geringfügige Gesetzesübertretungen schon geahndet werden und zu Verurteilungen führen?
Ein signifikanter p-Wert wird häufig so interpretiert, dass die Wahrscheinlichkeit eines Fehlalarms unter 5% liegt. Dies ist falsch. Das kann ein Test nicht aussagen, da der p-Wert unter der Bedingung gebildet wird, dass die Nullhypothese gilt. Ein Umkehrschluss von der Stichprobe auf die zugrunde liegende Gesamtheit, die Realität ist nicht möglich. Es fehlt die Information über die Wahrscheinlichkeit, dass der gesuchte Effekt selbst auftritt.
Eine weitere wichtige Tatsache, die z. T. unbeachtet bleibt, besteht darin, dass bei einem Signifikanzniveau von 5% eine von 20 äquivalent durchgeführten Studien ein signifikantes Ergebnis liefert, obwohl in Wahrheit kein Effekt vorliegt. Meist wird genau die eine signifikante Studie veröffentlicht. Dadurch entsteht ein sogenannter Publikationsbias.
Zusammenfassung
In diesem Artikel haben wir Ihnen einen Einblick in die Konzepte der statistischen Testung gegeben und Fehler 1. Art oder α-Fehler, Fehler 2. Art oder ss-Fehler und die Power eines Tests näher erläutert. Die Fehler sind voneinander abhängig, es wird immer der ss-Fehler durch das Signifikanzniveau α kontrolliert. Den ss-Fehler kann man in der Studienplanung anhand der Fallzahlplanung einbeziehen, in der eigentlichen Testung ist er nicht mehr beeinflussbar. Diese Fehler sind Bestandteile jedes statistischen Tests.
Schwerwiegend sind häufig die Fehler, die bei der Interpretation des Ergebnisses statistischer Tests gemacht werden. Ein statistischer Test kann keine Aussage über die Korrektheit einer Hypothese treffen!
Wenn Sie unsicher bezüglich der Interpretation ihrer Testergebnisse sind, oder wir Ihre Schlussfolgerungen überprüfen sollen, sind wir gerne für Sie da. Bei Fragen oder Problemen rund um statistische Auswertung und Ergebnisdarstellung und allen anderen statistischen Belangen stehen unsere Experten von Novustat Ihnen gerne zur Seite.
Weiterführende Quellen:
[1] Wikipedia Artikel zur statistischen Signifikanz
[2] Artikel über Kontroversen rund um das Signifikanzniveau (Spektrum)
