Für viele statistische Auswertungen spielt die Wahrscheinlichkeitsverteilung eine zentrale Rolle. Egal ob Sie Daten für eine Qualitätskontrolle, eine Analyse der Kundenzufriedenheit oder für die Optimierung von Produktionskapazitäten auswerten: Für alle diese Analysen sind Wahrscheinlichkeitsverteilungen ein zentrales Konzept – daher ist ein Verständnis der jeweils relevanten Wahrscheinlichkeitsverteilung unerlässlich! Wir zeigen Ihnen die fünf wichtigsten Verteilungen und beispielhafte Anwendungen. Für eine detaillierte Beratung zum Thema Wahrscheinlichkeitsverteilung und Datenauswertung steht Ihnen zusätzlich unsere Statistik Hilfe zur Verfügung!
Mit Hilfe einer Wahrscheinlichkeitsverteilung lassen sich zufallsbehaftete Ereignisse oder Variablen (sogenannte Zufallsvariablen) modellieren. Beispielsweise werden etwa Ereignisse wie Münzwürfe, Würfeln oder auch die Körpergrösse von Personen beschrieben. Hierbei weisen Wahrscheinlichkeitsverteilungen einem Ereignis (zum Beispiel dem Würfeln einer {5}) eine Wahrscheinlichkeit zu (im Falle eines fairen Würfels ).
Stetige und diskrete Wahrscheinlichkeitsverteilungen
Man unterscheidet im Allgemeinen stetige (kontinuierliche) und diskrete Wahrscheinlichkeitsverteilungen. Bei stetigen Wahrscheinlichkeitsverteilungen kann das Zufallsereignis jeden Wert in einem Intervall annehmen (z.B. die exakte Körpergrösse eines Menschen) – bei diskreten Wahrscheinlichkeitsverteilungen kann das Zufallsereignis nur bestimmte Werte annehmen (z.B. Würfeln).
Wichtige Begriffe im Zusammenhang von Wahrscheinlichkeitsverteilungen sind die Dichtefunktion sowie die Verteilungsfunktion. Diese beiden Funktionen bestimmen Wahrscheinlichkeitsverteilungen eindeutig, indem sie die aufgetretenen Frequenzen (auf der y-Achse) von bestimmten Zufallsgrössen (auf der x-Achse) bei wiederholter Durchführung beschreiben. Beim fairen Würfel wäre zum Beispiel die Frequenz des Auftretens von einer bestimmten Zahl von 1-6 auf der y-Achse und die jeweilige Augenzahl auf der x-Achse zu finden.
| Stetige Verteilung | Diskrete Verteilung | Fragestellung |
| Dichtefunktion (probability density function) | Wahrscheinlichkeitsfunktion (probability mass function) | Wie wahrscheinlich ist ein spezifisches Szenario am Wert x? z.B. Wie wahrscheinlich ist das Würfeln einer 6? |
| Verteilungsfunktion (cumulative distribution function) | Mit welcher Wahrscheinlichkeit tritt irgendein Ereignis aus der Menge (alle reellen Zahlen kleiner oder gleich x) ein. z.B. Wie wahrscheinlich ist das Würfeln einer Zahl kleiner oder gleich 4? | |
1 – Normalverteilung: die wichtigste Wahrscheinlichkeitsverteilung
Im folgenden Teil wird immer die Dichtefunktion (für stetige Verteilungen) bzw. Wahrscheinlichkeitsfunktion (für diskrete Verteilungen) visualisiert.
Die Normalverteilung oder Gauss-Verteilung ist eine stetige Verteilung (das heisst, es können alle reellen Zahlen angenommen werden) und stellt die wichtigste Wahrscheinlichkeitsverteilung dar.
Die Dichtefunktion ist dabei durch die sogenannte Gausssche Glockenkurve gegeben. Die beiden Parameter (µ und ) geben Mittelwert sowie Standardabweichung der Normalverteilung an.
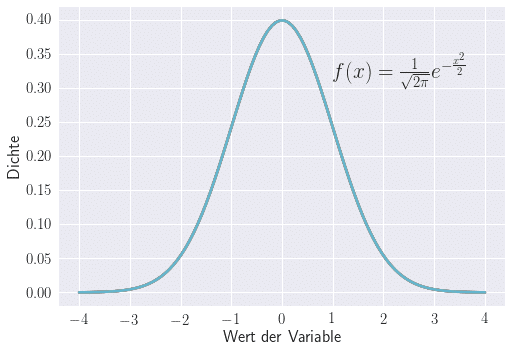
Anwendung
Normalverteilte Zufallsvariablen finden sich in der Praxis sehr häufig wieder. Beispielhafte Anwendungen sind biologische Grössen (etwa Körpergrössen innerhalb eines Geschlechts, Intelligenzquotienten oder Sozialkompetenz), physikalische Sachverhalte (durchschnittliche Sonnenscheindauer an einem bestimmten Tag des Jahres), statistische Fehler (etwa bei Regressionsanalysen oder im Zusammenhang mit statistischen Tests) sowie Qualitätskontrollen (etwa die Dicke eines Brettes in einer Sägerei).
Der Hauptgrund für die Wichtigkeit der Normalverteilung ist jedoch der zentrale Grenzwertsatz. Der zentrale Grenzwertsatz besagt, dass unter bestimmten allgemeinen Voraussetzungen die Summe aus n unabhängigen, identisch verteilten Zufallsvariablen wiederum normalverteilt ist.
Als Beispiel hierfür sei der Wurf von n fairen Würfeln genannt: Wenn man man nur einen Würfel wirft, so ist jede Augenzahl gleich wahrscheinlich. Wirft man hingegen viele Würfel, so wird die mittlere Augenzahl durch die Normalverteilung beschrieben – siehe die folgende Abbildung (eine weitere schöne Visualisierung dieses Beispiels findet sich z.B. hier).
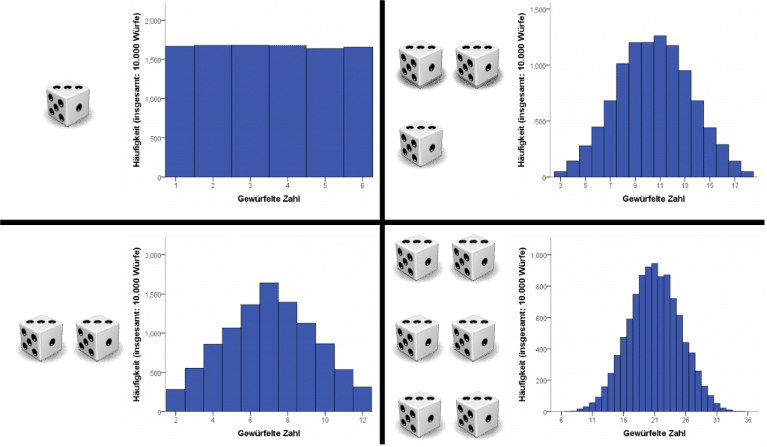
2 – t-Verteilung: Normalverteilung für kleine Stichprobengrössen
Wie oben erwähnt wird die Normalverteilung bei vielen statistischen Verfahren eingesetzt. Allerdings unterschätzt die Normalverteilung bei kleinen Stichprobenumfängen bestimmte statistische Grössen. Dieser Effekt kann aber ausgeglichen werden, indem man bei manchen statischen Verfahren statt der Normalverteilung die t-Verteilung einsetzt.
Die t-Verteilung ist eine der Normalverteilung verwandte Verteilung. Die t-Verteilung erhält man, wenn man den Mittelwert einer normalverteilten Population in Situationen schätzt, in denen der Stichprobenumfang klein ist und die Standardabweichung der Population unbekannt ist. Diese Verteilung zeichnet sich dadurch aus, dass Sie breitere Enden als die Normalverteilung hat.
Für steigende Stichprobenumfänge nähern sich die beiden Verteilungen an und sind schliesslich identisch.
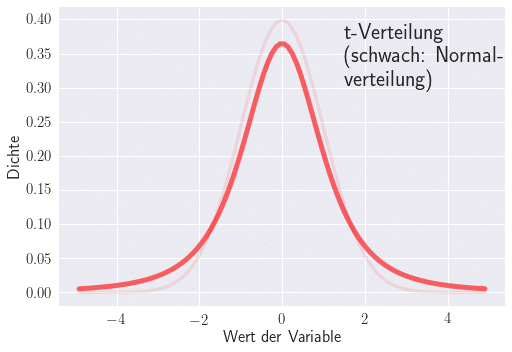
Anwendung
Die t-Verteilung spielt besonders in statistischen Analysen eine wichtige Rolle. Sie wird vor Allem für Hypothesentests und Konfidenzintervalle benötigt. In diesen Situationen interessiert man sich nämlich für die Verteilung des Stichprobenmittelwerts. In der Praxis ist die Varianz für den Stichprobenmittelwert aber fast immer unbekannt und wird durch die Stichprobenvarianz geschätzt.Dann ist der Mittelwert der Stichprobe nicht normalverteilt, sondern t-verteilt mit n−1 Freiheitsgraden. Sollten Sie Unterstützung bei Ihrer statistischen Arbeit benötigen, können wir Sie gerne mit einer Statistikberatung unterstützen.
3 – Poisson-Verteilung: Wann immer Sie Zählgrössen modellieren möchten
Die Poisson-Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung, welche die Verteilung von Zählgrössen beschreibt. Oder mit anderen Worten: Wie oft tritt ein bestimmtes, zählbares Ereignis ein, wenn man es sehr oft wiederholt?
Der Parameter gibt hierbei die mittlere Ereignisrate an.
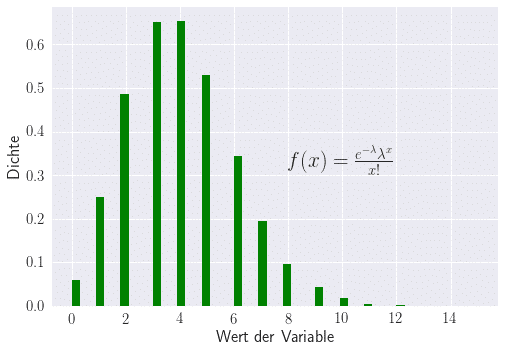
Anwendung
Ein klassisches Beispiel für die Anwendung der Poisson-Verteilung ist die Anzahl der Soldaten der preussischen Armee, die pro Jahr durch einen Pferdetritt versehentlich getötet wurden. Weitere Beispiele sind die Anzahl der Mutationen auf einem bestimmten DNA-Strang pro Zeiteinheit oder die Anzahl der Besucher einer Website pro Minute, Stunde oder Tag.
4 – Exponentialverteilung: Modellierung von Wartezeiten
Die Exponentialverteilung ist eine durch Exponentialverteilungen beschriebene stetige Verteilung (siehe Bild), welche zur Modellierung der Dauer zufälliger Zeitintervalle genutzt wird. Der Parameter steht hierbei für die Zahl der erwarteten Ereignisse pro Zeitintervall.
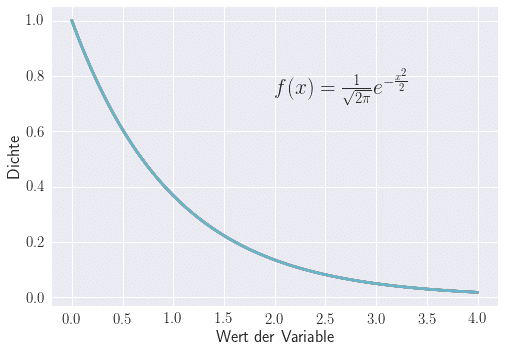
Anwendung
Der typischste Anwendungsfall der Exponentialverteilung ist die Lebensdauer von Menschen, Teilen von Maschinen oder auch die Zeit zwischen zwei Anrufen in einem Callcenter. Auch wird die Lebensdauer von zerfallenden Teilchen in der Physik durch die Exponentialverteilung approximiert.
5 – Gleichverteilung: Wann immer es um gleich wahrscheinliche Ereignisse geht
Die Gleichverteilung ist ein Sonderfall unter den Wahrscheinlichkeitsverteilungen, denn sie existiert sowohl als stetige als auch als diskrete Verteilung. Sie beschreibt hierbei Ereignisse, bei denen jeder Wert gleich wahrscheinlich ist.
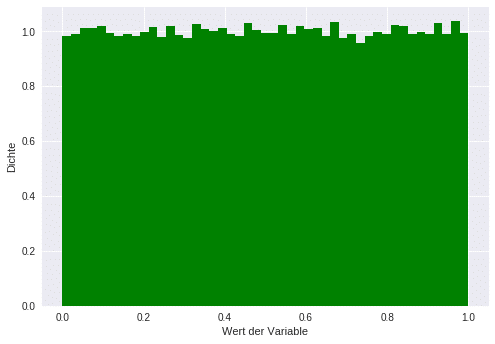
Anwendung
Ein typisches Beispiel für eine diskrete Gleichverteilung ist ein fairer Würfel, bei dem jede Seite mit der identischen Wahrscheinlichkeit von auftritt.
Ein Beispiel für eine stetige Gleichverteilung wäre die Wartezeit auf einen alle 10 Minuten verkehrenden Bus, wenn man zu einer zufälligen Zeit an der Bushaltestelle eintrifft.
Fazit – Was Sie von diesem Artikel mitnehmen sollten
| Verteilung | Anwendung | Dichtefunktion |
| Normalverteilung | Wichtigste Verteilung! Modellierung vieler natürlicher und statistischer Prozesse | 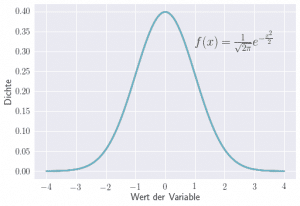 |
| t-Verteilung | Modellierung eigentlich normalverteilter Zufallsvariablen bei kleiner Stichprobengrösse | 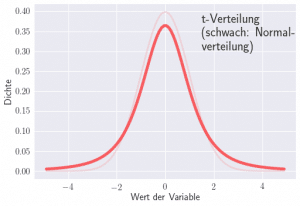 |
| Poisson-Verteilung | Modellierung von Zählgrössen | 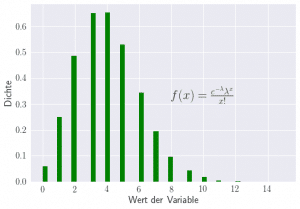 |
| Exponentialverteilung | Modellierung von Zeitintervallen | 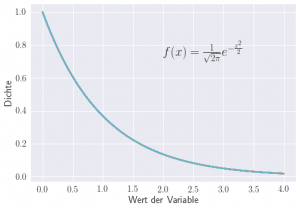 |
| Gleichverteilung | Modellierung von Prozessen, wo jeder Wert gleich wahrscheinlich ist. Existiert als stetige und diskrete Verteilung! | 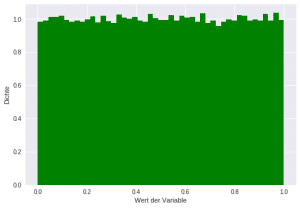 |
Zusammenfassend: Wann immer wir Dinge modellieren wollen, bei denen der Zufall im Spiel ist, sind Wahrscheinlichkeitsverteilungen ein unersetzliches Tool in der statistischen Werkzeugkiste. In diesem Blogeintrag wurden 5 zentrale Verteilungen besprochen – wir haben Ihnen unten einige Links zusammengestellt, die eine ausführliche Übersicht über mehr Verteilungen bieten. Falls Sie weiterführende Beratung zu diesem Thema oder anderen Themen wünschen, helfen wir ihnen gerne mit kompetenter Statistikberatung weiter!
Weiterführende Links
[1] Liste von Wahrscheinlichkeitsverteilungen