Einer der wichtigsten Kennzahlen für statistische Analysen ist sicherlich die Standardabweichung (Abkürzung Standardabweichung: SD oder s). Zahlreiche statistische Verfahren laufen letztendlich auf eine Analyse der Standardabweichung bzw. der Varianz (quadrierte Standardabweichung) hinaus. Die Varianzanalyse trägt die Varianz zum Beispiel bereits im Namen. Aber die Standardabweichung bildet auch für viele andere Verfahren den grundlegenden Baustein der Analyse. Ein grundlegendes Verständnis von Standardabweichung ist daher unerlässlich für jeden der mit Ergebnissen aus Datenanalysen zu tun hat. In diesem Artikel möchten wir Ihnen deshalb eine leicht verständliche Einführung für die Standardabweichung Interpretation präsentieren.
Wenn Sie Unterstützung bei der Auswertung oder Interpretation Ihrer Daten benötigen, helfen unsere Statistiker Ihnen gerne weiter. Kontaktieren Sie uns für eine kostenlose Beratung & ein unverbindliches Angebot.
Folgende Fragen werden in diesem Artikel beantwortet
- Was bedeutet Standardabweichung?
- Wie geht man für die Berechnung der Standardabweichung und Varianz vor?
- Wie kann ich die Standardabweichung sinnvoll interpretieren?
Standardabweichung Bedeutung – ein Praxisbeispiel
Grundsätzlich geben die Standardabweichung und die Varianz an, wie sehr die Daten vom Mittelwert abweichen. Anders gesagt drückt die Standardabweichung aus, wie stark sich die Datenpunkte voneinander unterscheiden. Zur Verdeutlichung ein Beispiel:
Ein Unternehmen möchte gerne wissen, wie zufrieden seine Kunden mit dem gekauften Produkt sind. In einer Kundebefragung beantworten Kunden unter anderem folgende Frage: „Mit welcher Wahrscheinlichkeit würden Sie unser Produkt weiterempfehlen?“

Was passiert, wenn die Standardabweichung null beträgt?
Nehmen wir einmal an, alle befragten Kunden hätten bei dieser Frage einen Wert von 7 angegeben. In diesem Fall wäre der Durchschnitt 7 und es gebe überhaupt keinen Unterschied zwischen den Datenpunkten; die Standardabweichung wäre 0. In solch einem Fall gäbe es tatsächlich keinen Ansatz für eine klassische statistische Analyse: Eines der wichtigsten Ziele von Statistik ist es Unterschiede zwischen Datenpunkten zu erklären und vorherzusagen. Wenn alle Kunden identisch sind gibt es keine Unterschiede die es zu erklären oder vorherzusagen gibt.
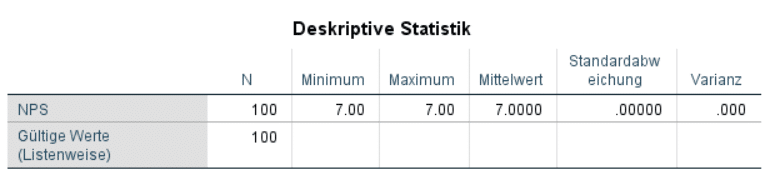
Ein solcher Fall ist natürlich extrem unwahrscheinlich. Selbst wenn alle Kunden die Dienstleistung normalerweise mit 7 bewerten würden, gibt es praktisch immer Messfehler. So bewerten manche Kunden das Produkt vielleicht etwas höher, weil Sie einen guten Tag hatten. Andere bewerten das Produkt etwas niedriger, weil Sie generell schwierig zufrieden zu stellen sind. Ein anderer Kunde hat sich einfach verklickt, und so weiter.
Standardabweichung bei annähender Normalverteilung
In diesem Fall werden die Daten um den Wert 7 herum liegen, der Durchschnitt wäre also 7. Alle Werte werden aber nicht identisch sein, manche Werte werden also unter 7 oder über 7 liegen. Wenn die Daten in etwa normal verteilt sind, werden die meisten Werte um den Mittelwert liegen. Werte mit geringer Abweichung vom Mittelwert werden häufiger vorkommen als Werte mit sehr starker Abweichung.
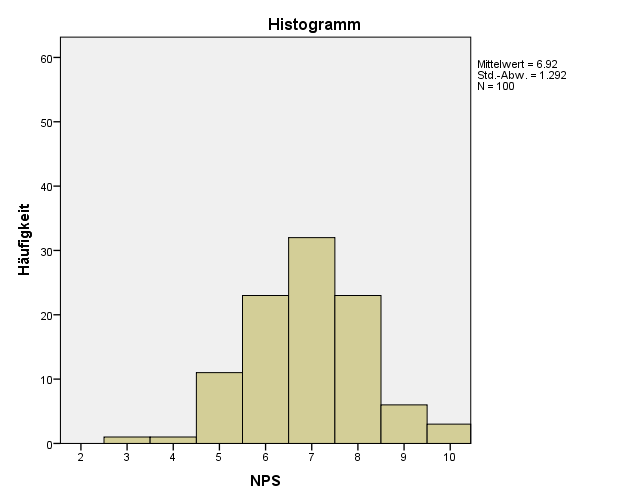
Wenn wir jetzt wissen wollen wie stark sich die Werte denn nun voneinander unterscheiden, ist die Standardabweichung eine äusserst praktische Grösse. Für die Standardabweichung müssen wir zunächst die Varianz berechnen.
Wünschen Sie ein massgeschneidertes und individuelles Coaching zum Verständnis und Anwendung statistischer Verfahren? Oder Sie benötigen Hilfe bei der Auswertung und Interpretation Ihrer Daten – beispielsweise durch professionelle Unterstützung beim Fragebogen auswerten?
Von der Statistik Nachhilfe bis hin zur Unterstützung durch eine vollständige statistische Auswertung: Unsere Experten helfen Ihnen schnell und kompetent weiter!
Von der Varianz zur Standardabweichung
Varianz ist der statistische Ausdruck für die Streuung der Daten. Die Varianz gibt also an wie weit sich die Daten im Schnitt vom Mittelwert unterscheiden. Um so grösser die Varianz umso weiter liegen die Daten vom Mittelwert entfernt.
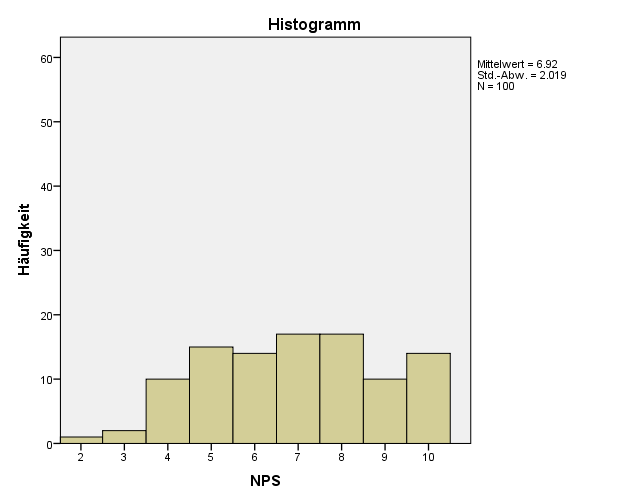
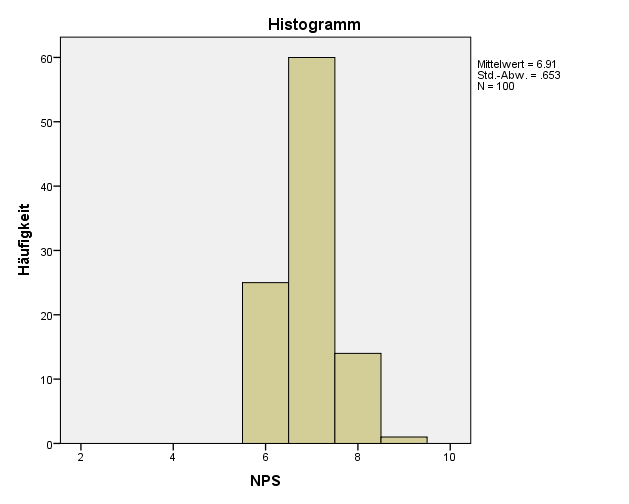
Die Abweichung vom Mittelwert können wir einfach ausdrücken als:
\(Abweichung=x-\bar{x}\)Wobei \(\bar{x}\) den Mittelwert darstellt.
Wenn der Wert nun kleiner als der Durchschnitt ist fällt die Abweichung negativ aus. Wir möchten aber, dass eine hohe Abweichung auch durch einen hohen Wert ausgedrückt wird. Für die Definition der Varianz verwendet man daher die quadrierten Abweichungen.
\(Quadrierte Abweichung= \left( x-\bar{x} \right) ^{2}\)Die Varianz der Population ist definiert als der Durchschnitt aller quadrierter Abweichungen:
\(Var \left( x \right) = \frac{ \sum _{i=1}^{n} \left( x_{i}-\bar{x} \right) ^{2}}{n}\)Das heisst wir rechnen für alle Werte zunächst die quadrierte Abweichung und bilden aus diesem dann den Durchschnitt. Eine Schätzung der Varianz mit einer kleinen Stichprobe unterschätzt diese allerdings. Um dafür zu korrigieren wird für die Berechnung der Stichprobenvarianz s2 für gewöhnlich durch n – 1 geteilt:
\(s^{2}= \frac{ \sum _{i=1}^{n} \left( x_{i}-\bar{x} \right) ^{2}}{n-1}\)Die Standardabweichung (Abkürzung Standardabweichung: SD oder s) ist einfach definiert als die Wurzel aus der Varianz:
\(s=\sqrt[]{s^{2}}= \sqrt[]{\frac{ \sum _{i=1}^{n} \left( x_{i}-\bar{x} \right) ^{2}}{n-1}}\)Was sagt dieser Wert jetzt aus? Wie wir Ihnen im nächsten Abschnitt zeigen hat die Standardabweichung einige sehr nützliche Eigenschaften. Diese machen die Standardabweichung Interpretation sehr einfach.
Interpretation Standardabweichung: Praktische Faustregeln
Wenn die Daten in einer Normalverteilung vorliegen, können Sie viele nützliche Informationen aus einer Standardabweichung Interpretation ablesen. Bei annähernd normal verteilten Daten liegen etwa 68% aller Daten innerhalb einer Standardabweichung vom Mittelwert. Etwa 95% liegen innerhalb von 2 Standardabweichung (genauer: 1,96) und 99,7% liegen innerhalb von 3 Standardabweichungen. Dies wird auch als 68-95-99,7 Regel bezeichnet. Bei normal verteilten Daten reicht also ein kurzer Blick auf den Mittelwert und die Standardabweichung um eine Vorstellung davon zu erhalten in welchen Bereich sich die meisten Daten bewegen.
Auch ein Konfidenzintervall lässt sich mit der Standardabweichung und dem Mittelwert schnell berechnen. Ein 95%-Konfidenzintervall hat einen kritischen z-Wert von 1,96. Der Mittelwert befindet sich also mit 95% Sicherheit zwischen \(M-1,96\ast\frac{SD}{\sqrt[]{n}}\) und \(M+1,96\ast\frac{SD}{\sqrt[]{n}}\).
Standardabweichung Interpretation in der Praxis
Zurück zu unserem Beispiel: Eine erste Analyse der Kundenbefragung ergab, dass die Daten annähernd normal verteilt sind. Eine deskriptive Analyse ergab folgende Kennzahlen:
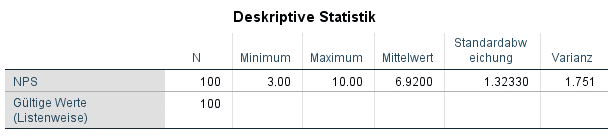
Aus dem Mittelwert und der Standardabweichung lässt sich mit der 68-95-99,7 Regel ermitteln, wie sich die Daten bei einer Normalverteilung ungefähr verteilen sollten (Abkürzung Mittelwert: M, Abkürzung Standardabweichung: SD).
| Anteil der Daten | Faustregel | Ungefährer Bereich |
| 68% | M +/- SD | 5,60 – 8,24 |
| 95% | M +/- (SD*2) | 4,27 – 9,57 |
| 99,7% | M +/- (SD*3) | 2,95 – 10 |
Beachten Sie bei der obigen Tabelle, dass 99,7% der Daten eigentlich zwischen 2,95 – 10,89 liegen müssten, 10 aber den möglichen Maximalwert der Skala darstellt.
Um genauer abschätzen zu können in welchem Bereich die Kundenzufriedenheit vermutlich liegt soll ein 95%-Konfidenzintervall ermittelt werden. Dies kann natürlich einfach in SPSS erledigt werden, ist aber auch per Hand schnell erledigt:
\(95\%KI=M \pm 1,96\ast\frac{SD}{\sqrt[]{n}}=6,92 \pm 1,96\ast\frac{1,32}{\sqrt[]{100}}=6,92 \pm 0,26= \left[ 6,66;7,18 \right]\)Der Mittelwert liegt also mit 95% Sicherheit zwischen 6,7 und 7,2. Eigentlich wird ein durchschnittlicher Wert von 8 angestrebt. Eine anschliessende Studie soll klären welchen Faktor zu mehr Zufriedenheit beitragen könnten. Dies könnte etwa durch eine ANOVA oder Regressionsanalyse geschehen.
Zusammenfassung: Interpretation Standardabweichung einfach gemacht
In diesem Artikel haben wir Ihnen eine kurze Einleitung zur Standardabweichung Interpretation gegeben. Die Standardabweichung ist eine zentrale Kennzahl der Statistik und bildet den Grundbaustein für viele wichtige statistischen Verfahren. Aber allein in Kombination mit dem Mittelwert ist die Standardabweichung Bedeutung bereits sehr aufschlussreich, insbesondere bei normal verteilten Daten.
Im Anschluss an eine erste Analyse des Mittelwerts und der Standardabweichung bietet sich oft eine vertiefende Analyse der Daten mit fortgeschrittenen Verfahren an. Wenn Sie hier Beratung über das weitere Vorgehen wünschen stehen unsere Experten von Novustat Ihnen gerne zur Seite.
Weiterführende Quellen:
Wissenschafts-Thurm: Grundlagen zur Standardabweichung
Eräuterung zum Unterschied zwischen Standardabweichung und Standardfehler