In der inferenziellen Statistik (auch: schliessende Statistik) werden Hypothesen auf eine bestimmte Verteilung, auf einen Zusammenhang und auf einen signifikanten Unterschied innerhalb der betrachteten Merkmale getestet. Eine wesentliche Frage in diesem Zusammenhang betrifft den Test auf Normalverteilung. Dies gilt insbesondere für sogenannte parametrische Verfahren. In diesem Artikel werden zwei statistische Testverfahren in SPSS zur Überprüfung der Normalverteilung vorgestellt: der Kolmogorov-Smirnov Test (KS-Test) und der Shapiro Wilk Test.
Sollten Sie Unterstützung bei Ihrer SPSS Auswertung benötigen, helfen unsere Statistiker Ihnen gerne weiter!
Kolmogorov-Smirnov Test auf Normalverteilung in SPSS
Der Kolmogorov-Smirnov Anpassungstest (KS-Test in SPSS) testet die Annahme der Normalverteilung, SPSS verlangt hier ein metrisch (kardinal) skaliertes Merkmal. Im Rahmen einer statistischen Auswertung entscheidet der Ausgang darüber, ob die Stichprobe im weiteren Verlauf parametrisch oder nicht-parametrisch zu testen Ist.
Nachfolgend wird zunächst der mathematische Hintergrund erläutert, bevor der KS-Test SPSS nutzend anhand zweier Beispiele erläutert wird.
Sie brauchen Hilfe bei der statistischen Analyse in SPSS? Nutzen Sie unsere professionelle Unterstützung bei der SPSS Auswertung – unsere Experten helfen Ihnen jederzeit weiter!
Der KS-Test – der mathematische Hintergrund
Der KS-Test gehört, wie alle Anpassungstests, zur Gruppe der nicht-parametrischen Testverfahren, da er keinerlei Voraussetzungen an die Verteilung der Merkmale richtet.
Die Quantile der Verteilung können für bis zu 30 Elemente der Kolmogorov-Tabelle entnommen werden, ab Werten darüber werden sie durch die Normalverteilung approximiert.
Die Teststatistik des KS-Tests in SPSS entspricht der grössten Abweichung der empirischen Dichte des Merkmals von der Referenzverteilung, auf die getestet wird. Überschreitet dieser Wert das entsprechende Quantil in der Tabelle, so muss die Annahme der Normalverteilung (in der Nullhypothese) verworfen werden.
Aufgrund seiner einfachen Berechnung wird der KS-Test in SPSS oftmals dem Chi Quadrat Test vorgezogen.
Der KS-Test auf Normalverteilung – SPSS sinnvoll nutzen
Um für den KS-Test SPSS zu nutzen geht man zu den nicht-parametrischen Tests, hier kann er auf zwei Wegen durchgeführt werden und setzt lediglich ein kardinal skaliertes Merkmal voraus.
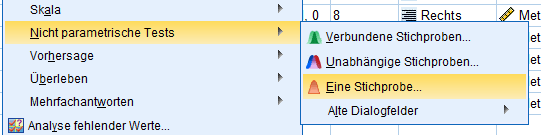
Über den Auswahldialog zum Testen einer Stichprobe ist der KS-Test in SPSS als standardisierter Anpassungstest eingestellt unter dem Pfad: „Analysieren → Nicht parametrische Tests → Eine Stichprobe“. Nach der Auswahl des zu testenden metrischen Merkmals liefert SPSS eine vollständige Auswertung.
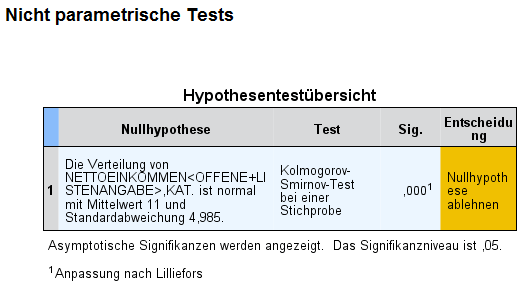
Da die Signifikanz unter 5% liegt, ist die Nullhypothese „Das Nettoeinkommen ist normalverteilt“ zu verwerfen.
Alternativ findet sich der KS-Test in SPSS unter den alten Dialogfeldern im Pfad: „Analysieren → Nicht parametrische Tests → Alte Dialogfelder → K-S bei einer Stichprobe“
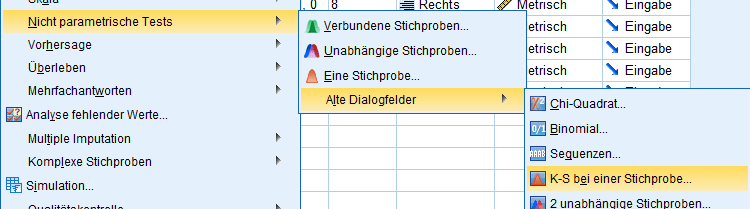
Auf diesem Weg lässt sich neben der Normalverteilung SPSS verwendend auch die Auswahl weiterer Referenzverteilungen (Gleichverteilung, Poisson-, Exponentiellverteilung) anwählen. Wie bereits der Test oben ergab, ist das Nettoeinkommen nicht normalverteilt, da die Signifikanz unter 5% liegt.
Der Shapiro Wilk Test auf Normalverteilung in SPSS
Für den Shapiro Wilk Test SPSS verwendend wird die Hypothese der Normalverteilung für ein metrisch (kardinal) skaliertes Merkmal geprüft, die auch bei geringem Stichprobenumfang vergleichsweise aussagekräftig ist.
Nachfolgend wird zunächst der mathematische Hintergrund erläutert, bevor der Shapiro Wilk Test SPSS nutzend anhand eines Beispiels erläutert wird.
Der Shapiro Wilk Test – der mathematische Hintergrund
Im Gegensatz zum Chi Quadrat Test und dem KS-Test ist der Shapiro Wilk Test auf die Normalverteilung geeicht. Dies ermöglicht auch bei geringerem Stichprobenumfang (weniger als 100 Befragte) einen aussagekräftigen Test, schränkt die Anwendungsmöglichkeiten dagegen ein.
Die Shapiro Wilk Statistik entspricht dem Quotienten aus der „erwarteten“ Varianz der Referenzverteilung und dem Schätzer der tatsächlichen Varianz in der Stichprobe
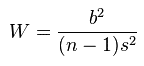
.
Der kritische Wert für den Signifikanztest wird, da es sich um eine Abschätzung quadratischer Fehler handelt, der Tabelle zur Fisher-Verteilung (bzw. f-Test SPSS) entnommen.
Der Shapiro Wilk Test – SPSS sinnvoll nutzen
Will man für den Shapiro Wilk Test SPSS verwendet, kann man diesen im Gegensatz zu anderen Anpassungstests nicht direkt wählen, da er zur Berechnung der Statistik explorative Methoden verwendet.
Die Durchführung erfolgt entsprechend über den Pfad: „Analysieren → Deskriptive Statistiken → Explorative Datenanalyse“.
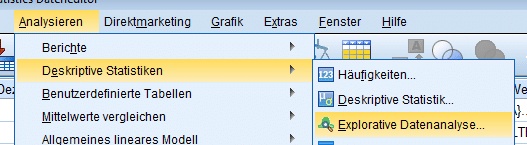
Hier wird aus der Liste das zu untersuchende metrische Merkmal ausgewählt – ergänzend ist anzumerken, dass zudem Diagramme und/oder Statistiken ausgegeben werden, da die Varianz der Normalverteilung SPSS nutzend anhand des QQ-Plots bestimmt wird.
Nach einem Klick auf den Button „Diagramme“ können ein Histogramms und ein Boxplot zur Veranschaulichung ausgewählt werden, für den Shapiro-Wilk Test sind sie aber nicht zwingend notwendig. Wichtig ist, sich per Klick auf „ Normalverteilungsdiagramm mit Tests“ sich diese ausgeben zu lassen.
Nach zweimaliger Bestätigung werden sowohl der KS-Test als auch der Shapiro Wilk Test ausgeführt. Nachfolgende Tabelle zeigt die Ergebnisse des KS-Test SPSS als auch des Shapiro Wilk Test SPSS:
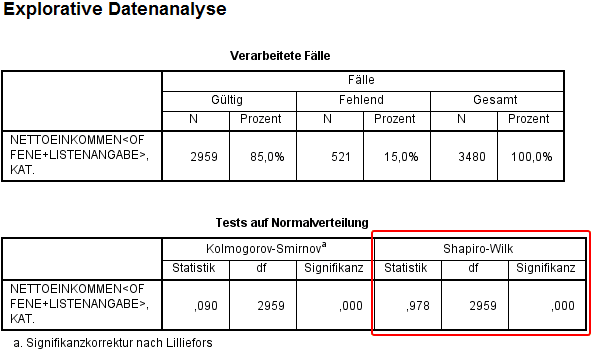
Da im gewählten Beispiel mehr als 2000 Personen befragt wurden, gelangen der KS-Test und der Shapiro Wilk Test zum gleichen Ergebnis. Beide Tests verwerfen die Nullhypothese und gehen davon aus, dass eine Normalverteilung nicht angenommen werden kann. Kämen im Falle einer kleinen Stichprobe die beiden Tests zu unterschiedlichen Ergebnissen, empfiehlt es sich dem Shapiro Wilk Test aufgrund der genannten höheren Teststärke zu folgen.
Häufig gestellte Fragen
Weiterführende Links
Anderson-Darling and Shapiro-Wilk tests