In der inferenziellen Statistik (auch: schliessende Statistik) werden Hypothesen auf eine bestimmte Verteilung, auf einen Zusammenhang und auf einen signifikanten Unterschied innerhalb der betrachteten Merkmale getestet. Der Test von Chi Quadrat SPSS anwendend kommt für zwei dieser Hypothesentests in Frage. Einerseits ermöglicht er den Test einer metrischen Variable auf eine bestimmte Verteilung (Verteilungstest oder Anpassungstest genannt), d.h zum Beispiel einen Test auf Normalverteilung. Andererseits dient er dem Test auf Unabhängigkeit zweier beliebig skalierter Merkmale (Unabhängigkeitstest). Nachfolgend erläutern wir zunächst den mathematischen Hintergrund der Statistik-Auswertung mit Chi Quadrat. Daraufhin zeigen wir anhand zweier Beispiele, wie man die Berechnung des Chi Quadrat Tests in SPSS vornimmt.
Sollten Sie Unterstützung bei Ihrer SPSS Auswertung benötigen, helfen unsere Statistiker Ihnen gerne weiter. Kontaktieren Sie uns für eine kostenlose Beratung & ein unverbindliches Angebot!
Der Chi Quadrat Test – der mathematische Hintergrund
Der Chi Quadrat Test gehört zur Gruppe der Likelihood-Quotienten Tests. Dieser Test vergleicht die beobachteten Häufigkeiten in der beobachteten Verteilung mit den – im Rahmen der in der Nullhypothese angenommenen Gleichverteilung – erwarteten Häufigkeiten.
Die Abweichungen von beobachteten und erwarteten Häufigkeiten werden quadriert, als gewichteter Quotient aufsummiert und mit den Quantilen der Chi Quadrat Verteilungstabelle verglichen. Diese Quantile werden auch als kritischer Wert bezeichnet und entsprechen dem gewählten Signifikanzniveau.
Ist der Wert der Chi Quadrat Teststatistik grösser als der kritische Wert aus der Verteilungstabelle, so wird die Nullhypothese zugunsten der Alternativhypothese verworfen und es lässt sich nicht von einer Gleichverteilung der Daten sprechen.
Sie möchten einen Chi Quadrat Test in SPSS anwenden, benötigen aber Unterstützung bei der Durchführung oder Interpretation der Daten? Dann nutzen auch Sie unsere massgeschneiderte SPSS Hilfe! Unsere Experten sind vertraut mit der Vielzahl an statistischen Verfahren in SPSS und helfen Ihnen schnell und kompetent weiter.
Chi Quadrat SPSS – Verteilungstest
Der Verteilungstest (oder auch: Anpassungstest) für Chi Quadrat SPSS nutzend findet sich unter dem Pfad: „Analysieren → Nicht parametrische Tests → Alte Dialogfelder → Chi-Quadrat“ und erstellt für eine metrisch (kardinal) skalierte Variable einen Test auf Normalverteilung. SPSS rechnet standardmässig mit einem 95% Signifikanzniveau.
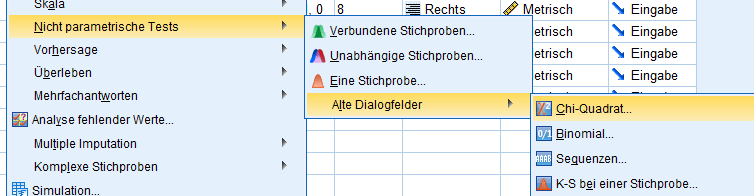
Nach der Bestätigung wird das zu testende metrische Merkmal aus der Liste ausgewählt und der Test durchgeführt. Die Signifikanz (p-Wert) kann der ausgegebenen Tabelle entnommen werden – da diese unter 5% liegt, muss die Nullhypothese verworfen und die Normalverteilung kann nicht angenommen werden.

Chi Quadrat SPSS – Unabhängigkeitstest
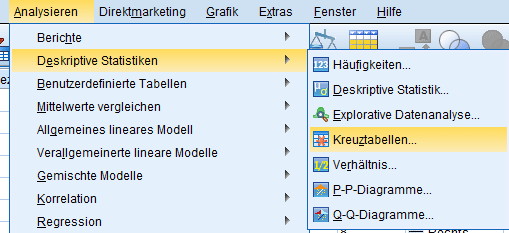
Der Unabhängigkeitstest für Chi Quadrat SPSS anwendend ist unter dem Pfad: „Analysieren → Deskriptive Statistiken → Kreuztabellen“ zu finden und testet zwei (nominale und/oder ordinale) Merkmale auf Unabhängigkeit.
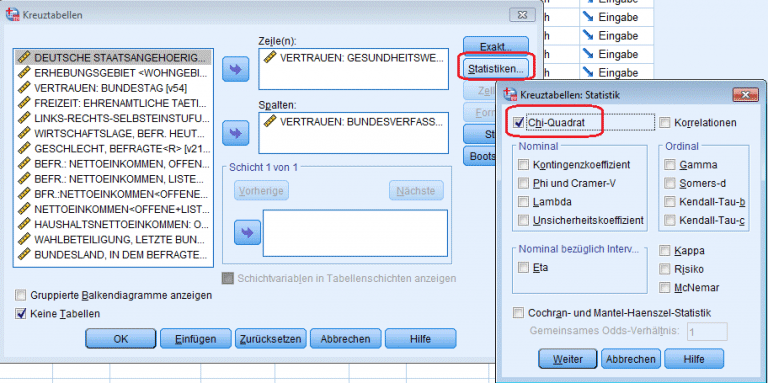
Nachdem die zu untersuchenden Merkmale aus der Liste ausgewählt wurden, ist unter „Statistiken“ das „Chi-Quadrat“ Mass auszuwählen.
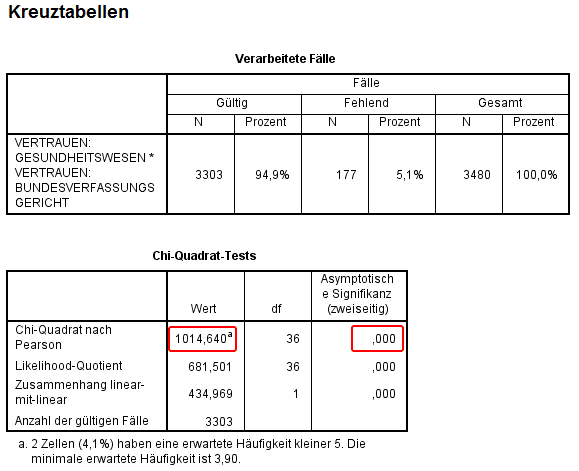
Nach zweimaliger Bestätigung wird Chi Quadrat in SPSS getestet und der zweiten Tabelle können den Chi Quadrat Wert sowie die Signifikanz entnommen werden. Die Signifikanz (p-Wert) liegt in diesem Beispiel unter 5%. Somit wird die Nullhypothese der Unabhängigkeit verworfen und ein signifikanter Zusammenhang (Abhängigkeit) zwischen beiden untersuchten Variablen angenommen.