Der Begriff „Signifikanz“ hat in der Statistik eine wichtige Bedeutung. Die Signifikanz misst, ob eine gemachte Beobachtung auch tatsächlich etwas zu bedeuten hat oder zufällig entstanden sein könnte. Somit sollte die Signifikanz Statistik-Interessierten ein wichtiger Begriff sein.
Folgende Fragen werden in diesem Text geklärt:
- Was bedeutet der Begriff „Signifikanz“ in der Statistik?
- Wovon hängt die Signifikanz der Statistik ab?
- Wie berechnet man die statistische Signifikanz?
- Wo finde ich weitere Informationen zu Signifikanz- Statistik?
Sollten Sie Unterstützung bei der Erhebung oder Analyse von Daten benötigen, helfen unsere Statistiker Ihnen gerne weiter. Nutzen Sie einfach unser Kontaktformular für eine kostenlose Beratung & ein unverbindliches Angebot – oder rufen Sie uns an.
Was bedeutet der Begriff „Signifikanz“ in der Statistik?
In der Statistik vergleicht man oft zwei Gruppen von Daten, Personen oder anderen Objekten miteinander hinsichtlich einer Eigenschaft. Beispielsweise vergleicht man zwei Gruppen von Mäusen, wobei die einen ein Medikament erhalten haben und die anderen als Kontrollgruppe ohne Behandlung blieben. Beobachtet man einen Unterschied zwischen den beiden Gruppen, dann stellt sich die Frage, ob dieser etwas zu bedeuten hat. Hat das Medikament tatsächlich geholfen? Der beobachtete Unterschied könnte ja auch zufällig entstanden sein, z.B. durch eine unglückliche Auswahl der betrachteten Stichprobe aus der Grundgesamtheit, oder weil zwei Gruppen nie wirklich identisch miteinander sind. So könnte man zufällig für die Kontrollgruppe die Mäuse mit schlechterer Gesundheit gewählt haben und für die Gruppe, die das Medikament erhielt, diejenigen, die sowieso gesünder und robuster sind.
Die statistische Signifikanz misst, wie gross die Wahrscheinlichkeit dafür ist, dass der beobachtete Unterschied nicht zufällig entstanden ist und tatsächlich etwas zu bedeuten hat, also auch in der Grundgesamtheit ein Unterschied besteht.
Wovon hängt die Signifikanz der Statistik ab?
Die statistische Signifikanz hängt von vielen Grössen ab. Beispielsweise wird sie durch die Stichprobengrösse beeinflusst. Hat man nur wenige Exemplare untersucht, dann ist es wahrscheinlicher, dass diese nicht die Grundgesamtheit repräsentieren und zufällige Unterschiede aufweisen. Ist eine Stichprobe gross genug, um zufällige Unterschiede relativ sicher auszuschliessen, spricht man von einer repräsentativen Stichprobe. Eine wichtige Rolle spielt auch die Varianz der beobachteten Grösse innerhalb der Gruppe. Sind beispielsweise die behandelten Mäuse alle innerhalb von zwei Tagen wieder gesund geworden und die Kontrollgruppe alle genau nach sieben Tagen, ist der Unterschied deutlich. Hat es aber in beiden Gruppen grosse Unterschiede in der Heilungsdauer gegeben, wird es schon schwieriger zu beurteilen, ob der beobachtete Unterschied durch das Medikament und nicht durch andere Faktoren verursacht wurde.
Wie berechnet man die statistische Signifikanz?
Üblicherweise kennt man die Varianz der Variablen in der Grundgesamtheit nicht und auch nicht innerhalb der beiden Gruppen. Das erschwert die Berechnung der statistischen Signifikanz. Man behilft sich hier jedoch mit einem Trick: Man behauptet erst das Gegenteil von dem, was man zeigen möchte, und dann widerlegt man es. Im Mäuse-Beispiel würde man also behaupten, dass die beiden Gruppen die gleiche Heilungschance hatten, also im Schnitt dieselbe mittlere Heilungsdauer und die Verteilung der Dauern habe dieselbe Varianz. Durch diese Annahmen über die Verteilung werden statistische Verfahren anwendbar, die man nicht hätte einsetzen können, wenn beide Verteilungen völlig verschieden und unbekannt wären.
Als Gegenhypothese könnte man auch formulieren: „Die Heilungsdauer für die nicht behandelten Mäuse ist gleich oder kleiner als für die Mäuse, die das Medikament erhalten haben.“
Die Forschungshypothese, die man eigentlich untersuchen will, nennt man üblicherweise H1 oder auch Alternativhypothese. Die zu verwerfende Gegenhypothese heisst Nullhypothese H0.
Es gibt nun vier Möglichkeiten:
| H0 ist richtig | H0 ist falsch. H1 ist richtig | |
| H0 wird als richtig angenommen. | Dies wäre richtig. (Wahrscheinlichkeit 1-α) | Dies wäre ein Fehler 2. Art. (Wahrscheinlichkeit β) |
| H0 wird als falsch verworfen. | Dies wäre ein Fehler 1. Art. (Wahrscheinlichkeit α) | Dies wäre richtig. (Wahrscheinlichkeit 1-β) |
Auch wenn man anhand von Daten aus einer Stichprobe nicht wirklich beweisen kann, ob die Nullhypothese H0 richtig oder falsch ist, kann man doch mit statistischen Hypothesentests die Grösse des α-Fehlers und des β-Fehlers berechnen. Je kleiner diese Fehler, umso sicherer kann man sein, die richtige Schlussfolgerung aus den Daten zu ziehen. Der Fehler β ist umso kleiner, je grösser α, was eine völlige Sicherheit unmöglich macht.
Bei vielen zufällig verteilten Variablen kann man eine Gauss-Verteilung (Normalverteilung) annehmen wie im folgenden Bild. Der Wert μ sei der Erwartungswert und die Standardabweichung σ misst die Breite der Verteilung. Dabei findet man im Intervall [μ – σ, μ + σ] insgesamt 68,27% aller Messwerte, innerhalb von [μ – 2σ, μ + 2σ] 95,45% und in [μ – 3σ, μ + 6σ] 99,73%.
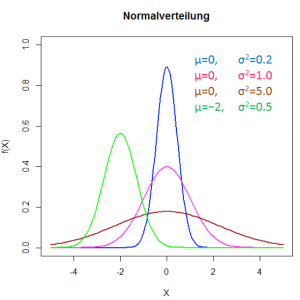
Hier kann man gut verstehen: Je breiter die Verteilung, d.h. je grösser σ, umso grösser der Bereich, in dem sich zwei nebeneinander liegende Gaussverteilungen überschneiden. Umso höher ist auch die Wahrscheinlichkeit, dass die zugehörigen Stichproben gleiche Werte enthalten, obwohl sie zu zwei verschiedenen Verteilungen gehören. Umso wahrscheinlicher wird ein Fehler 1. Art und umso grösser α. Auch der Unterschied ihrer beiden Mittelwerte spielt eine Rolle.
Der Signifikanztest besteht nun darin, den Fehler 1. Art zu berechnen. Dazu geht man so vor:
- Man nimmt an, die Nullhypothese H0 sei richtig, z.B. die beiden Stichproben seien gleich.
- Man macht Annahmen über die Wahrscheinlichkeitsverteilung der Variablen und schätzt deren Erwartungswert und die Standardabweichung anhand der Messwerte.
- Man berechnet unter diesen Annahmen die Wahrscheinlichkeit α, dass obwohl H0 richtig ist, trotzdem zufällig in den Messwerten der gefundene Unterschied zwischen den Gruppen beobachtet wird. Dazu nimmt man die Wahrscheinlichkeitsverteilung zu Hilfe. Bei den gängigsten Wahrscheinlichkeitsverteilungen kann man in einer Tabelle nachschlagen, wie gross die Wahrscheinlichkeit ist, dass die Prüfvariable in einem bestimmten Bereich liegt, z.B. der Unterschied der beiden Mittelwerte zweier gleicher Proben sich um einen bestimmten Wert unterscheiden. Für gaussverteilte Stichproben mit bekannter Standardabweichung verwendet man die Normalverteilung, für solche mit unbekannter Standardabweichung den Student- oder t-Test.
- Man vergleicht α mit dem Wert, den man sich als Grenzwert gesetzt hat. Üblich sind Werte für das Signifikanzniveau von 5% oder 1%. Liegt die Fehlerwahrscheinlichkeit α darunter, dann ist das Ergebnis statistisch signifikant mit einer Wahrscheinlichkeit von 95% oder 99%.
- 1-β bezeichnet man als die Teststärke (statistical power) oder Sensitivität. Die Wahrscheinlichkeit β ist von Hand nur schwer zu berechnen. Werkzeuge zu dessen Berechnung sind unten angegeben. Ist β zu klein, dann sollte die Stichprobengrösse erhöht werden.
Häufig gestellte Fragen
Wo finde ich weitere Informationen zu Signifikanz- Statistik?
Vorgehensweisen beim Hypothesentest
Werkzeuge für die Berechnung der Teststärke:
Plug-in für R
Online-Tool für die Berechnung