In der inferenziellen Statistik (auch: schliessende Statistik) werden Hypothesen auf eine bestimmte Verteilung, auf einen Zusammenhang und auf einen signifikanten Unterschied innerhalb der betrachteten Merkmale getestet.
Die Varianzanalyse, auch ANOVA SPSS genannt (Analysis of Variance), testet den Einfluss einer unabhängigen kategorialen Variable (mit nominalem Skalenniveau) auf ein abhängiges metrisch (kardinal) skaliertes Merkmal. Da für das kardinale Merkmal die empirische Verteilung ermittelt werden kann, zählt die Varianzanalyse / ANOVA in SPSS zu den parametrischen Testverfahren.
Nachfolgend wird zunächst der mathematische Hintergrund des Verfahrens erläutert, bevor der Ablauf einer Varianzanalyse-SPSS anhand eines Beispiels gezeigt wird.
Sollten Sie Unterstützung bei Ihrer Auswertung mit SPSS benötigen, helfen unsere Statistiker Ihnen gerne weiter. Nutzen Sie einfach unser Kontaktformular für eine kostenlose Beratung & ein unverbindliches Angebot – oder rufen Sie uns an.
Die Varianzanalyse – der mathematische Hintergrund
Zunächst sei daran erinnert, dass in der deskriptiven Statistik drei Messniveaus unterschieden werden: nominal, ordinal und metrisch (kardinal).
Während für das metrisch skalierte Merkmal die empirische Varianz anhand der Formel
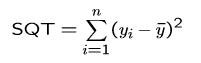
ermittelt werden kann, unterteilt das unabhängige Merkmal die Stichprobe in Gruppen – für diese kann jeweils die gruppeninterne Varianz ermittelt werden.
So lässt sich die Berechnung der gesamten Varianz wie folgt zerlegen: SQT = SQE + SQR
SQR entspricht der residualen Varianz innerhalb der Gruppen, SQE der externen Varianz zwischen den Gruppen, die erst durch die Gruppenbildung auftritt.
Im Rahmen der ANOVA SPSS werden beide Grössen ermittelt und daraus die Kenngrösse
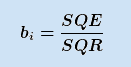
abgeleitet – diese gibt die Stärke des Einflusses der unabhängigen Variablen auf die abhängige Variable an.
Die Varianzanalyse SPSS
Um für die Varianzanalyse SPSS zu nutzen, wird der Pfad: „Analysieren → Mittelwerte vergleichen → Einfaktorielle Varianzanalyse“ gewählt.
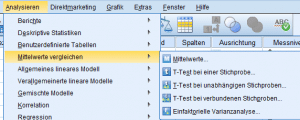
Nach der Bestätigung werden das metrische abhängige Merkmal und das nominal (oder ordinal) skalierte unabhängige Merkmal (Faktor) aus der Liste gewählt, hier konkret das Einkommen als abhängige Variable und die Zufriedenheit mit dem Job als Faktorvariable.
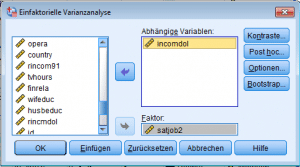
In der ersten Spalte der Ausgabetabelle der Varianzanalyse SPSS finden sich die erklärten Quadratsummen SQE, SQR und SQT, in der letzten Spalte die Signifikanz.
Da der Wert unterhalb von 5% liegt, kann die Nullhypothese verworfen und damit angenommen werden, dass die Zufriedenheit mit dem Job einen signifikanten Einfluss auf das jährliche Einkommen hat.
Häufig gestellte Fragen
Weiterführende Links
Uni Würzburg – Varianzanalyse – ANOVA
Uni Zürich – Einfaktorielle Varianzanalyse (ohne Messwiederholung)