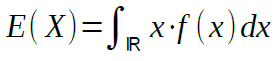Die univariate Datenanalyse beschreibt Methoden zur Auswertung eines singulär betrachteten Samples, dabei orientiert sie sich an den aus der Wahrscheinlichkeitstheorie bekannten Konzepten.
Im Folgenden werden zunächst die theoretischen Grundlagen erläutert bevor die Datenanalyse in SPSS erläutert wird. Anhand eines Beispiels werden die Methoden zur Datenanalyse vorgestellt und die gewonnenen Resultate interpretiert.
Sollten Sie Unterstützung bei einer SPSS Auswertung benötigen, helfen unsere Statistiker Ihnen gerne weiter. Nutzen Sie einfach unser Kontaktformular für eine kostenlose Beratung & ein unverbindliches Angebot – oder rufen Sie uns an.
Lage und Streuung
Das mathematische Konzept, auf dem die statistische Datenanalyse aufbaut, besteht aus Zufallsvariablen und ihren wahrscheinlichen Verteilungen. Eine Wahrscheinlichkeitsverteilung gibt an, mit welcher Wahrscheinlichkeit ein bestimmter Wert (höchstens) auftritt.
Entscheidende Grössen einer Wahrscheinlichkeitsverteilung sind der Erwartungswert
und die Standardabweichung
![]() .
.
f(x) ist dabei die Dichte der Verteilung, d.h. jene Fläche bzw. das Intervall, in dem die zu berechnende Zufallsvariable liegt.
Der Erwartungswert gibt den mittleren Bereich an um das die Verteilung streut – bei symmetrischen Verteilungen (Normalverteilung, Binomialverteilung) ist dieser Wert in der Mitte des Wertebereichs. Er wird daher auch theoretischer Mittelwert genannt.
Die Standardabweichung gibt – wie der Name sagt – die Stärke der Streuung vom Erwartungswert (auch Dispersion genannt) an.
Da beide Kennzahlen ein rein theoretisches Konstrukt sind, dem eine (theoretische) Wahrscheinlichkeitsverteilung zu Grunde liegt, findet in der univariaten Datenanalyse in SPSS die auf der empirischen, also beobachteten, Häufigkeitsverteilung basierende Berechnung Anwendung.
Skalierung von Daten
Zunächst gilt zu beachten, dass in der deskriptiven Statistik drei Skalenniveaus unterschieden werden. Da SPSS auf Basis numerisch erfasster Daten auswertet, ist bei der Auswertung auf die Skalierung der Daten zu achten.
- Nominale Skalen – in diese Gruppen fallen alle Merkmale, deren Ausprägungen durch nur Worte ausgedrückt werden und zwischen denen keine Rangfolge besteht (Geschlecht, Haarfarbe).
Die numerische Repräsentation dient hier nur der Zuordenbarkeit (z.B. ‚1‘ = männlich; ‚2‘ = weiblich). - Ordinale Skalen – in diese Gruppe fallen Merkmale, bei denen zwischen den verschiedenen Ausprägungen eine eindeutige Rangfolge existiert (Grad des Vertrauens, Steuerklasse, Altersgruppen).
Eine numerische Codierung erfasst die Rangfolge und ermöglicht eine Reihung. - Metrische (oder: kardinale) Skalen – diese Gruppe umfasst alle Merkmale, deren Ausprägungen numerische Werte sind (Alter, Einkommen, Temperatur) und deren Abstände berechenbar sind; eine Codierung ist damit nicht notwendig.
Mittelwerte in SPSS
Die Berechnung von Mittelwerten in SPSS kann über mehrere Wege erfolgen, zwei davon werden hier erläutert – zum einen über den Pfad: „Analysieren → Mittelwerte vergleichen → Mittelwerte“
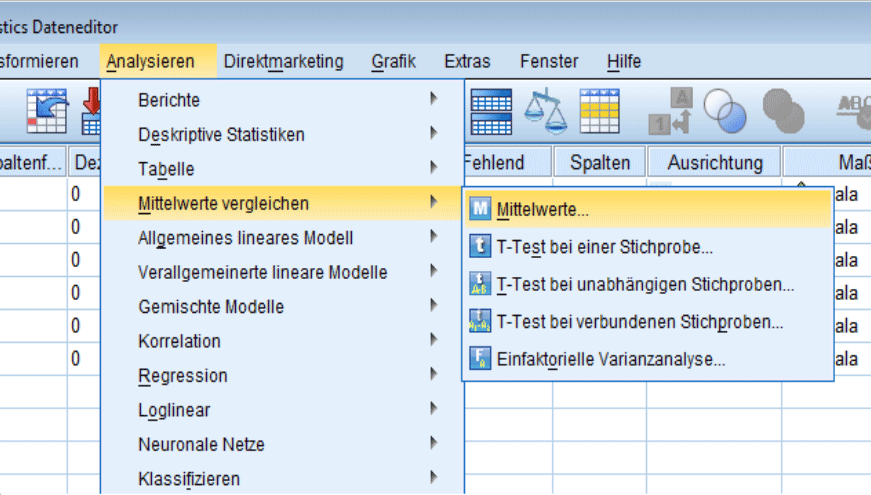
Im nächsten Schritt wird die zu untersuchende Variable und unter „Optionen“ die zu bestimmende Kennzahl ausgewählt.
Der zweite übersichtlichere Weg findet sich unter: „Analysieren → deskriptive Statistiken → Häufigkeiten
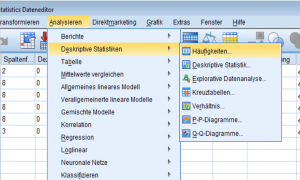
Hier wird zunächst wieder die zu untersuchende Variable ausgewählt, danach finden sich unter „Statistiken“ nach Funktionen geordnet sämtliche Lagemasse und Streuungsparameter
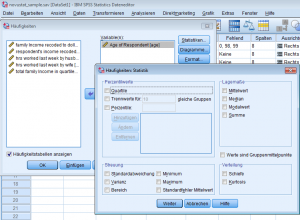
Interpretation der Kennzahlen
Entsprechend der Skalenniveaus gibt es drei Lageparameter, die SPSS stets berechnen kann, allerdings ist eine Interpretation nicht immer sinnvoll.
- Modalwert – dies ist jener Wert, der in der Stichprobe am Häufigsten vorkommt, er lässt sich für alle genannten Skalenniveaus bestimmen. Bei mehreren Maxima ist er nicht eindeutig interpretierbar.
- Median – in einer geordneten Stichprobe liegt dieser Wert genau in der Mitte, das heisst 50% der Werte liegen unterhalb und 50% oberhalb des Medians. Der Median ist damit gut geeignet für schiefe Daten, d.h. wenig anfällig für Ausreisser und Extremwerte. Das setzt zur Ermittlung und Interpretation eine ordinale oder metrische (kardinale) Skala voraus.
- Mittelwert – er ist das gewichtete Mittel, der (arithmetische) Durchschnitt; in die Berechnung werden alle Einzelwerte einbezogen. Der (arithmetische) Mittelwert lässt sich sinnvoll nur für metrische (kardinale) Skalen berechnen und interpretieren.
Die Bestimmung der Mittelwerte in SPSS
Wie bereits beschrieben, können die Lageparameter in SPSS über mehrere Pfade ermittelt werden. Das Resultat ist eine tabellarische Darstellung der Kennzahlen, wie der nachfolgende SPSS-Output zeigt:

Da die Variable Geschlecht nominal skaliert ist (mit der Codierung ‚ 1‘ = männlich und ‚2‘ = weiblich), hat die Codierung lediglich eine Kategorien erklärende Funktion. Weder Median noch Mittelwert bieten sinnvolle Interpretation, da die Codierung der Variable Geschlecht keine natürliche Rangfolge besitzt.
Lediglich der Modalwert lässt sich hier sinnvoll interpretieren, die (absolute) Mehrheit der Befragten ist weiblich.
Das Vertrauen in das Gesundheitssystem ist im Gegensatz dazu ordinal skaliert auf einer Skala von 1 (volles Vertrauen) bis 7 (kein Vertrauen). Hier lassen sich also Modalwert und Median interpretieren. Die meisten Befragten gaben demnach an, dem Gesundheitssystem eher wenig (Modalwert = 5) zu vertrauen. Der Median von 5 sagt zudem aus, dass 50% der Befragten dem Gesundheitssystem noch weniger vertrauen und die anderen 50% dem System mehr vertrauen. Der Mittelwert von 4,95 lässt sich nicht sinnvoll interpretieren, da die Abstände zwischen den einzelnen Werten nicht exakt bestimmt werden können (z.B. lässt sich eine Bewertung mit ‘2’ im Vergleich zu ‘4’ nicht als ‘doppelt so hohes Vertrauen’ interpretieren).
Beim metrisch (kardinal) skalierten Nettoeinkommen lassen sich hingegen alle in SPSS ermittelten Lageparameter sinnvoll interpretieren. Die meisten Befragten gaben an, 2000 Euro zu verdienen (Modalwert = 2000), 50% der Befragten verdienen unter 1200 Euro und 50% verdienen mehr als 1200 Euro. (Median = 1200). Der (arithmetische) Mittelwert von 1484,92 gibt an, dass alle Befragten in Durchschnitt 1484,92 Euro verdienen. Wenn es in den Einzeldaten Extremwerte gibt (z.B wenige hohe Einkommen), dann zeigt sich der Median als der aussagekräftigere Lageparameter.