Für die Analyse multivariater Datensätze kann die Hauptkomponentenanalyse (PCA) sehr hilfreich sein, um Muster in Datensätzen zu erkennen sowie die Dimensionen zu reduzieren. Wir geben einen Überblick, wie die PCA funktioniert, welche Befehle für eine Durchführung in R relevant sind und wie wir das Ergebnis interpretieren.
Sie möchten Hilfe bei der Analyse Ihrer multivariaten Daten? Gerne unterstützen unsere Expertinnen und Experten Sie in Form eines persönlichen Coachings oder auch mit der Datenauswertung. Kontaktieren Sie uns noch heute für eine professionelle Statistik Beratung.
Was ist eine Hauptkomponentenanalyse (PCA)?
Liegt ein multivariater Datensatz mit mehr als zwei Variablen vor, ist es schwierig, die Daten in einem Streudiagramm grafisch sinnvoll darzustellen. Bei diesem Problem können Ordinationsverfahren helfen. Eine Ordination beschreibt im Wesentlichen das Vorgehen, durch verschiedene mathematische Methoden die Dimensionen eines Datensatzes zu reduzieren. Als Ergebnis erhalten wir eine verständliche, da zweidimensionale, grafische Darstellung.
Die Hauptkomponentenanalyse (auf Englisch: principal component analysis, PCA) ist eines der ältesten Ordinationsverfahren. Die PCA wird also gebraucht, wenn multivariate Daten vorliegen, die in einem zweidimensionalen Raum interpretiert werden sollen. Alternativ kann sie auch verwendet werden, wenn für nachfolgende Analysen eine Reduktion der Dimensionen notwendig ist.
Wie funktioniert die PCA: Der mathematische Hintergrund
Die PCA sucht nach einer Möglichkeit, die Varianz im Datensatz bestmöglich, aber mit weniger Achsen abzubilden. Dafür werden neue, synthetische Achsen gefunden, entlang derer die Varianz im Datensatz möglichst hoch ist. Gleichzeitig werden dadurch die Daten dekorreliert. Die Anzahl der synthetischen Achsen entspricht der ursprünglichen Anzahl der Variablen im Datensatz. Wichtig ist, bei diesem Vorgehen die Daten selbst nicht zu verändern, sondern aus einem anderen Winkel darauf zu schauen.
Die gefundenen Achsen entsprechen dabei den Eigenvektoren der Kovarianzmatrix des Datensatzes. Um zu wissen, welcher Eigenvektor bzw. welche gefundene neue Achse am meisten der Varianz im Datensatz abbildet, können wir die zugehörigen Eigenwerte der Eigenvektoren betrachten. Je grösser diese sind, desto mehr Varianz gibt es entlang der entsprechenden Achse. Somit bildet der Eigenvektor der Kovarianzmatrix mit dem höchsten Eigenwert die erste Hauptkomponente. Die zweite Hauptkomponente ist diejenige mit dem zweithöchsten Eigenwert und repräsentiert dann dementsprechend weniger Varianz
Per Definition erfassen damit die vorderen Achsen bereits einen Grossteil der Varianz im Datensatz und die weiteren Achsen sind für die Interpretation weniger relevant. Dieses Vorgehen erreicht eine Projektion auf zwei Dimensionen, sodass mögliche Muster in den Daten leichter zu erkennen und zu interpretieren sind.
Wie berechnet man eine PCA in R?
Als Beispiel nehmen wir uns den iris-Datensatz, der standardmässig bereits in R geladen ist. Dieser enthält Informationen über die Länge und die Breite der Kron- und Kelchblätter von drei verschiedenen Schwertlilien-Arten (Iris setosa, I. versicolor, I. virginica). Will man nun nach Mustern in diesen Messwerten suchen (z.B. dass eine Art immer besonders lange Kronblätter hat) und sie dafür in einer Grafik abbilden, müsste man sich bei einem herkömmlichen Streudiagramm für zwei der vier Messwerte entscheiden. Hier kommt nun die Hauptkomponentenanalyse ins Spiel.
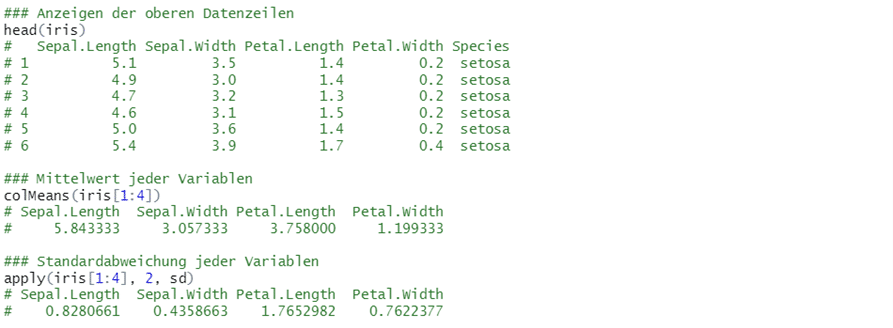
Vor der eigentlichen Analyse schauen wir uns den Datensatz einmal genauer an. Wir sehen neben den vier Messwerten auch, bei welcher Art sie jeweils gemessen wurden. Diese letzte Spalte (Species) kann man später als Referenz nutzen, für die Analyse sind aber zunächst nur die Spalten 1 bis 4 wichtig. Ausserdem kann es empfehlenswert sein, die Variablen zu standardisieren. Dies ist besonders dann wichtig, wenn die Werte in unterschiedlichen Einheiten vorliegen, damit nicht Äpfel mit Birnen verglichen werden. Dafür wird von jedem Wert der Mittelwert der entsprechenden Variable abgezogen.
Nach der Standardisierung ist der Mittelwert aller Variablen gleich Null und die Varianz entspricht Eins. Dies bietet R als Option während der Berechnung der PCA an. Alternativ kann es mit dem Befehl scale(data) durchgeführt werden. Beim Berechnen der Mittelwerte und Standardabweichungen für die Variablen aus dem Beispiel sieht man schnell, dass diese sich zwischen den Variablen jeweils unterscheiden und eine Standardisierung sinnvoll ist.
Analyse der Hauptkomponenten
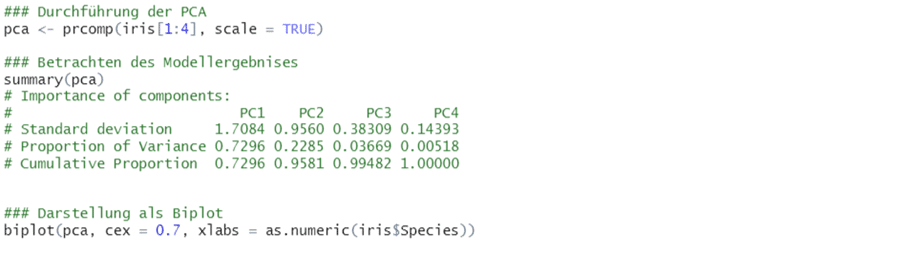
Nach der Durchführung der PCA mit dem prcomp()-Befehl (scale gibt die Option für die Standardisierung), betrachtet man die Verteilung der erklärten Varianz pro Hauptkomponente mit summary(). Die erste Achse erklärt bereits 73 % der Varianz und zusammen mit der zweiten Achse werden sogar 95,8 % der Varianz im Datensatz erklärt (vgl. „Cumulative Proportion“), was ein sehr grosser Anteil der Gesamtvarianz ist. Mit dem Befehl biplot() kann man schliesslich einen Biplot darstellen lassen, in dem die ersten beiden Hauptkomponenten gegeneinander aufgetragen werden. Um den Plot übersichtlicher zu gestalten und die Interpretation zu vereinfachen, lassen wir uns anzeigen, zu welcher der drei Arten jede Pflanze gehört.
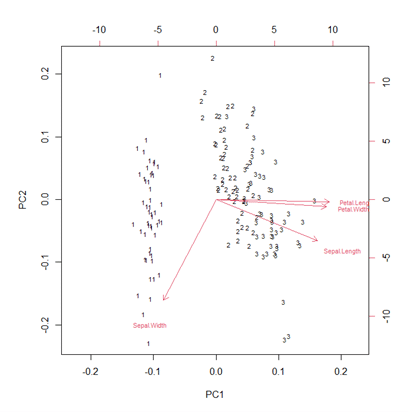
Der Biplot zeigt die Positionen der einzelnen Pflanzen im Hauptkomponentenraum und ermöglicht so die Interpretation von möglichen Zusammenhängen und Mustern. Jede Zahl repräsentiert dabei eine Pflanze. Je dichter die Zahlen beieinander platziert werden, desto ähnlicher sind sie sich gemessen an den beiden Hauptkomponenten. Hierbei ist darauf zu achten, dass einzelne Punkte nicht zu weit von den restlichen entfernt platziert sein sollten. Solche Ausreisser sollten dann genauer untersucht und möglicherweise aus der Analyse entfernt werden, damit sie das Ergebnis nicht verzerren. Neben den Individuen werden zusätzlich die Variablen in Form von Vektoren abgebildet, was Rückschlüsse auf den Einfluss der einzelnen Variablen und deren Korrelation mit den Hauptkomponenten zulässt.
Interpretation des grafischen Ergebnisses
Ein wichtiges Ergebnis einer Ordination ist eine grafische Darstellung der gefundenen Muster. Im Biplot unserer Analyse sieht man, dass die Individuen von Art 1 im Ordinationsdiagramm getrennt von den anderen beiden Arten clustert. Entlang der ersten Hauptkomponente scheint es also Unterschiede zwischen diesen beiden Clustern zu geben, während die Daten entlang der 2. Hauptkomponente innerhalb der Arten starke Variationen aufweisen.
An den Pfeilen im Diagramm kann man sehen, welche Messparameter eng mit welcher Hauptkomponente korrelieren. In unserem Diagramm verlaufen die Länge und Breite der Kronblätter (Petal.Length und Petal.Width) fast parallel zur 1. Hauptkomponente und sind somit stark mit dieser korreliert. Auch die Länge der Kelchblätter (Sepal.Length) ist noch relativ eng mit der 1. Achse korreliert, während die Breite der Kelchblätter (Sepal.Width) grösstenteils durch die 2. Hauptkomponente repräsentiert wird. Zusätzlich zu der grafischen Untersuchung ist es möglich, sich die Ladungen der einzelnen Variablen auf den Hauptkomponenten von R schriflicht ausgeben zu lassen.
Hohe Werte entsprechen dabei einer starken Korrelation mit dieser Hauptkomponente. Negative Werte bedeuten schlicht, dass eine negative Korrelation vorliegt. Auf unser Beispiel bezogen sieht man, dass die erste Hauptkomponente (PC1) hohe Ladungen in Bezug auf Sepal.Length, Petal.Length und Petal.Width aufweist, während Sepal.Width am höchsten auf die 2. Hauptkomponente (PC2) lädt. Die negative Korrelation erkennt man im Biplot daran, dass der Pfeil nach unten zeigt. Dies entspricht insgesamt auch unserem optischen Eindruck von den Korrelationen.

Zusammenfassend kann man in diesem Beispiel sagen, dass die Masse der Kronblätter ein gutes Merkmal darstellen, um Iris setosa (Art 1) von den beiden anderen Arten abzugrenzen. Diese lassen sber sich wiederum mit den vorliegenden Messdaten nicht eindeutig unterscheiden. Die Breite der Kelchblätter variiert stark innerhalb der Arten.
Dimensionsreduktion: Genauer erklärt
Ist das erklärte Ziel der PCA nicht vordergründig die Mustererkennung sondern die Dimensionsreduktion, sollte besonders auf die erklärte Varianz der Hauptkomponenten geachtet werden. In diesem Beispiel ist eine Reduktion auf zwei Dimensionen möglich, da diese zusammen einen sehr grossen Anteil der Varianz erklären. Wir betrachten noch ein anderes Beispiel, bei dem dies weniger eindeutig ist. Es handelt sich dabei wieder um einen Datensatz, der von R bereitgestellt wird. Der mtcars-Datensatz enthält Daten für 32 Fahrzeugmodelle und fasst Kraftstoffverbrauch sowie zehn weitere Merkmale zusammen. Diese liegen in verschiedenen Einheiten vor, weshalb auch hier die Durchführung einer PCA mit standardisierten Werten sinnvoll ist.
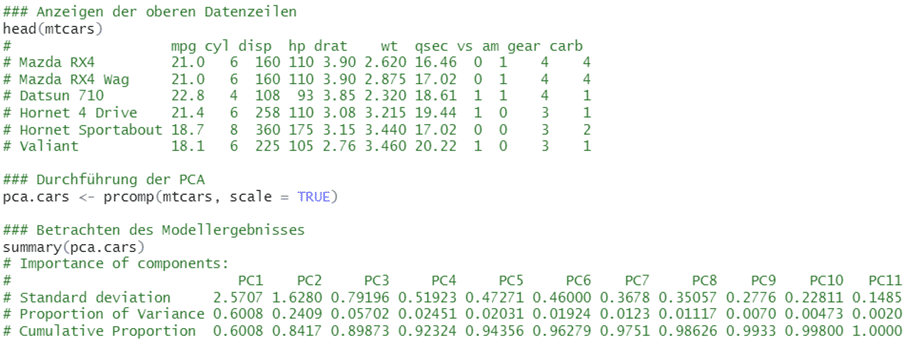
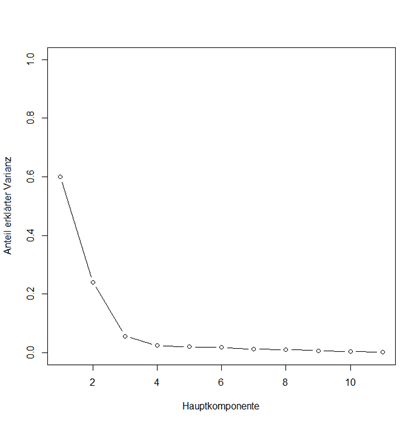
Da nun elf Variablen in die Analyse mit einfliessen, erhält man auch Ergebnisse für elf Hauptkomponenten. Um nun herauszufinden, wie viele Achsen benötigt werden, um einen Grossteil der Varianz zu erklären, haben sich sogenannte Screeplots bewährt. Im Wesentlichen ist es eine grafische Darstellung der erklärten Varianz pro Hauptkomponente (‘Proportion of Variance’ in der Summary-Tabelle). Dafür werden die Hauptkomponenten ihrer Wichtigkeit nach sortiert und der Anteil der erklärten Varianz aufgetragen. Da es hierfür in R keine implementiere Funktion gibt, ist etwas Vorarbeit nötig.

In dem Screeplot wird nun nach einem Knick gesucht, gerne auch „Ellenbogen“ genannt. Die Hauptkomponenten links von diesem sollten in weitere Analysen mit einbezogen werden. Alle weiteren tragen wenig zur Modellverbesserung bei. In unserem Fall sehen wir den Ellenbogen bei Hauptkomponente 3, was bedeutet, dass die ersten beiden Hauptkomponenten in weiteren Analysen verwendet werden sollten. Da die kumulative erklärte Varianz (siehe „Cumulative Proportion“ in der Summary-Tabelle) für diese beiden Achsen mit 84,2 % hoch ist, spricht auch dies für eine sinnvolle Reduktion auf zwei Dimensionen.
Fazit
Die Hauptkomponentenanalyse (PCA) ermöglicht die Ordination von multivariaten Daten. Im Ordinationsdiagramm können Muster und Ausreisser erkannt werden. Die ausserdem erreichte Dimensionsreduktion kann als erster Schritt für weitere Analysen verwendet werden. Neben der hier gezeigten Analyse in R lässt sich eine Faktorenanalyse in SPSS durchführen.
Bei weiteren Fragen zur Durchführung und Interpretation einer Hauptkomponentenanalyse freuen wir uns über Ihre unverbindliche Kontaktaufnahme. Gerne erstellen wir Ihnen umgehend ein unverbindliches Angebot. Nutzen Sie dazu gleich und unverbindlich unser schriftliches Kontaktformular.