Multivariate Verfahren gehören sicherlich zu den komplexesten statistischen Methoden. Dennoch sind multivariate Analysemethoden für viele Anwendungsfälle unerlässlich. So ist die multivariate Statistik von zentraler Bedeutung für die Erstellung neuer Skalen und Fragebögen. Genauso sind multivariate Verfahren extrem wichtig für die Kundensegmentierung. Aber auch für zahlreiche andere Forschungsprojekte, die Prozesse im Detail verstehen oder vorhersagen möchten, ist eine multivariate Analyse oft entscheidend.
Tatsächlich findet sich multivariate Analysemethoden in fast allen Anwendungsbereichen der Statistik. Darum wollen wir mit diesem Artikel einen ersten Überblick über multivariate Verfahren anbieten. Dabei werden wir mit Praxisbeispielen verdeutlichen, in welchen Fällen eine multivariate Statistik Sinn machen kann. Wie bereits eingangs erwähnt gehören multivariate Verfahren zu den anspruchsvollsten statistischen Methoden. Wenn Sie bei multivariater Statistik professionelle Statistik Beratung benötigen, zögern Sie also nicht einen der Experten von Novustat zu Rate zu ziehen!
Univariate versus multivariate Verfahren: Was ist der Unterschied?
Der Unterschied zwischen univariaten und multivariaten Verfahren kann durchaus etwas verwirrend sein: In verschiedenen Quellen finden sich gerne einmal unterschiedliche Definitionen. Zudem wird gerade im deutschsprachigen Raum multivariat leider oft mit multivariabel gleichgesetzt. Nach dieser Definition ist dann jedes Verfahren, welches mehr als eine Variabel betrachtet, ein multivariates Verfahren. Allerdings wäre nach dieser Definition dann auch die univariate ANOVA ein multivariates Verfahren. In einer univariaten ANOVA werden ja schliesslich mindestens 2 Variablen analysiert (abhängige & unabhängige Variablen).
Um solche Widersprüche zu vermeiden, verwenden wir für diesen Artikel die Definitionen, die weltweit am üblichsten sind:
Ein univariates Verfahren betrachtet eine einzige abhängige Variable. Ein multivariates Verfahren betrachtet zwei oder mehr abhängige Variablen gleichzeitig.
Damit gehören deskriptive Statistiken wie Mittelwert und Standardabweichung zu den univariaten Verfahren. Schliesslich wird mit diesen Werten immer nur eine einzige Variable beschrieben. Genauso zählen aber auch Verfahren wie die lineare Regressionsanalyse oder die univariate ANOVA zu den univariaten Verfahren. In diesen Verfahren wird nämlich die Auswirkung von einer oder mehreren unabhängigen Variablen auf eine abhängige Variable untersucht.
Alle multivariaten Verfahren untersuchen dagegen mindestens zwei abhängige Variablen (oder auch Zielgrössen) zur gleichen Zeit. Im Folgenden wollen wir einen groben Überblick über gängige multivariate Verfahren schaffen.
Multivariate Statistik: Explorativ oder induktiv?
Die multivariate Statistik lässt sich in die zwei Bereiche explorative Verfahren und induktive Verfahren teilen.
Explorative Verfahren dienen dazu, in den Daten vorhandene Strukturen zu entdecken. Dabei werden keine ohne nur wenige Annahmen über Zusammenhänge zwischen den Variablen gemacht.
Mit induktiven Verfahren werden dagegen Voraussagen (Hypothesen) statistisch überprüft. Induktive Verfahren können also vorherige Annahmen über Variablen testen.
Wir werden nun einige der geläufigsten multivariaten Verfahren vorstellen und anhand von Anwendungsbeispielen besprechen.
Um die unterschiedlichen Einsatzmöglichkeiten zu illustrieren, werden wir die Fluggesellschaft Hoch-Hinaus! bei verschiedenen Marktforschungsprojekten begleiten.
Explorative multivariate Methoden: Struktur der Daten entschlüsseln
Explorative Methoden kommen ohne grosse Annahmen über die Daten aus. Daher eignen sich die Methoden ideal für Situationen, in denen nicht viel Vorwissen über das Forschungsgebiet vorhanden ist. Auch für die Generierung von Hypothesen eignen sind explorative Methoden hervorragend geeignet. Diese Verfahren sind damit eng mit den Data Mining Methoden verwandt.
Die Firma Hoch-Hinaus! möchte zunächst einmal explorative Verfahren nutzen, um grundlegende Prozesse im Flugmarkt zu entdecken und zu verstehen.
Beispiele für gängige multivariate explorative Methoden sind die explorierende Faktorenanalyse (EFA) und Hauptkomponentenanalyse (PCA) sowie die Clusteranalyse.
Faktorenanalyse & Hauptkomponentenanalyse: Aus vielen Variablen werden wenige Faktoren
Die explorierende Faktorenanalyse (EFA) und Hauptkomponentenanalyse (PCA) sind verwandte Verfahren für eine multivariate Analyse. Sie dienen dazu, viele beobachtete Variablen auf einige wenige Faktoren zurück zu führen (Faktorenanalyse) oder sie zu wenigen Komponenten zusammenzufassen (Hauptkomponentenanalyse ).
In einem Fragebogen befragt das Unternehmen Hoch-Hinaus! die Teilnehmer wie Sie eine Vielzahl von Aspekten bei Fluggesellschaften bewerten. Eine Hauptkomponentenanalyse ergibt, dass sich diese vielen Faktoren in nur drei Komponenten zusammenfassen lassen: Komfort & Service, Preis und Markenprofil.
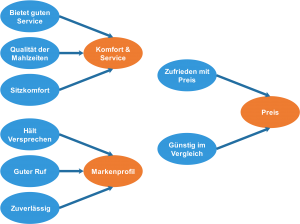
Die explorative Faktorenanalyse und Hauptkomponentenanalyse führen häufig zu ähnlichen Ergebnissen. Diese multivariate Analysemethoden unterscheiden sich aber in der Methodik und der zu Grunde liegenden Theorie. Vereinfacht gesagt, sucht die Faktorenanalyse nach den wenigen zugrunde liegenden Faktoren, die die vielen beobachteten Variablen erklären. Eine Hauptkomponentenanalyse dagegen versucht die vielen beobachteten Variablen in so wenig Komponenten wie möglich zusammenzufassen. Eine detaillierte Besprechung der Unterschiede der Verfahren finden Sie z.B. hier.
Clusteranalyse: Wie lassen sich die Daten gruppieren?
Die Clusteranalyse ist ein multivariates Verfahren, welches die Fälle in einem Datenset in verschiedene Gruppen einteilt. Dabei wird anhand von vorgegebenen Variablen bestimmt, welche Fälle sich ähneln. Diese Fälle werden dann der gleichen Gruppe zugeteilt. Häufig können Fälle in den Daten so klassifiziert werden und Muster in den Daten aufgedeckt werden. Diese Verfahren kommt besonders häufig in der Marktsegmentierung zum Einsatz.
In einer weiteren Studie möchte das Unternehmen Hoch-Hinaus! gerne die unterschiedlichen Typen an Fluggästen erforschen. Dazu werden die Studienteilnehmer befragt, wie wichtig für Sie die Aspekte Komfort & Service, Preis und Markenprofil bei der Flugbuchung sind. Auf Basis dieser Variablen wird eine Clusteranalyse vorgenommen. Dabei wird deutlich, dass die meisten Flugreisende sich in drei Segmente einteilen lassen: Preisbewusst, Geschäftsreisende und vielfliegende Urlauber.
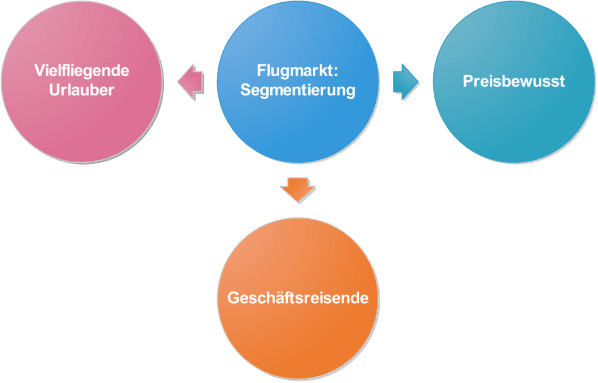
Induktive multivariate Methoden: Vorhersagen generieren und bestätigen
Induktive multivariate Statistik lässt Schlussfolgerungen auf die gesamte untersuchte Population zu. Damit sind diese Verfahren ideal geeignet, um bestehende Vermutungen zu bestätigen. Diese Verfahren eignen sich aber auch, um Modelle für Vorhersage zu entwickeln.
Durch explorative Studien hat die Fluggesellschaft Hoch-Hinaus! einige erste Erkenntnisse über den Flugmarkt gewinnen können. Diese sollen nun durch induktive multivariate Verfahren für Vorhersagen genutzt werden.
Induktive multivariate Analysemethoden, die besonders häufig verwendet werden sind z.B. die MANOVA oder die multivariate Regression.
MANOVA: Unterscheiden sich Gruppen auf mehreren Variablen?
Genauso wie die univariate Varianzanalyse (ANOVA) untersucht die multivariate Varianzanalyse (MANOVA) Unterschiede zwischen Gruppen. Allerdings werden bei der MANOVA Unterschiede auf mehreren abhängigen Variablen gleichzeitig untersucht. Eine detaillierte Erklärung hierzu gibt es in unserem Artikel über den Unterschied zwischen ANOVA SPSS und MANOVA SPSS.
Das Unternehmen Hoch-Hinaus! möchte untersuchen ob Urlaubsreisende sich von Geschäftsreisenden hinsichtlich Ihres Preisbewusstseins, ihrer Erwartung an Service & Komfort sowie in Ihrer Markenloyalität unterscheiden. Hierzu werden beide Gruppen in einer Studie befragt. Eine anschliessende MANOVA ergibt, dass die beiden Gruppen sich über alle abhängigen Variablen unterscheiden. Folgeuntersuchungen ergeben, dass Urlaubsreisende preisbewusster sind. Dafür sind Sie aber auch weniger anspruchsvoll was den Service und Komfort angeht.
Multivariate Regression: Vorhersagen für mehrere Zielvariablen
Eine multivariate Regression erlaubt das modellieren von linearen Zusammenhängen zwischen Variablen. Damit ähnelt die multivariate Regression der klassischen univariaten linearen Regression. Nur hat eine multivariate Regression statt einer abhängigen Variablen gleich mehrere Zielvariablen auf einmal. Somit lassen sich Zusammenhänge für mehrere Zielvariablen kombiniert überprüfen. Für dieses Verfahren wird das so genannte allgemeine lineare Modell oder generalisierte lineare Modell (GLM) eingesetzt. Hierbei handelt es sich um eine Weiterentwicklung der linearen Regression. Es ist universeller einsetzbar; dieses Verfahren kann also mehr Anwendungsfälle abdecken.
Das Unternehmen Hoch-Hinaus! vermutet, dass der Wert der gekauften Flüge (letzte 12 Monate), der Wert der gekauften Extraleistungen (letzte 12 Monate) sowie die Markenloyalität von dem Zusammenspiel verschiedener Faktoren zusammenhängt. Es soll untersucht werden, ob der Unterschied zwischen Urlauber und Geschäftsreisenden durch Preisbewusstsein beeinflusst wird. Umfragedaten von Urlaubs- und Geschäftsreisenden werden hierzu mithilfe einer multivariaten Regression (GLM) ausgewertet. Die multivariate Statistik ergibt, dass nur preisbewusste Urlaubsreisende sich von Geschäftsreisenden über alle abhängigen Variablen hinweg unterscheiden. Weitere Analysen ergeben, dass preisbewusste Urlaubsreisende weniger loyal sind und insgesamt wenig Geld für Flüge und Extraleistungen ausgeben.
Multivariate Verfahren: Unersetzliche Tools für komplexe Zusammenhänge
Wann immer Sie besonders komplexe Zusammenhänge analysieren möchten, bieten sich multivariate Verfahren an. Multivariate Statistik ist extrem vielseitig und flexibel, aber eben auch sehr anspruchsvoll. Dieser Artikel hat einen ersten Überblick über die möglichen Einsatzmöglichkeiten der multivariaten Statistik gegeben. Allerdings sind multivariate Verfahren enorm vielfältig und so kann dieser Artikel nur eine kleine Auswahl an möglichen Analysemethoden darstellen. Für eine umfassende Statistik Beratung zu dem richtigen Verfahren können sie sich jederzeit an die Experten von Novustat wenden!
