ANOVA und MANOVA sind zwei der nützlichsten statistischen Verfahren, um Unterschiede zwischen Gruppen festzustellen. Dabei ist für ANOVA SPSS ein beliebtes Tool zur Durchführung. Aber es ist auch möglich für MANOVA SPSS verwenden. Dabei bezeichnen die Abkürzungen ANOVA und MANOVA zwei unterschiedliche Arten der Varianzanalyse. Aber was ist eigentlich der Unterschied zwischen ANOVA und MANOVA? Und wann benötigt man welches Verfahren?
Diese und andere Fragen möchten wir in diesem Artikel auflösen. Dabei werden wir eine grundlegende Einführung zum Thema ANOVA und MANOVA in SPSS anbieten. Ausserdem lernen Sie, wann Sie welches Verfahren wählen sollten. Wenn Sie weitere Fragen zur SPSS Auswertung oder anderen statistischen Themen haben kontaktieren Sie am Besten unsere Experte für eine Statistik Beratung.
Dieser Artikel beantwortet folgende Fragen
- Was ist der Unterschied zwischen ANOVA SPSS vs. MANOVA SPSS?
- Wann sollte ich eine ANOVA einsetzen? Wann sollte ich eine MANOVA einsetzen?
- Wie führe ich eine ANOVA durch? Wie führe ich eine MANOVA durch?
ANOVA SPSS / MANOVA SPSS: Zwei Varianten der Varianzanalyse
Wie eingangs erwähnt stellen ANOVA und MANOVA beide eine Spielart der Varianzanalyse da. Dabei steht ANOVA für Analysis of Variance oder zu deutsch einfach Varianzanalyse. ANOVA bezeichnet also eine einfache Varianzanalyse. MANOVA steht für Multivariate Analysis of Variance, oder eben multivariate Varianzanalyse. Dabei stellt eine MANOVA gewissermassen eine Weiterentwicklung der ANOVA dar. Eine MANOVA kommt daher oft zum Einsatz, wenn eine einfache ANOVA nicht mehr ausreicht.
Um den Unterschied genauer zu erklären gehen wir deshalb erst einmal auf die einfaktorielle Varianzanalyse ein (ANOVA SPSS). Danach erklären wir den Unterschied zu MANOVA und in welchen Fällen eine MANOVA gegenüber der ANOVA Sinn macht. Die folgende Tabelle gibt aber schon einmal einen ersten Überblick über beide Verfahren:
| ANOVA | MANOVA | |
| Nullhypothese | \(H_{0}:\mu_{1}=\mu_{2}…=\mu_{k}\) | \(H_{0}:\begin{pmatrix} \mu_{11}\\ \mu_{21}\\ …\\ \mu_{p1} \end{pmatrix} = \begin{pmatrix} \mu_{12}\\ \mu_{22}\\ …\\ \mu_{p2} \end{pmatrix} = \begin{pmatrix} \mu_{1k}\\ \mu_{2k}\\ …\\ \mu_{pk} \end{pmatrix} \) |
| Abhängige Variable | 1 kontinuierliche Variable | 2+ kontinuierliche Variablen |
| Unabhängige Variable | 1+ kategoriale Variable(n) | 1+ kategoriale Variable(n) |
ANOVA SPSS: Unterscheiden sich Gruppen auf einem Faktor?
Eine ANOVA ist immer dann sinnvoll, wenn man Unterschiede für eine Variable zwischen verschiedenen Gruppen feststellen will.
Nehmen wir einmal folgendes Beispiel: Die Firma Gaga Cola hat einen Geschmackstest für 5 Geschmacksrichtungen ihres Softdrinks durchgeführt. Gaga Cola möchte nun testen, ob es Unterschiede in der Bewertung dieser 5 Geschmacksrichtungen gibt. In so einem Fall wäre eine ANOVA ein sinnvolles statistisches Verfahren. Für unser Beispiel gehen wir davon aus, dass bereits eine Annahmenprüfung für ANOVA durchgeführt wurde.
Dabei stellt die Variable, für die wir auf Unterschiede testen (Bewertung) die abhängige Variable dar. Die gruppierende Variable (Geschmacksrichtungen) wäre dann eine unabhängige Variable.
Eine Frage der Varianz
Um Unterschiede bei der abhängigen Variablen (z.B. Kundenzahlen) festzustellen, wird bei der ANOVA die Varianz dieser Variable untersucht. Dabei ist die Varianz einfach ein statistisches Mass dafür, wie sehr die Variable zwischen den unterschiedlichen Messungen schwankt. Die Varianz wird innerhalb der Varianzanalyse auch als mittleres Abweichungsquadrat bezeichnet (Abkürzung MQ).
Solche Schwankungen können durch eine Vielzahl von Gründen entstehen. Mögliche Ursachen von Varianz wären etwa Messfehler (Bewertung falsch aufgeschrieben), Laune des Testers, generelle Tendenz des Testers (gibt z.B. eher niedrige Bewertungen ab), und viele weitere zufällige Faktoren. Eine mögliche Ursache für Unterschiede zwischen den Messwerten wäre aber eben auch die jeweilige Geschmacksrichtung. Die gesamte Varianz setzt sich also zusammen aus zufälligen Schwankungen und Schwankungen aufgrund der Gruppenzugehörigkeit (Geschmacksrichtung):
\( MQT = MQA+MQE\)Dabei steht MQT für die „totale Varianz“ (Varianz insgesamt). MQA steht für die Varianz erzeugt durch „Faktor A“ (hier Geschmacksrichtung). MQE steht für die verbleibende zufällige Varianz oder auch die Varianz, die als störender „Messfehler“ anzusehen ist (E steht für „Error“).
Uns interessiert nun ob die Geschmacksrichtung Unterschiede erzeugt, die gegenüber der restlichen zufälligen Varianz statistisch signifikant ist.
Dafür wird die Varianz durch die Geschmacksrichtung verglichen mit der zufälligen Varianz. Das Verhältnis der beiden Varianzen kann dann mit der F-Verteilung auf Signifikanz geprüft werden.
\( F = \frac{MQA}{MQE}\)Anders gesagt: Wir sprechen von einem signifikanten Effekt, wenn der Einfluss von Geschmacksrichtung auf die Bewertung gegenüber der üblichen zufälligen Schwankung auffällig gross ist. Wie gross „auffällig gross“ für einen signifikanten Effekt ist hängt dabei wie immer von der Stichprobengrösse ab. Allerdings sagt ein signifikanter Effekt noch nichts darüber aus, welche der Gruppen sich unterscheiden. Dafür sind so genannten Post-Hoc Tests nötig
Eine detaillierte Beschreibung des mathematischen Verfahrens hinter der einfaktoriellen Varianzanalyse finden Sie z.B. hier. Glücklicherweise können wir uns die notwendigen mathematischen Berechnungen auch von SPSS abnehmen lassen.
So verwenden Sie für die ANOVA SPSS
In SPSS finden Sie das Menü für die Varianzanalyse unter Analysieren Allgemeines Lineares Modell Univariat. Im Menü für die ANOVA SPSS Analyse wählen Sie dann zuerst die entsprechende abhängige Variable aus. Kategoriale Abhängige Variablen fügen Sie dem Abschnitt „Feste Faktoren“ hinzu.
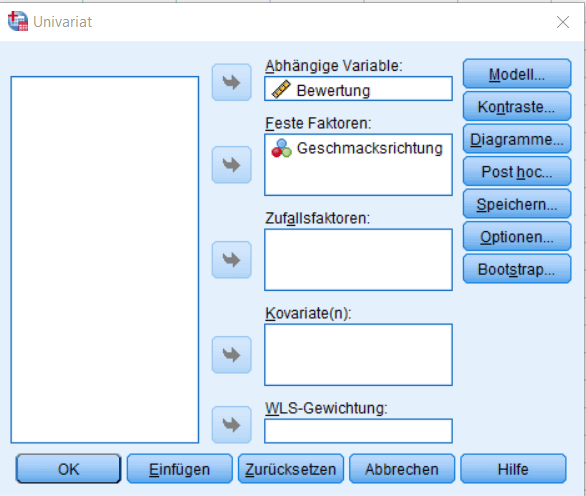
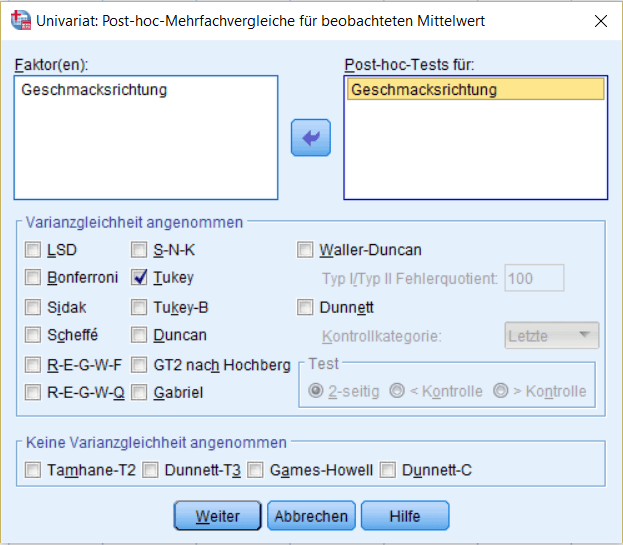
Für unser Anwendungsbeispiel fordern wir unter „Post hoc…“ noch eine post hoc Analyse mit Tukeys Korrektur für multiples Testen an.
Nachdem die Analyse bestätigt wird, zeigt SPSS die Ausgabe für die ANOVA.
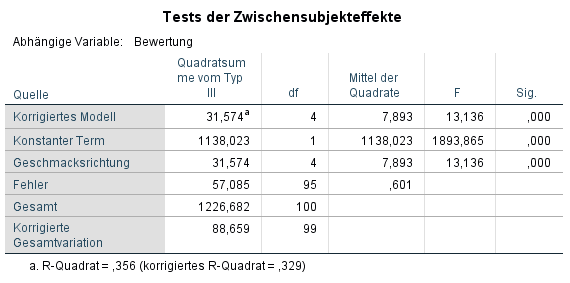
In diesem Fall war der F-Test für Geschmacksrichtung signifikant, F (4, 95) = 13,14, p > 0,001. Es gab also signifikante Unterschiede zwischen den Geschmacksrichtungen hinsichtlich der Bewertung. Welche Geschmacksrichtungen sich nun genau unterscheiden können wir im nächsten Schritt ermitteln.
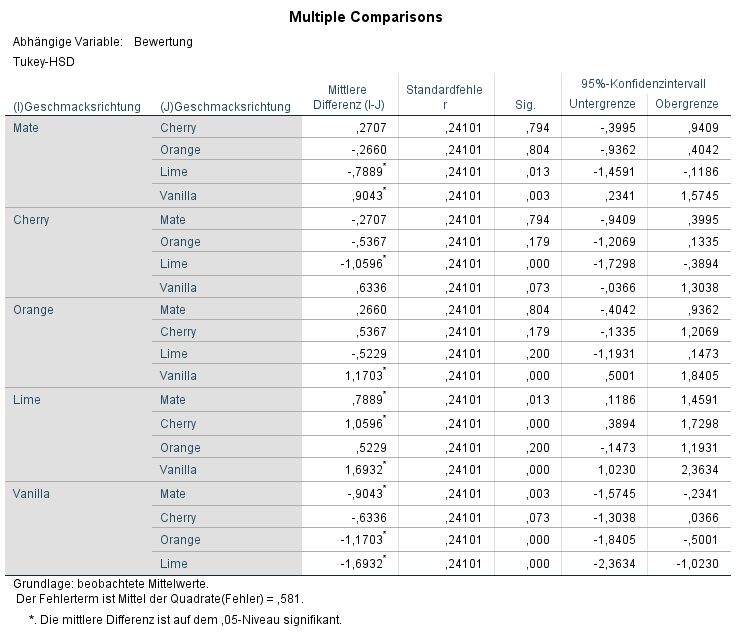
Für dieses Beispiel fallen die post hoc Analyse eindeutig aus: Lime war signifikant beliebter als alle anderen Sorten, Diffs > 0,52, ps < 0,02. Vanilla war dagegen unbeliebter als Mate, Orange und Lime, Diffs < -0,90, ps < 0,001.
MANOVA SPSS: Aus einer abhängigen Variablen werden viele
In manchen Studien wird nicht nur eine abhängige Variable erhoben, sondern gleich mehrere parallel.
Dazu ein weiteres Beispiel: Gaga Cola hat sich entschlossen die Geschmacksrichtung Lime auf den Markt zu bringen. Für diesen neuen Softdrinks hat Gaga Cola nun drei Verpackungen entworfen. In einer weiteren Studie wurden Versuchsteilnehmern die Verpackungen vorgeführt und ein Geschmackstest wurde durchgeführt. Daraufhin haben die Teilnehmer wieder den Geschmack des Getränks bewertet. Ausserdem wurden Sie aber auch zu ihrer Wahrnehmung der Marke und nach ihrer Kaufintention befragt. Wir verfügen nun also über drei abhängige Variablen (Geschmack, Markenwahrnehmung und Kaufintention).
Eine Möglichkeit wäre natürlich einfach eine einfaktorielle Varianzanalyse per abhängiger Variable durchzuführen. Dabei würden wir durch multiples Testen aber die Chance auf einen Fehler 1. Art erhöhen. Ausserdem treten manche Unterschiede zwischen den Verpackungen erst zu Tage, wenn alle abhängigen Variablen kombiniert betrachtet werden. In diesem Fall bietet es sich daher an für eine MANOVA SPSS zu verwenden.
Eine MANOVA ist eine Varianzanalyse mit mehreren abhängigen Variablen (multivariate Varianzanalyse). Dabei wird untersucht ob es einen multivariaten Unterschied zwischen den Gruppen über alle abhängigen Variablen hinweg gibt.
So verwenden Sie für eine MANOVA SPSS
Für das folgende Beispiel gehen wir davon aus, dass eine Annahmeprüfung für eine MANOVA durchgeführt wurde. Das Menü für MANOVA finden Sie unter Analysieren –> Allgemeines Lineares Modell –> Multivariat.
Das Menü für eine MANOVA gestaltet sich dabei ähnlich wie bei einer ANOVA. Der wesentliche Unterschied besteht darin, dass man mehrere Faktoren als abhängige Variablen bestimmen kann.
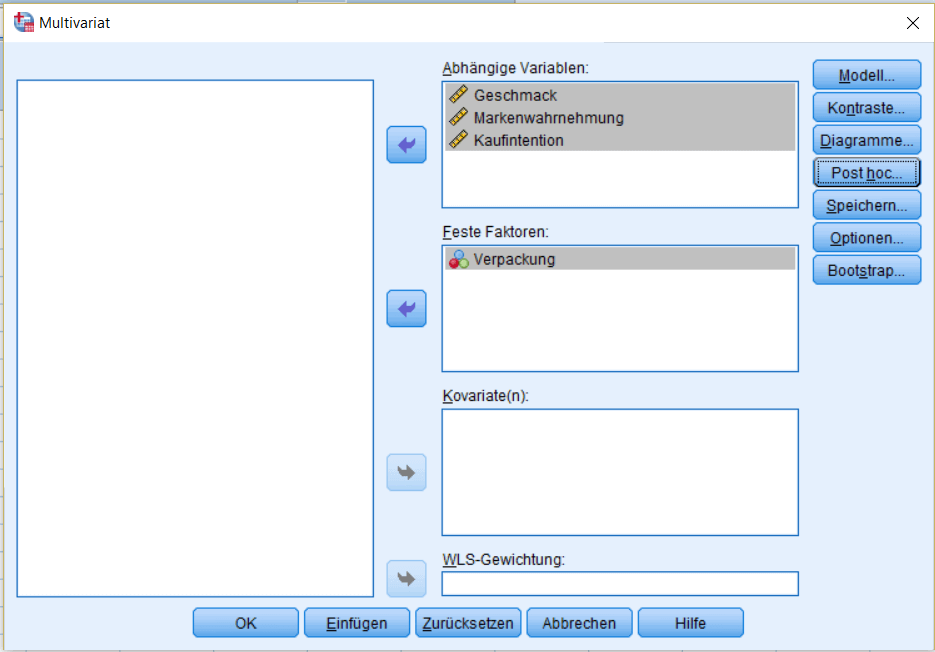
Betrachtet man für die MANOVA SPSS Ausgabe, so sieht man zunächst die Ergebnisse für multivariate Unterschiede zwischen den Gruppen.
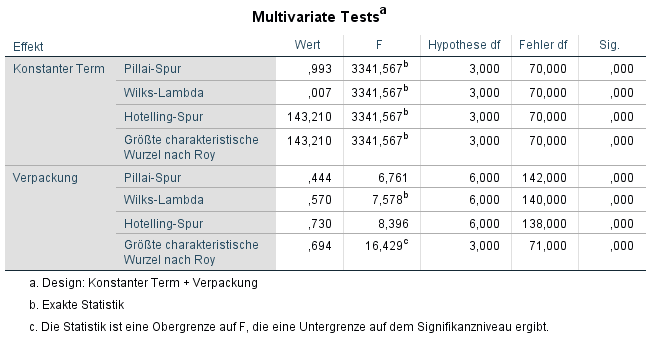
SPSS listet in der Ausgabe mehrere multivariate Tests auf. Genauso werden annähernde F-Werte für jeden Test aufgelistet. Der üblichste Test für die multivariate Varianzanalyse ist jedoch Wilks Lambda. Es ist deutlich zu sehen, dass Verpackung einen signifikanten multivariaten Einfluss über alle Variablen hinweg hatte, Wilks λ = 0,57, F(6, 140) = 7,58, p < 0,001.
Bei einem signifikanten multivariaten Effekt werden dann ANOVAs für jede abhängige Variable durchgeführt. Dies lässt sich in der MANOVA SPSS Ausgabe anhand der nächsten Tabelle schnell erledigen.
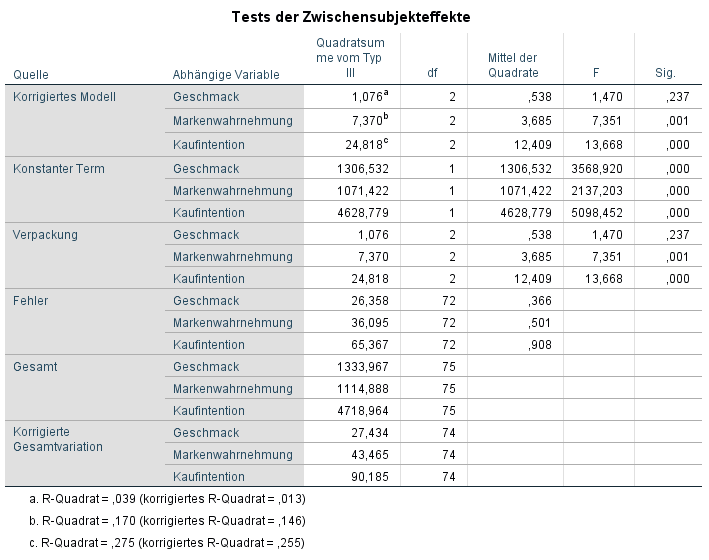
In diesem Beispiel hatte Verpackung einen signifikanten Einfluss auf die Markenwahrnehmung, F(2, 74) = 7,35, p = 0,001 und die Kaufintention, F(2, 74) = 13,67, p < 0,001. Die Bewertung des Geschmacks wurde hingegen nicht durch die Verpackung beeinflusst, F(2, 74) = 1,47, p = 0,24.
Im nächsten Schritt kann durch eine post hoc Analyse bestimmt werden, welche der Verpackungen sich hinsichtlich Markenwahrnehmung und Kaufintention von den anderen unterscheiden. Für post hoc Tests kann man genauso vorgehen wie bei einer einfachen ANOVA.
ANOVA SPSS versus MANOVA SPSS: Zusammenfassung
In diesem Artikel haben wir einen groben Überblick über die Verfahren ANOVA und MANOVA in SPSS gegeben. Wir haben dargestellt wann Sie welches Verfahren benötigen und wie Sie das jeweilige Verfahren in SPSS durchführen. Selbstverständlich kann dieser Artikel nur eine erste Orientierungshilfe zu diesem komplexen Thema geben. Für weitere Unterstützung können Sie aber jederzeit unsere Statistik Hilfe anfordern.
