Die lineare Regression ist eines der vielseitigsten statistischen Verfahren: So ist die lineare Regression ein nützliches Verfahren für Prognosen (z.B. Vorhersage von Besucherzahlen). Aber für die Untersuchung von Zusammenhängen (z.B. Einfluss von Werbeausgaben auf die Verkaufsmenge) ist die Verwendung einer linearen Regression oft sinnvoll. In diesem Artikel möchten wir daher das Thema lineare Regression näher beleuchten. Dieser Artikel beschäftigt sich dabei hauptsächlich mit dem Thema einfache lineare Regression: Wie können Beziehungen zweier Variablen beschrieben und modelliert werden? Einfache lineare Regression ist dabei in zweierlei Hinsicht zu verstehen: Als einfache lineare Regression wird eine lineare Regressionsanalyse bezeichnet, bei der nur ein Prädiktor berücksichtigt wird. In diesem Artikel soll darüber hinaus auch die Einfachheit im Sinne von einfach und verständlich erklärt als Leitmotiv dienen. Also keine Angst vor komplizierten Formeln!
Wenn Sie Unterstützung bei der Durchführung oder Interpretation einer Regression benötigen, helfen unsere Statistiker Ihnen gerne weiter. Kontaktieren Sie uns für eine kostenlose Beratung & ein unverbindliches Angebot.
Lineare Regression einfach erklärt mit Praxisbeispiel
Stellen Sie sich folgende Situation vor: Die Firma Kuschelwuschel hat in jahrelanger Entwicklung ein neues Haarwuchsmittel entwickelt. Dieses Mittel soll nun in einer klinischen Studie an 10 gesunden Probanden erprobt werden. Darauf möchte man anhand der gewonnenen Daten das Wachstum unter dem Shampoo quantifizieren und das Haarwachstum vorhersagen.
Zuerst stellen wir mit einem Streudiagrammen (Streudiagramm) die Zusammenhänge grafisch dar. Über ein Model werden dann Schätzer für die Effekte sowie die Tests auf Effekte berechnet. Die lineare Regression wird dabei exemplarisch mit dem Programm SPSS der Firma IBM durchgeführt und interpretiert.
Wir beschreiben in diesem Blog die einfache lineare Regression – einfach erklärt. Damit werden wir auch schon alle Hände voll zu tun haben. Nähere Informationen zu anderen Modellierungen finden Sie in unserem Glossar.
Sie benötigen Hilfe bei der Durchführung einer linearen Regression? Wünschen Sie ein individuelles Coaching zum Verständnis und Anwendung der linearen Regression? Möchten Sie die lineare Regression nutzen, um die Auswertung eines Fragebogen tiefgehend und professionell durchzuführen?
Von der Statistik Nachhilfe bis hin zur Unterstützung durch eine vollständige statistische Auswertung: Unsere Experten helfen Ihnen schnell und kompetent weiter!
Diese Fragen beantwortet dieser Artikel:
- Wozu benötigt man eine lineare Regression?
- Was sind kleinste Quadrate (KQ)?
- Was versteht man unter einem Streudiagramm (engl. Streudiagramm)?
- Wie gut beschreibt meine Regressionsgerade die Daten?
- Wie erkenne ich, ob eine Einflussvariable signifikant ist?
- Was muss man bei der linearen Regression beachten? Welche Voraussetzungen müssen erfüllt sein?
- Was versteht man unter dem Begriff „multiple lineare Regression“?
Eine haarige Angelegenheit und eine lineare Regression
Unsere Kopfhaare wachsen im Jahr 13 cm.
Könnten wir diese Aussage so stehen lassen, dann wäre die Forschungshypothese der Firma Kuschelwuschel schon weitestgehend beantwortet. Eine solch deterministische Aussage mit exakten Zusammenhängen entspricht allerdings nicht der Realität: Denn die Kopfhaare eines Menschen wachsen in einem festen Zeitraum unterschiedlich stark. Dies ist z.B. abhängig von Jahreszeit, Geschlecht, Haarpflege, Witterungseinflüssen, Alter, genetischer Disposition,… Darüber hinaus mischt sich oft noch eine grosse Portion Zufall in Form von unkalkulierbaren Messfehlern oder Störgrössen dazu.
Der erste Schritt besteht darin, zuerst die Zusammenhänge zwischen den Variablen kennen zu lernen und zu beschreiben.
Betrachten wir hierzu die Messwerte der Haarlängen von 10 Studenten. Diese wurden in der Studie von Kuschelwuschel mit einem innovativen Shampoo behandelt:
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| X: Haarlänge in cm Beginn | 15 | 3 | 8 | 12 | 56 | 35 | 13 | 57 | 25 | 29 |
| Y: Haarlänge in cm nach 10 Wochen (70 Tage) Behandlung | 16 | 4 | 15 | 15 | 58 | 40 | 22 | 65 | 19 | 30 |
Zur Vereinfachung der Schreibweise werden die Messwerte zu Studienbeginn mit X bezeichnet, die Haarlängen nach 70 Tagen als Y.
Allgemein nennt man X Einflussvariable, unabhängige Variable oder Prädiktor.
Y wird dahingegen als abhängige Variable, Zielvariable oder auch Response bezeichnet.
Die Messwerte (X; Y) kann man in einem sogenannten Streudiagramm (engl. Scatterplot) veranschaulichen. Auf der x-Achse wird dabei die Einflussvariable abgetragen, die Zielvariable auf der Ordinate.
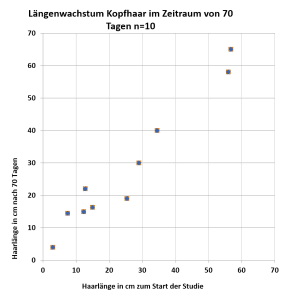
Im Diagramm ist ein positiver linearer Zusammenhang erkennbar. Der Pearson Korrelationskoeffizient ergibt sich dementsprechend als r = 0,973.
Nach welchen Kriterien legt man eine optimale Gerade durch die Punktewolke?
Eine Gerade durch die Punktewolke ist gegeben durch die Formel \(Y=a+b \cdot X\). Dabei bezeichnet a den y-Achsenabschnitt und b die Steigung der Regressionsgeraden. In der Regression heisst a auch Intercept und b Regressionskoeffizient oder slope.
- Dabei soll die Regressionsgerade durch den Mittelwert der X-Werte ( \(\bar{X}\)) und den Mittelwert der Y-Werte ( \(\bar{Y}\)) gelegt werden. Zunächst wird also das arithmetische Mittel der X-Werte und der Y-Werte berechnet
\(\bar{X}=\frac{1}{n}\cdot\sum_{i=1}^{n}x_i\)
\(=\frac{1}{10} \cdot\left(15+3+7,5+12,5+56+34,5+12,8+56,8+25,4+29\right)=25,23\)
\(\bar{Y}=\frac{1}{n} \cdot \sum_{i=1}^{n}y_i\)
\(=\frac{1}{10} \cdot \left( 16,3+4+14,5+15+58+40+22+65+19+30\right) = 28,38\)
2. Nun wird die Gerade so durch den Punkt \(\left(\bar{X},\bar{Y}\right) \) gelegt, dass die Abweichung der beobachteten Y-Werte zu den Y-Werten der Regressionsgerade insgesamt minimiert wird. Die Differenz der beobachteten y-Werte von den vorhergesagten y-Werten der Regressionsgeraden nennt man dabei Residuen. Residuen können positive oder negative Werte haben, je nachdem ob die Datenpunkte über- oder unterhalb des Mittelwertes liegen. Sehr hohe oder sehr niedrige Residuen sind ein Indiz für eine „ungünstige“ Gerade. Damit extreme Residuen ein hohes Gewicht bekommen, werden die einzelnen Residuen quadriert. Die optimale Regressionsgerade ist die Gerade, bei der die Summe der quadrierten Residuen so klein wie möglich ist.
Dieses Verfahren wird auch Methode der Kleinsten Quadrate (engl. OLS Method: Ordinary least squares method) genannt. Die Quadrate lassen sich auch im Streudiagramm veranschaulichen:

Jede andere Gerade hat eine „grössere“ quadrierte Residuensumme.
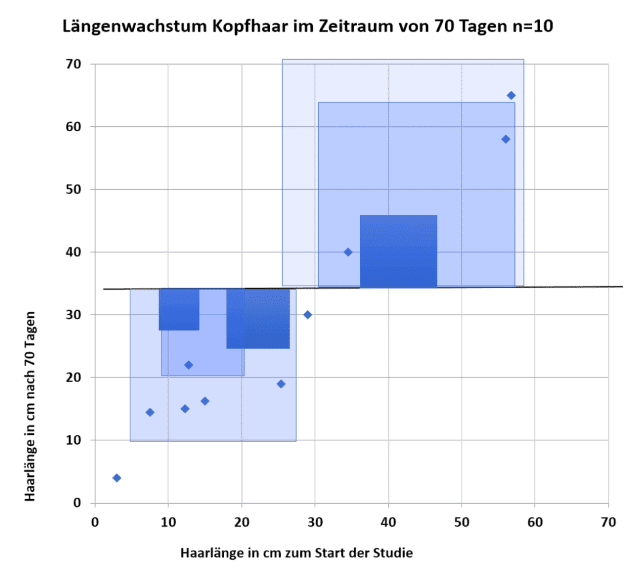
Mit dieser Forderung ist die Regressionsgerade eindeutig definiert und der Intercept a und der Regressionskoeffizient b lassen sich berechnen.
Die Formeln für die Berechnung sind in den Lehrbüchern für Statistik zu finden. Im Folgenden werden wir die Berechnung mit statistischer Software beschreiben.
Haargenau: Lineare Regression einfach erklärt mit SPSS
Zunächst gibt man die 10 Messwerte in die Dateneingabe von SPSS ein. Eine Einführung zu dem Programm ist in unserem Glossar-Artikel zu SPSS zu finden. Anschliessend wählt man im Menüpunkt Analysieren – Regression – Linear. Als abhängige Variable übergibt man die Messwerte am Studienende. Als unabhängige Variable wird die Haarlängen zu Beginn der Studie ausgewählt.
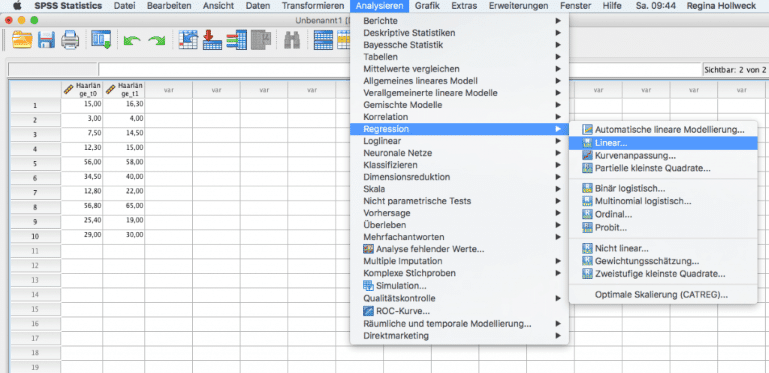
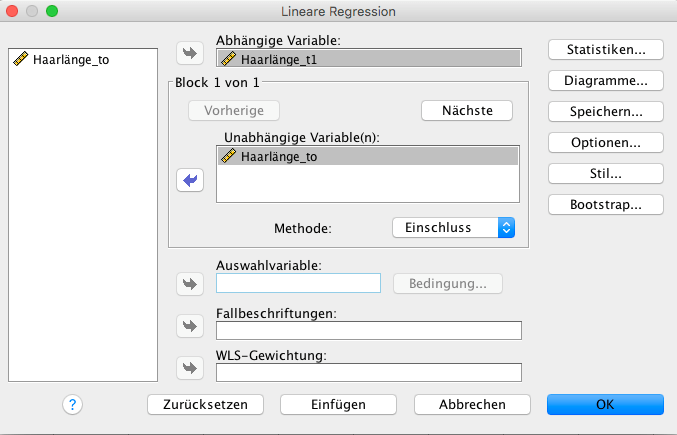
So interpretiert man eine lineare Regression mit SPSS
Bestätigt man die Angaben, erhält man im Ausgabefenster folgende Berechnungen:
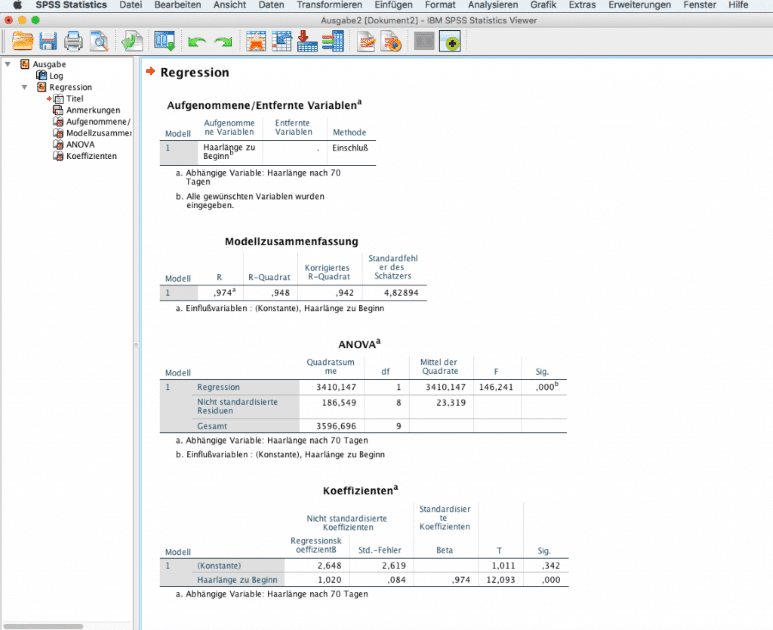
Im Ausgabefenster erscheinen 4 Tabellen:
- Aufgenommenen/Entfernte Variablen: Hier wird zusammengefasst, welche abhängigen und unabhängigen Variablen in das Modell eingeschlossen werden.
- Modellzusammenfassung: In dieser Tabelle werden Masszahlen für die Modellgüte angegeben. R gibt den Pearson Korrelationskoeffizienten an, R-Quadrat den quadrierten Wert. R2 wird auch als Bestimmtheitsmass bezeichnet. Das Bestimmtheitsmass gibt an, wie viel der Variabilität der Daten das Modell erklärt wird. Falls R2 den Wert 1 annimmt, liegen alle Punkte exakt auf der Gerade. Je näher der Wert sich 1 annähert, umso „enger“ liegen die Daten um die Gerade. R2 erhöht sich automatisch bei Hinzunahme mehrerer Variablen, ohne dass ein wirklicher Informationsgewinn damit verbunden ist. Aus diesem Grund gibt SPSS ein korrigiertes R2 aus, welches unabhängig von der Anzahl der Einflussvariablen ist. In unserem Beispiel mit nur einer Einflussvariable spielt dies keine Rolle.
- ANOVA: Bei der Varianzanalyse prüft zunächst ein F-Test, ob das gesamte Modell signifikant ist. Damit kann man entscheiden, ob sich die Vorhersage der Zielvariable durch die unabhängigen Variablen im Modell verbessert. Dazu wird der Gesamtvarianz der Daten aufgeteilt in zwei Teile. Den ersten Teil bildet der Beitrag, der durch das Modell erklärt wird. Den zweiten Teil bildet dahingegen eine unerklärte, zufällige Komponente. Das Modell ist umso besser, je mehr Variabilität der Daten durch die Regression erklärt werden kann.
In dem Beispiel ist das Model signifikant mit einem p-Wert <0,001.
- Koeffizienten: In dieser Tabelle sind die Schätzer für die Regressionsgerade zu finden. Mit Konstante wird der Intercept (a) bezeichnet. Somit ergibt sich im Beispiel folgende Regressionsgerade:
\(Y=2,648+1,020 \cdot X\)
Regressionskoeffizienten sinnvoll interpretieren
Der Intercept gibt die Konstante an, mit der die Haare innerhalb der 70 Tage wachsen. Der Regressionskoeffizient b=1,020 zeigt, wie sich die Haarlänge in Abhängigkeit von der Ausgangslänge verhält. Der Faktor ist positiv, daran erkennt man, dass Personen mit einem langen Ausgangshaar höheres Wachstum im Beobachtungszeitraum zeigen. Wenn die Haarlänge um eine Einheit (cm) steigt, so erhöht sich die Endlänge um den Faktor 1,020. Diesen Effekt sieht man gut, wenn man die Formel für die Vorhersage verwendet: Susis Haare haben eine Länge von 50 cm. In 70 Tagen haben sie eine geschätzte Länge von \(2,648+1,020\cdot 50cm=53,648 cm\). Die Haare von Susis Freundin sind 10 cm länger, nach 70 Tagen werden die Haare um \(10\cdot 1,020\) länger geschätzt als die von Susi, wären daher 63,848 cm lang.
Der Standardfehler ist eine Masszahl für die Streuung der Regressionsparameter. Die Spalte standardisierte Parameter ist im univariaten Regressionsmodell mit einer Einflussvariable nicht relevant. Die letzten beiden Spalten der Tabelle beinhalten die Ergebnisse des statistischen Tests. Dabei wird die Nullhypothese mittels eines T-Tests geprüft, ob der Parameter gleich Null und damit unbedeutend ist. Signifikante p-Werte zeigen, dass die Variable einen nachweisbaren Effekt auf die Zielgrösse hat. Im Gegensatz zu ANOVA wird hierzu jeder Koeffizient einzeln untersucht.
Haarspaltereien: Voraussetzungen für lineare Regression einfach erklärt
Zunächst muss der Zusammenhang der Zielvariable und der Einflussvariable linear sein. Gegebenenfalls können Transformationen angewendet werden, um dies zu gewährleisten. Ein Mass für die Linearität zweier Variablen ist dabei der Pearson Korrelationskoeffizient. Im Streudiagramm kann man diesen Zusammenhang untersuchen.
Darüber hinaus müssen die folgenden drei Bedingungen hinsichtlich der Residuen erfüllt sein:
1. Die Residuen sind voneinander unabhängig
Diese Voraussetzung ist meist dadurch erfüllt, dass eine echte Zufallsstichprobe vorliegt, in der alle Beobachtungen voneinander unabhängig sind. Im Zweifelsfall kann auch der Durbin Watson Test herangezogen werden. Im Falle eines signifikanten p-Wertes muss von einer Autokorrelation der Residuen ausgegangen werden. P-Werte >0,05 beweisen allerdings nicht die Unabhängigkeit der Residuen.
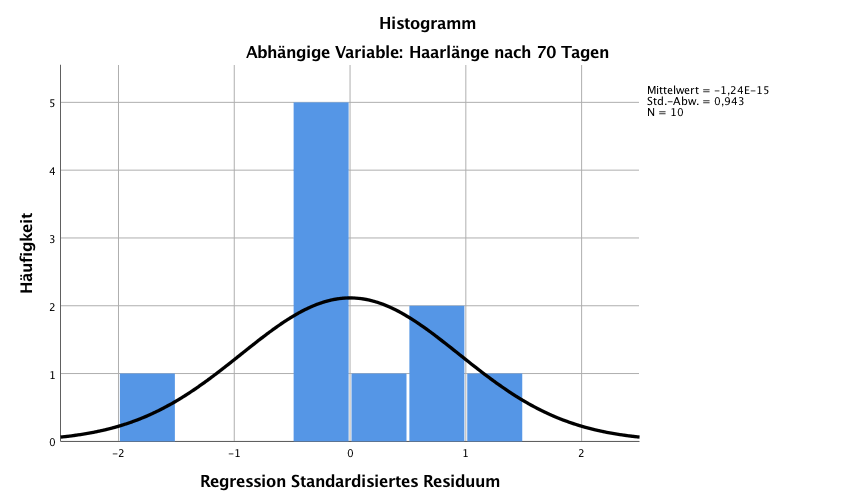
2. Die Residuen sind annähernd normalverteilt
Dies kann man am besten in einem Histogramm der Residuen grafisch überprüfen. Das Histogramm sollte dabei symmetrisch um eine Mitte sein und bei grösseren Fallzahlen sich an eine Normalverteilung annähern. Bei kleineren Fallzahlen kann man keine perfekte Übereinstimmung erwarten. Auch die Überprüfung der Normalverteilung kann mittels eines Tests vorgenommen werden. Aufgrund der Natur des statistischen Testens kann aber mit dem Kolmogorov Smirnov Test nur eine Abweichung von der Normalverteilung nachgewiesen werden.
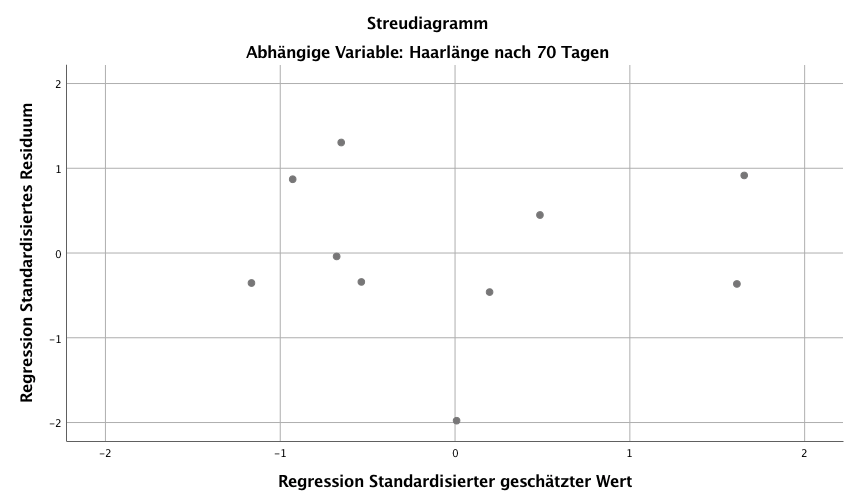
3. Die Streuung der Residuen ist konstant im gesamten Wertebereich von Y (Homoskedastizität)
Trägt man in einem Streudiagramm (Streudiagramm) die Residuen gegen die vorhergesagten Werte auf, so sollten sich keine Muster zeigen. Bei Vorliegen von Homoskedastizität liegen die Punkte daher gleichmässig verteilt im gesamten Wertebereich von Y.
Haarwachstum im n-dimensionalen Raum: Die multiple lineare Regression
Die gleichen Ideen kann man nutzen, um eine Zielvariable durch viele Einflussvariablen zu beschreiben. In diesem Fall spricht man dann von einer multiplen linearen Regression. Das zugehörige Regressionsmodell hat dabei die Form:
\(Y=a+b_1\cdot X_1+b_2\cdot X_2+\ldots + b_n \cdot X_n\).
Andere Einflussgrössen könnten beispielsweise Geschlecht oder Alter sein. Alle obigen Annahmen des univariaten Modells gelten dabei analog. Mit Matrixalgebra und einem Computer können solch komplexe Problemstellungen effizient bearbeitet werden. Die Berechnungen finden im n-dimensionalen Raum statt. In der grafischen Darstellung ist man allerdings auf das 2-dimensionale Blatt beschränkt. Die grafischen Beziehungen müssen deshalb paarweise untersucht werden.
Zusammenfassung: Lineare Regression einfach erklärt
Die Regression setzt eine Zielvariable mit einer oder mehreren unabhängigen Variablen in Beziehung. In der linearen Regression liegt ein linearer Zusammenhang zwischen Zielvariable und Einflussvariablen vor. Mit Hilfe von statistischer Software können anhand vorliegender Daten die Schätzwerte für den Intercept und die Regressionskoeffizienten bestimmt werden. Mit einem t-Test können anschliessend die Regressionskoeffizienten überprüft werden. Das Bestimmtheitsmass R2 liefert ein Gütekriterium, wie gut das Modell die Daten beschreibt. Mit Hilfe einer Varianzanalyse (ANOVA) lässt sich testen, ob das Regressionsmodell die Zielgrösse vorhersagen kann. Als Voraussetzung für die Berechnungen müssen die Residuen dabei voneinander unabhängig, normalverteilt und homoskedastisch sein.
Bei Modellierung mehrerer Einflussvariablen spricht man dann von einer multiplen linearen Regression. Das Modell wird dabei in den n-dimensionalen Raum übertragen.
In diesem Artikel haben wir Ihnen einen Überblick über das Thema Regression gegeben und dabei die lineare Regression einfach erklärt. Sollten sie Rückfragen zu speziellen Aspekten der Regression haben, können sie sich hierzu jederzeit gerne an uns wenden. Bei Fragen oder Problemen rund um Auswertung, Interpretation und allen anderen statistischen Belangen stehen unsere Experten von Novustat Ihnen gerne zur Seite.
