In der inferenziellen Statistik (auch: schliessende Statistik) werden Hypothesen auf eine bestimmte Verteilung, auf einen Zusammenhang und auf einen signifikanten Unterschied innerhalb der betrachteten Merkmale getestet. Wenn man im Rahmen einer Untersuchung der Korrelation SPSS anwendet, dann untersucht man eine Paarung metrisch (kardinal) skalierter Merkmale auf einen Zusammenhang. Nachfolgend erläutern wir zunächst das mathematische Modell. Daraufhin zeigen wir eines Beispiels, wie man für eine Analyse der Korrelation SPSS nutzt.
Sollten Sie Unterstützung bei Ihrer Auswertung mit SPSS benötigen, helfen unsere Statistiker Ihnen gerne weiter. Kontaktieren Sie uns für eine kostenlose Beratung & ein unverbindliches Angebot!
Was Sie bei der Korrelation in SPSS im Hinterkopf behalten sollten
Wichtig ist bei allen Tests auf Zusammenhang, dass es sich lediglich um einen stochastischen Zusammenhang handelt. Man testet also auf Basis statistischer und wahrscheinlichkeitstheoretischer Annahmen. Man kann daher nur die Stärke des Zusammenhangs zwischen metrischen Merkmalen ableiten, nicht aber einen kausalen Zusammenhang.
Die Korrelationsanalyse aus mathematischer Sicht
Bei der Korrelation handelt es sich um die Annahme eines annähernd linearen Zusammenhangs zwischen den Merkmalen. Die Stärke des Zusammenhangs kann positiv oder negativ gerichtet sein. Für die Anaylse der Bedeutung und Interpretation der Art eines funktionalen Zusammenhangs ist eine lineare Regression durchzuführen.
Sie möchten eine Korrelationsanalyse in SPSS durchführen, benötigen aber Hilfe bei der Durchführung oder Interpretation der Daten? Kontaktieren Sie uns für eine professionelle Unterstützung bei der SPSS Auswertung! Unsere Experten sind vertraut mit einer Vielzahl an statistischen Verfahren in SPSS und helfen Ihnen schnell und kompetent weiter.
Für eine Korrelation SPSS nutzend befolgt man gemäss dem mathematischen Ablauf nach Bravais und Pearson drei Schritte:
- 1.Berechnung der Kovarianz der Variablen – CoV(x,y)=E[(x-E(x))(y-E(y))]
Die Kovarianz ist in ihrem Wertebereich unbeschränkt. Deshalb ermöglicht sie nur eine Aussage über Positivität oder Negativität des Zusammenhangs, nicht jedoch über die Stärke. - 2. Berechnung der Standardabweichungen der Variablen und Normierung der Kovarianz – die so berechnete Korrelation nimmt nur noch Werte zwischen -1 und 1 an, was eine Interpretation der Stärke des stochastischen Zusammenhangs ermöglicht.
- 3. Vergleich der errechneten Korrelation zum zu erwartenden quadratischen Fehler – hierbei wird die Abweichung zur Korrelation zweier normalverteilter Merkmale bestimmt und mit den Quantilen der F-Verteilung (f-Test SPSS) verglichen.
Die Korrelation in SPSS
Die Korrelation, SPSS ordnet die Analyse nicht den Mittelwerttests zu, findet sich im Reiter: „Analysieren → Korrelationen → Bivariat“
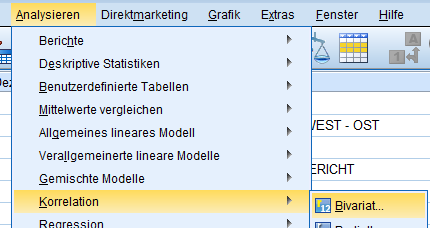
Hier werden die zu untersuchenden Merkmale aus der Liste ausgewählt – wichtig ist hier, dass für die Korrelation SPSS metrisch (kardinal) skalierte Merkmale voreingestellt hat. Als Koeffizient wird der Produkt-Moment-Korrelationskoeffizient nach Pearson verwendet.
Liegt bei zumindest einem Merkmal eine Ordinalskalierung vor und/oder zeigt ein Test auf Normalverteilung SPSS anwendend ein signifikantes Ergebnis, kann von keiner Normalverteilung der Daten ausgegangen werden, so muss in SPSS stattdessen der Rangkorrelationskoeffizient nach Spearman angeklickt werden.
Korrelation SPSS: Ergebnisse erläutert für ein Beispiel
Im angeführten Beispiel – es handelt sich um eine Korrelation SPSS nach Pearson – wird eine Tabelle mit vier Feldern ausgegeben, von denen nur das untere linke und das obere rechte von Interesse sind. In dieser 2×2 Matrix sind die Werte beiden Feldern natürlich ident. Die Werte geben die Korrelation, die Signifikanz und die Anzahl ausgewerteter Paare wider.

Im gewählten Beispiel wurde die Korrelation zwischen dem Nettoeinkommen und der Wahlbeteiligung analysiert – die Korrelation SPSS beträgt laut Ausgabetabelle -0,176, damit kann angenommen werden, dass zwischen der Wahlbeteiligung und dem Nettoeinkommen ein schwacher negativer Zusammenhang besteht.
Der Signifikanztest mit einer p-Wert Statistik von unter 5% zeigt, dass die Nullhypothese verworfen werden kann und es einen hoch signifikanten Zusammenhang zwischen beiden Merkmalen gibt und zwar insofern, als mit steigendem Nettoeinkommen die Wahlbeteiligung sinkt und umgekehrt.
Wenn man für die Korrelation SPSS anwendet, zeigt das Beispiel, dass eine gewählte Merkmalspaarung nicht zwangsläufig einen logischen Zusammenhang aufweisen muss:
Ein deutlicheres Beispiel sind der IQ und die Schuhgrösse – in beiden Fällen handelt es sich um metrisch (kardinal) skalierte Merkmale, allerdings nimmt weder die Schuhgrösse mit dem IQ, noch der IQ mit der Schuhgrösse zu.
Es gilt also: Ein statistisch begründeter (stochastischer) Zusammenhang impliziert keineswegs zwangsläufig einen kausalen Zusammenhang!