Lineare Regressionsanalyse SPSS: Hintergrund & Durchführung
Neben grafischen und numerischen Analysen für unterschiedlich skalierte Erfassungsvariablen bietet die SPSS Software die Möglichkeit, eine Regressionsanalyse für metrische Paarungen von abhängigen und unabhängigen Variablen durchzuführen.
Im Folgenden wird zunächst auf die (mathematischen) Grundzüge eines Regressionsmodells im Allgemeinen eingegangen. Danach wird beschrieben, wie die Anwendung lineare Regression SPSS Version 22 abläuft. (Für ältere Versionen ist der Ablauf ähnlich, die Ausgabeformate können jedoch abweichen.)
Abschliessend werden die Ergebnisse – anhand eines Beispiels zu lineare Regression SPSS anwendend interpretiert und bewertet.
Sollten Sie Unterstützung bei Auswertungen mit SPSS benötigen, helfen unsere Statistiker Ihnen gerne weiter
Für die Regressionsanalyse SPSS nutzen – der mathematische Hintergrund
Bei einer Regression handelt es sich um ein strukturprüfendes Verfahren, mit dem die Art eines Zusammenhangs festgestellt werden kann. Ausgang einer Regressionsanalyse ist die Annahme, dass zwei oder mehr metrisch (kardinal) skalierte Variablen in einem funktionalen Zusammenhang zueinander stehen. Ziel ist es, den Wert von abhängigen Variablen (gemeinhin mit Y bezeichnet) durch unabhängige (erklärende) Variablen (mit X bezeichnet) vorherzusagen.
Sie benötigen Hilfe bei der Durchführung einer Regressionsanalyse in SPSS? Nutzen Sie die SPSS Hilfe durch unsere erfahrenen Experten!
Nun wird angenommen, dass sich Y als f(X) für eine Funktion f schreiben lässt – diese Funktion y=f(x) anhand von Beobachtungsdaten zu schätzen wird als Regression bezeichnet.
Da die beobachteten Daten als Realisation zufälliger Grössen (Ausgangsvariablen und ggf. Basisfehler) aufgefasst werden, muss selbst eine exakte Regression nicht zwangsläufig dem realen ‚wahren‘ Sachverhalt entsprechen.
Zur Bestimmung der Funktionsparameter gibt es verschiedene Ansätze, von denen sich die Methode der kleinsten Quadrate bewährt hat. Zum einen entspricht die quadratische Abweichung dem erprobten Modell der Varianz, die für Verteilungsmodelle relativ einfach zu bestimmen ist. Zum anderen existieren für quadratische Optimierungen bereits numerisch implementierte Algorithmen, auf die in SPSS zurückgegriffen werden kann.
Eine einfache lineare Regression folgt dem Modell Y = a + b*X, wobei a und b die Regressionskoeffizienten darstellen, konkret steht a für die Konstante und b für den Anstieg der Regressionsgeraden.
Ausführlicheres zum Begriff und zum mathematischen Modell finden Sie in unserem Artikel zur Regression in der Statistik.
Lineare Regression SPSS – Die Durchführung
Die lineare Regression SPSS findet sich unter: „Analysieren → Regression → Linear“
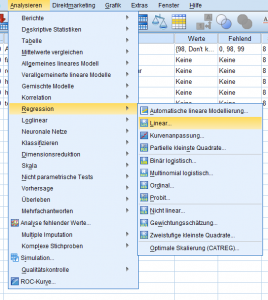
Zunächst gilt zu entscheiden, welcher Funktionstyp zu Grunde gelegt werden soll, ob die Wahl also auf einen linearen Zusammenhang Y = a + b*X fällt oder ob eine logistische oder multinomiale Regression die Basis bildet.
Im zweiten Schritt ist festzulegen, ob das Modell eine oder mehrere unabhängige Variablen erfassen soll, in letzterem Fall ob es sich um mittelbare oder unmittelbare Einflüsse handelt. In SPSS findet dies unter dem ersten Menüpunkt statt – in einem geführten Dialog werden zunächst die Eingangsvariablen und die Zielvariable festgelegt, danach können weitere Modellierungskriterien berücksichtigt werden.
Die einzelnen zu wählenden Regressionsmodelle unterscheiden sich in den jeweiligen Messniveaus der abhängigen bzw. unabhängigen Variablen:
- Lineare Regression SPSS – sie berücksichtigt eine metrisch (kardinal) skalierte abhängige und eine (zumeist) metrisch skalierte (erklärende) unabhängige Variable
- Multiple Regression SPSS – sie berücksichtigt eine metrisch skalierte abhängige und mehrere unabhängige Variablen, die metrisch, ordinal oder dichotom skaliert sein können
- Logistische Regression SPSS– sie berücksichtigt eine dichotome (mit genau zwei Ausprägungen) abhängige und ein oder mehrere unabhängige Variablen mit beliebigem Skalenniveau
- Multinominale logistische Regression SPSS – sie berücksichtigt eine nominal skalierte abhängige Variable mit mehr als zwei Ausprägungen und ein oder mehrere unabhängige Variablen mit beliebigem Skalenniveau
Der Anschaulichkeit halber wird hier die lineare Regression SPSS vorgestellt; die multiple Regression SPSS, logistische Regression SPSS und die multinomiale Regression SPSS laufen vom Prinzip her gleich ab.
Zusätzlich zur analytischen Betrachtung bietet SPSS die Möglichkeit einer grafischen Darstellung, sinnvoll ist hier die Visualisierung mittels Streudiagramm, SPSS ermöglicht dies unter dem Reiter: „Grafik → Diagrammerstellung → Streu-/Punktdiagramm“.
Zieht man die gewünschten (metrischen) Variablen auf die entsprechenden Achsen, wird im Streudiagramm für eine abhängige und eine unabhängige Variable die Punktwolke angezeigt – im Diagrammeditor kann die Darstellung zusätzlich um die Regressionsgerade (auch: Anpassungsgerade genannt) erweitert werden.
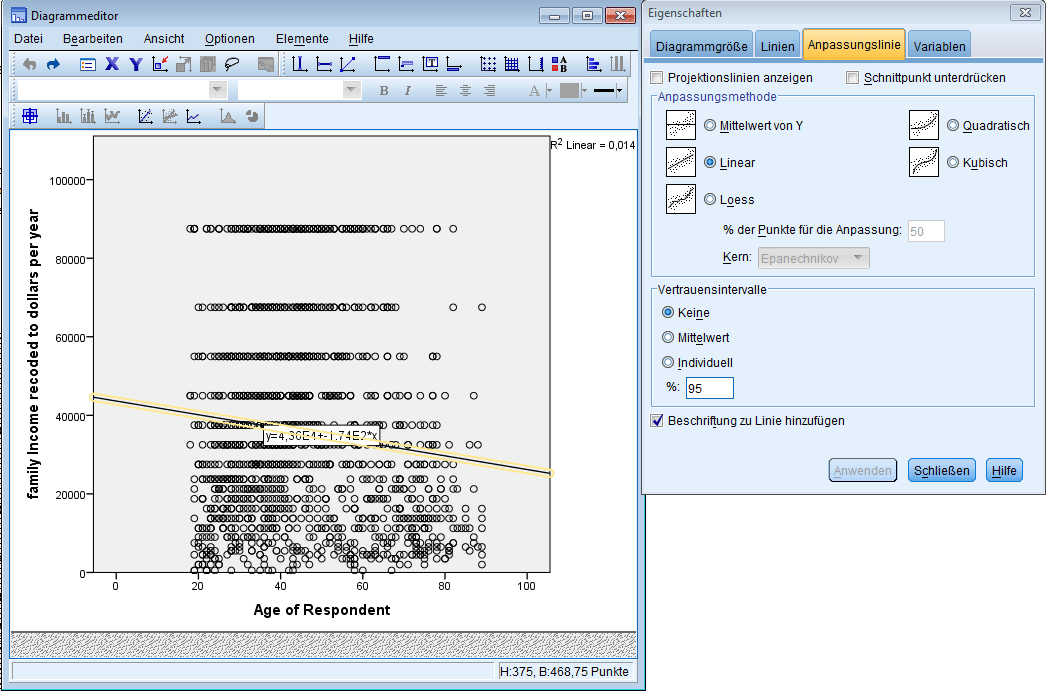
Weiters ermöglicht SPSS die Bestimmung der Modellgüte R^2 sowie der Konfidenzbereiche für die Funktionsparameter zu einem vorher festgelegten Signifikanzniveau (Voreinstellung auf 95%).
Lineare Regression SPSS – Auswertung und Interpretation
Von den ausgegebenen Tabellen ist zunächst die Übersicht der Koeffizienten von Bedeutung.
In der Spalte „nicht standardisierte Koeffizienten“ finden sich unter B die gewünschten Werte.
Im Fall einer linearen Regression sind das ein konstanter (Start-)Wert und die Steigung – wird zum Beispiel das „Alter des Ehemannes“ als unabhängige und das „Haushaltseinkommen pro Jahr“ als abhängige Variable betrachtet, stellt der konstante Wert das Mindesteinkommen bei 0 Lebensjahren dar. Beta repräsentiert dagegen die Zu-/ Abnahme des jährlichen Haushaltseinkommens pro Lebensjahr des Ehemannes.
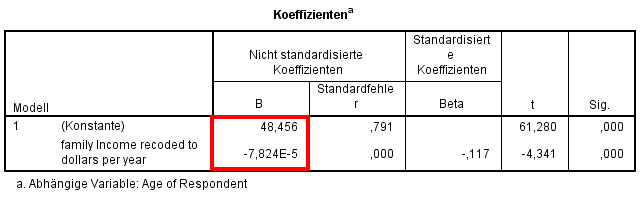
Die rechte Spalte gibt die t-Statistik sowie die zugehörige Signifikanz für die Hypothese Y = a + b*X an. Liegt sie Signifikanz unter 5%, so kann angenommen werden, dass der funktionale Zusammenhang tatsächlich ein linearer ist. Weitere Details zu Signifikanz und p-Wert finden Sie in unserem Glossar-Artikel über die p-Wert Statistik.
Bei der Interpretation ist dennoch Vorsicht geboten – da es sich bei der Regressionsfunktion stets um die Beschreibung zufälliger Grössen handelt, ist ein mathematischer Zusammenhang nicht gleichbedeutend mit einem kausalen. Im voran genannten Beispiel schliesst das Modell andere Einflussfaktoren wie das Einkommen der Ehefrau, Beiträge berufstätiger Kinder und sonstige Einnahmen aus. Ebenfalls vernachlässigt werden die Branche, die Anzahl der Erwerbsjahre oder der Bildungsgrad. Folglich müssten hier zusätzlich Gruppierungen nach den genannten Kriterien erfolgen, was im Zuge einer Varianzanalyse in SPSS erfolgen könnte.
Darüber hinaus könne auch bereits der funktionalen Annahme Schwächen innewohnen – konkretes Beispiel: Werden im Rahmen einer Marktforschungsstudie die Aktivierungsgrade von Probanden untersucht, so haben diese eine natürliche Obergrenze von 100% – jedoch wird diese lediglich von Modellen des begrenzten exponentiellen Wachstums berücksichtigt.
Zusammenfassend gilt es die Ergebnisse kritisch zu interpretieren, da ein statistischer Zusammenhang nicht zwangsläufig einen kausalen Zusammenhang impliziert.
Häufig gestellte Fragen
Was ist eine lineare Regressionsanalyse in SPSS und wie wird sie durchgeführt?
Eine lineare Regressionsanalyse in SPSS ist ein statistisches Verfahren, das die Beziehung zwischen einer abhängigen und einer oder mehreren unabhängigen Variablen untersucht. Die Analyse wird in SPSS durchgeführt, indem man zunächst die Variablen auswählt, dann eine Regressionstabelle generiert und schliesslich die Ergebnisse interpretiert.
Wofür wird eine lineare Regressionsanalyse in SPSS verwendet?
Eine lineare Regressionsanalyse in SPSS kann verwendet werden, um die Stärke und Richtung der Beziehung zwischen einer abhängigen Variablen und einer oder mehreren unabhängigen Variablen zu bestimmen. Sie kann auch dazu verwendet werden, Vorhersagen über die abhängige Variable auf der Grundlage der unabhängigen Variablen zu treffen.
Wie interpretiert man die Ergebnisse einer linearen Regressionsanalyse in SPSS?
Die Ergebnisse einer linearen Regressionsanalyse in SPSS können in einer Regressionstabelle dargestellt werden, die Informationen wie die Koeffizienten, die Signifikanzwerte und die Vorhersagegüte enthält. Die Interpretation hängt von der Fragestellung und den Variablen ab, aber typischerweise sollte man sich auf die Stärke und Richtung der Beziehung sowie auf die Vorhersagegenauigkeit konzentrieren.
Welche Voraussetzungen müssen erfüllt sein, um eine lineare Regressionsanalyse in SPSS durchzuführen?
Vor der Durchführung einer linearen Regressionsanalyse in SPSS müssen einige Voraussetzungen erfüllt sein. Dazu gehören unter anderem die Normalverteilung der abhängigen Variable, die Homoskedastizität und die Unabhängigkeit der Residuen sowie die Linearität der Beziehung zwischen den Variablen.
Wie kann man die Güte einer linearen Regressionsanalyse in SPSS bewerten?
Die Güte einer linearen Regressionsanalyse in SPSS kann anhand mehrerer Kriterien bewertet werden, wie zum Beispiel der Bestimmtheitsmass (R²), der F-Test auf Signifikanz des Modells oder die Standardfehler der Koeffizienten. Eine sorgfältige Interpretation der Ergebnisse in Bezug auf die Fragestellung und die Daten ist jedoch unerlässlich.
Lineare Regressionsmodelle in SPSS belastbar entwickeln.
