Die Survival Analysis ist eine Disziplin innerhalb der Statistik zur Auswertung von zeitabhängigen Ereignissen – das muss aber nicht immer ein Todesfall sein. So setzen wir die Survival Analyse auch ein um z.B. das Auftreten einer Reaktion, Rezidiv oder Remission für unsere Kunden zu modellieren. Innerhalb der Survival Analysis ist die Kaplan-Meier Methode ein wichtiges Verfahren, nicht zuletzt, da die Kaplan Meier Kurve sehr anschaulich Überlebenskurven darstellt. Der Log-Rank-Test dient dazu, Kaplan Meier Kurven miteinander zu vergleichen. Wir zeigen ihnen, wie Daten im Kontext der Survival Analysis korrekt ausgewertet werden. Dabei spielt die Kaplan Meier Kurve und die mediane Überlebenszeit eine Rolle. Der Log-Rank-Test wird verwendet, um unterschiedliche Kaplan-Meier Kurven zu vergleichen.
Gerne stehen wir Ihnen mit unseren Experten mit Rat und Tat bei ihrer Studie zur Verfügung: von einer Statistik-Beratung bis hin zur kompletten Planung, Datenauswertung und Berichterstellung. Nehmen Sie hierzu einfach Kontakt mit uns auf.
Folgende Fragen werden in diesem Artikel beantwortet
- Welche Besonderheiten hat die Survival Analysis?
- Wer oder was ist Kaplan-Meier?
- Wie wird eine Kaplan-Meier-Kurve gezeichnet?
- Was besagt der Log-Rank-Test?
- Wie führe ich eine Survival Analysis nach Kaplan-Meier in SPSS durch?
- Wie wird die Kaplan-Meier Analyse interpretiert?
Zensierung – Warum es unvermeidbar ist, Beobachtungen zu zensieren
Nahezu alle Studien sind aufgrund von ethischen oder ökonomischen Aspekten zeitlich begrenzt. Das heisst aber auch, dass in dem definierten Beobachtungszeitraum nicht immer alle Untersuchungseinheiten Ereignisse haben können. Bei einigen tritt das interessierende Ereignis später auf, bei anderen dagegen nie. Diese Art der Beobachtung wird zensiert genannt. Bei zensierten Beobachtungen liegt „nur“ die Information vor, dass bis zum Studienende das Ereignis nicht eingetreten ist. Das ist immerhin schon eine ganze Menge Information. Zensierte Beobachtungen zu löschen oder mit fehlenden Werten gleichzusetzen verzerrt deshalb die Ergebnisse. Kaplan & Meier haben darum 1958 ein Verfahren entwickelt, zensierte Beobachtungen zu berücksichtigen.
Survival Analysis nach Kaplan-Meier
Bei dieser Art von Survival Analysis wird für jeden Zeitpunkt der Prozentsatz der Patienten berechnet, die noch unter dem Risiko eines Ereignisses stehen. Zu Beginn der Studie, also zum Zeitpunkt 0 hat noch keine Beobachtungseinheit ein Ereignis. Bei 100% der Studienteilnehmer besteht also noch die Möglichkeit, ein Ereignis zu beobachten. Der Wert reduziert sich jedoch bei jedem folgenden beobachteten Ereignis.
Am einfachsten wird dieses Vorgehen anhand eines Beispiels deutlich.
Beispiel: Rauchentwöhnung à la Trude Trugschluss
Die Wunderheilerin Trude Trugschluss hat eine Therapie zur Rauchentwöhnung entwickelt, die sie nun entsprechend bewerben möchte: Sie legt Raucherinnen oder Rauchern, die den starken Wunsch haben, dieses Laster loszuwerden, ihre Hände für 5 Minuten auf den Kopf. Um den Erfolg ihrer Methode zu untermauern, führt sie eine Studie mit 10 Rauchern durch. 7 Teilnehmer haben dabei innerhalb von 12 Stunden nach der Behandlung nicht mehr geraucht. „Das ist ja toll! Eine Erfolgsquote von 70% – UNGLAUBLICH! “.
Unglaublich ist diese Behauptung in jedem Fall. Frau Trugschluss hätte allerdings besser die Hilfe eines Statistikers in Anspruch genommen. Denn nicht nur die kleine Fallzahl mit n=10, sondern auch die extrem kurze (rauchfreie) Beobachtungszeit von 12 Stunden nach der Behandlung lassen Zweifel an der Aussagekraft der Studie entstehen. Der grundsätzliche Fehler von Frau Trugschluss besteht allerdings darin, dass sie die Zeit bis zum Auftreten eines Ereignisses – in diesem Fall das erneute Rauchen – komplett ignoriert.
Zweifel an Trudes Studie
Heinz, ein Statistiker und selbst Raucher, wird auf die Werbeaktion von Trude Trugschluss aufmerksam. Bevor er sich selbst in Behandlung von Trude gibt, hinterfragt er die Hintergründe der von Trude durchgeführten Studie. Dafür fordert er von Trude die Daten an sowie die Zeiten, nach denen ihre Klienten rückfällig geworden sind. Dabei stellt sich heraus, dass Trude Trugschluss ihre 10 Klienten 4 Tage (nach)beobachtet hat und dabei folgende Werte erhoben hat:
| KlientID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Rückfall | ja | nein | ja | ja | ja | ja | nein | ja | ja | ja |
| Beobachtungszeit in Stunden | 6 | 96 | 20 | 9 | 15 | 2 | 30 | 25 | 48 | 62 |
Der erste Klient zündete sich also eine Zigarette 6 Stunden nach Behandlungsende an. Der zweite behandelte Hilfesuchende war dahingegen 96 Stunden nach dem Handauflegen immer noch rauchfrei. Trudes Behandlung wirkte bei Klient Nr. 3 genau 20 Stunden bis zum Rückfall, bei Klient 5 nur 9 Stunden.
„Nun ja“, denkt sich der Statistiker, „Trudes Werbeaktion ist nur die halbe Wahrheit: Anhand der Daten kann man durchaus sagen, dass nach 12 Stunden bei 3 der 10 Klienten ein Rückfall eingetreten ist. Allerdings…“
Trudes Studie löst sich in Rauch auf
…Allerdings hat Trude nur einen kleinen Teil der zur Verfügung stehenden Information verwendet. Der Beobachtungszeitraum wurde (vorsätzlich?) verkürzt, die Zeit bis zum Eintreten des Rückfalls also gar nicht berücksichtigt.
Heinz führt die deshalb Berechnungen mit der Survival Analysis nach Kaplan-Meier durch. Dabei geht er wie folgt vor:
1. Ordnen der Beobachtungszeiten
| KlientID | Rückfall | Beobachtungszeit in Stunden |
| 6 | ja | 2 |
| 1 | ja | 6 |
| 4 | ja | 9 |
| 5 | ja | 15 |
| 3 | ja | 20 |
| 8 | ja | 25 |
| 7 | nein | 30 |
| 9 | ja | 48 |
| 10 | ja | 62 |
| 2 | nein | 96 |
2. Bestimmung der Anzahl der unter Risiko für ein Ereignis (Rückfall Rauchen) stehenden Klienten
| KlientID | Rückfall | Beobachtungszeit in Stunden | Anzahl unter Risiko stehender Klienten |
| 6 | ja | 2 | 10 |
| 1 | ja | 6 | 9 |
| 4 | ja | 9 | 8 |
| 5 | ja | 15 | 7 |
| 3 | ja | 20 | 6 |
| 8 | ja | 25 | 5 |
| 7 | nein | 30 | 4 |
| 9 | ja | 48 | 3 |
| 10 | ja | 62 | 2 |
| 2 | nein | 96 | 1 |
3. Berechnung des Kaplan-Meier Schätzers
| KlientID | Rückfall | Beobachtungszeit in Stunden | Anzahl unter Risiko stehender Klienten | Kaplan-Meier Schätzer |
| 6 | ja | 2 | 10 | 9/10 = 90% |
| 1 | ja | 6 | 9 | 9/10*8/9 = 80% |
| 4 | ja | 9 | 8 | 9/10*8/9*7/8 = 70% |
| 5 | ja | 15 | 7 | 9/10*8/9*7/8*6/7 = 60% |
| 3 | ja | 20 | 6 | 9/10*8/9*7/8*6/7*5/6= 50% |
| 8 | ja | 25 | 5 | 9/10*8/9*7/8*6/7*5/6*4/5 = 40% |
| 7 | nein | 30 | 4 | 40% |
| 9 | ja | 48 | 3 | 40%*2/3=26,7% |
| 10 | ja | 62 | 2 | 26,6%*1/2=13,3% |
| 2 | nein | 96 | 1 | 13,3% |
Nach 2 Stunden raucht der erste Klient wieder. Die Wahrscheinlichkeit bis zum Ende der zweiten Stunde rauchfrei zu bleiben beträgt also 9/10=90%.
Nach 6 Stunden wird dann der nächste Klient rückfällig. Die Wahrscheinlichkeit, von der 2. Stunde bis zur 6. Stunde rauchfrei zu bleiben beträgt also 8/9. Die Wahrscheinlichkeit, vom Stunde Null (Handauflegen) bis zur 6. Stunde rauchfrei zubleiben ergibt sich als Produkt der vorhergehenden Wahrscheinlichkeiten, also 90%*8/9 = 80%.
Nach 9 Stunden beobachtet man das nächste Ereignis. Die Wahrscheinlichkeit länger als 9 Stunden durchzuhalten beträgt 70%, länger als 15 Stunden durchzuhalten 60% usw. Nach einer Beobachtungszeit von 30 Stunden tritt schliesslich eine Zensierung auf. Der Klient mit der ID 7 hat bis zu diesem Zeitpunkt nicht geraucht. Bis zu diesem Zeitpunkt wurde diese Information deshalb in der Berechnung der Wahrscheinlichkeiten berücksichtigt. Für die weiteren Berechnungen kann er aber nicht mehr herangezogen werden, weil über sein weiteres Rauchverhalten über die 30 Stunden hinaus nichts bekannt ist. Die Anzahl der unter Risiko stehenden Klienten reduziert sich deshalb um 1. Der Kaplan-Meier Schätzer bleibt konstant, da kein Ereignis eingetreten ist.
Zum nächsten Zeitpunkt, nach 48 Stunden tritt aber ein neuerlicher Rückfall auf. Die Wahrscheinlichkeit, zwischen 30 und 48 Stunden keinen Rückfall zu haben beträgt daher 2/3. Dadurch ergibt sich der Kaplan-Meier Schätzer als 40% * 2/3=26,7%.
Berechnung mit SPSS
Natürlich kann man die Berechnung auch mit Software durchführen. In SPSS gibt man dazu zunächst die Daten in das Datenfenster ein.
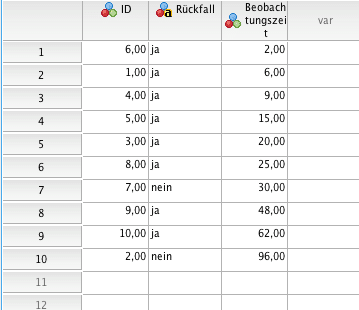
Anschliessend wählt man Analysieren – Überleben – Kaplan-Meier.
Als Zeitvariable wird dann die Beobachtungszeit angegeben. Bei Status gibt man die Variable an, die kennzeichnet, ob der Klient zensiert ist. Dazu muss man bei Ereignis definieren festlegen, mit welchem Wert das Ereignis kodiert ist.
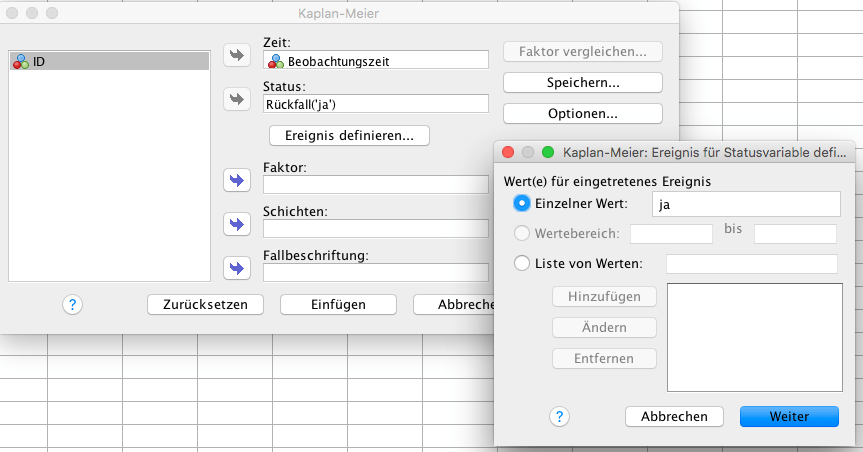
Hat man diese Angaben gemacht, kann die Auswertung schliesslich mit OK bestätigt werden.
Im Ausgabefenster erscheint darauf folgende Auswertung:
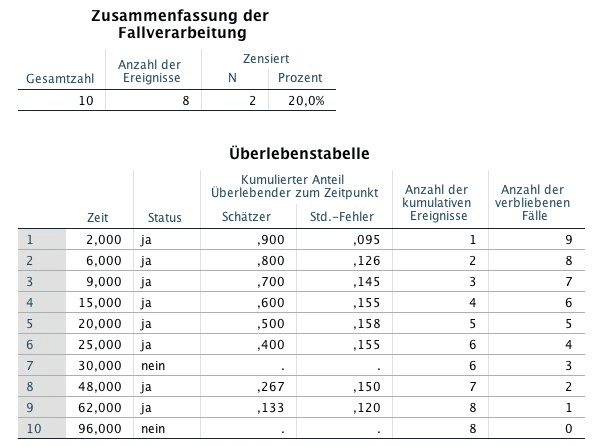
Die erste Tabelle enthält eine Übersicht aller verarbeiteten Datensätze. In der zweiten Tabelle der SPSS Ausgabe wird der Kaplan-Meier Schätzer sowie dessen Standardfehler angegeben.
Kaplan-Meier Kurve
Die Kaplan-Meier Schätzer werden für jeden Beobachtungszeitpunkt berechnet und sind bei grossem Stichprobenumfang meist schwer zu fassen. Aus diesem Grund werden die Kaplan-Meier Schätzer gerne in einem Schaubild dargestellt. Diese Grafik wird Kaplan Meier Kurve oder Überlebenszeitkurve genannt. In SPSS kann diese Art der Darstellung im Kaplan-Meier Menü unter Optionen angefordert werden.
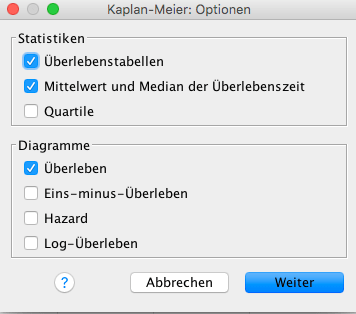
Das Diagramm wird anschliessend im Ausgabefenster dargestellt. Auf der x-Achse ist die Beobachtungszeit abgetragen. Die y-Achse enthält dagegen die mit dem Kaplan-Meier Verfahren berechneten Überlebenswahrscheinlichkeiten.
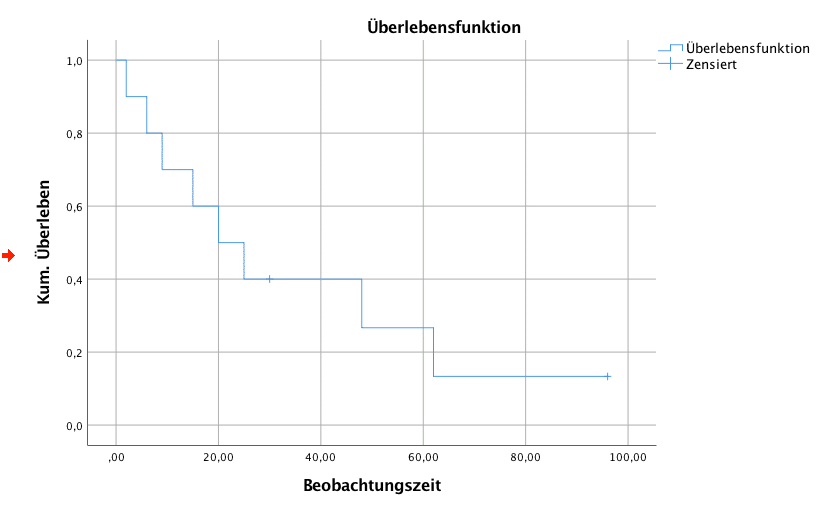
Die Kaplan Meier Kurve startet im Punkt (0,1). Zu Studienbeginn stehen alle Beobachtungseinheiten unter dem Risiko ein Ereignis zu bekommen. Bei jedem beobachteten Ereignis macht die Kaplan Meier Kurve einen Sprung nach unten. Zensierte Klienten sind durch einen senkrechten Strich gekennzeichnet.
„Rauchfrei“-Raten oder doch Überlebensraten?
Anhand der Kaplan Meier Kurve lassen sich leicht Überlebensraten bzw. in unserem Beispiel die „Rauchfrei-Rate” bestimmen. Die auf der y-Achse abgetragene kumulierte Überlebensrate gibt dabei an, bei wie vielen Klienten bis zu einem Zeitpunkt noch kein Ereignis eingetreten ist. Für die Bestimmung der 24-Stunden „Rauchfrei-Rate” müsste man also zum Zeitpunkt 24 Stunden eine Senkrechte zur Kaplan-Meier Kurve ziehen und kann dort die „Rauchfrei-Rate” ablesen, in dem man den Wert auf der y-Achse bestimmt.
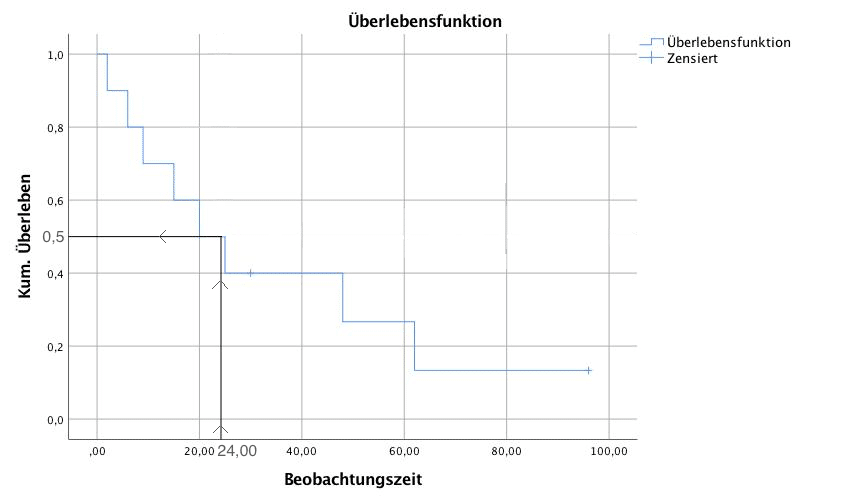
In der Kaplan-Meier Kurve erkennt man, dass 24 Stunden nach der Behandlung von Trude Trugschluss noch (nur?) 50% der Behandelten rauchfrei sind. Nach 48 Stunden beträgt die “Rauchfrei-Rate” sogar nur 26,7%. Bei der Angabe von solchen Raten ist es wichtig, immer den zugehörigen Zeitpunkt zu nennen.
Mediane rauchfreie Zeit (mediane Überlebenszeit)
Die Kaplan Meier-Kurve kann man aber auch umgekehrt interpretieren. Denn sehr häufig wird als Kenngrösse auch die mediane Überlebenszeit angegebene. Darunter versteht man den Zeitpunkt, zu dem die Hälfte der Klienten einen Rückfall oder ein Ereignis erlitten hat. Dazu wählt man auf der y-Achse den Punkt 0,5 (=50%) aus und zieht eine waagrechte Linie zur Kaplan Meier Kurve. Am Schnittpunkt kann man dann die x-Koordinate ablesen.
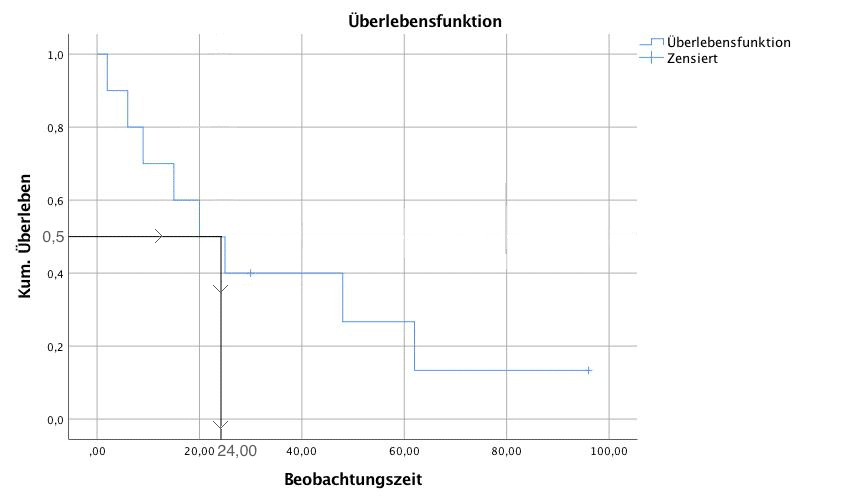
Die mediane Überlebenszeit bzw. mediane ereignisfreie Zeit kann man nur bestimmen, falls der Kaplan-Meier Schätzer unter 0,5 fällt. Falls im Beobachtungszeitraum bei weniger als 50% der Klienten ein Ereignis eingetreten ist, kann die mediane Überlebenszeit nicht angegeben werden.
Als Alternative zur medianen Überlebenszeit wird irrtümlich manchmal statt der medianen Überlebenszeit die mittlere oder durchschnittliche Überlebenszeit angegeben. Diese Masszahl ist aber bei Vorliegen von Zensierungen unbrauchbar und nicht mehr zu interpretieren. Vorsicht ist vor allem deshalb geboten, da diese Masszahl standardmässig von vielen Programmen berechnet wird.
Fortführung: Was nun?
Es hat sich zunächst gezeigt, dass eine Beurteilung des Therapieerfolgs nur mit Einbeziehung der Ereigniszeiten erfolgen kann, die über einen festgelegten, ausreichend langen Beobachtungszeitraum gesammelt werden. Mit diesen Informationen erkennt man, dass 48 Stunden nach der Therapie von Trude Trugschluss (nur) 26,7%, also etwa ein Drittel der Klienten noch rauchfrei sind. Die Hälfte der Patienten wird sogar innerhalb der ersten 24 Stunden nach der Therapie rückfällig.
Die entscheidende Frage ist bislang allerdings noch nicht geklärt: Ist die Therapie Erfolg versprechend? Oder anders ausgedrückt: Soll sich der Statistiker für viel Geld der Behandlung von Trude unterziehen, um mit dem Rauchen aufzuhören?
Ist die Therapie Erfolg versprechend?
Um diese Frage zu beantworten, fehlt etwas sehr Entscheidendes: Die Vergleichsgruppe!
Denkbar wäre beispielsweise eine Gruppe von Rauchern, die ohne Therapie aufhören möchte zu rauchen, eine Placebogruppe (z. B. Auflegen von Händen ohne magische Kräfte) oder einer alternativen Therapie.
Heinz fragt daher in einem rauchfrei-Forum nach, wie lange es dauerte, bis sich die Forumsmitglieder nach dem Jahreswechsel wieder die erste Zigarette anzündeten. (Natürlich muss die Kontrollgruppe bereits im Vorfeld definiert und festgelegt werden und den gleichen Beobachtungszeitraum haben. Hier sollen die Informationen nur als Vergleich mit Trudes Therapie dienen).
Aus den Antworten der Forumsmitglieder generiert Heinz dann die folgende Tabelle:
| ID | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Rückfall? | ja | ja | ja | nein | ja | ja | ja | ja | nein | nein | nein |
| Zeit bis Rückfall in Stunden | 1 | 8 | 10 | 24 | 26 | 34 | 60 | 60 | 69 | 78 | 240 |
Ergänzt man die SPSS Tabelle von Trudes Daten darauf mit diesen Informationen so erhält man folgende Tabelle:
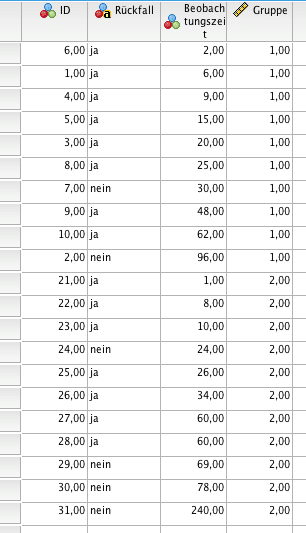
Der Log-Rank-Test – Vergleich zweier Behandlungsgruppen
Der Vergleich zweier Behandlungsgruppen erfolgt erst grafisch anhand der Kaplan Meier Kurve. Die Kurven beider Behandlungsgruppen werden dabei in ein Diagramm abgetragen. Um die ereignisfreien Zeiten inferenzstatistisch miteinander zu vergleichen, wird dann der Log-Rank-Test angewendet. Dieser Test untersucht, ob die ereignisfreien Zeiten zweier Gruppen über den gesamten Beobachtungszeitraum gleich sind. Einfach ausgedrückt untersucht der Test dabei die Frage (Nullhypothese): Sind die beiden Kaplan-Meier Kurven gleich?
In SPSS muss erst die Gruppenvariable in das Feld Faktor gegeben werden. Anschliessend lässt sich der Log-Rank-Test über die Schaltfläche Faktor vergleichen... auswählen.
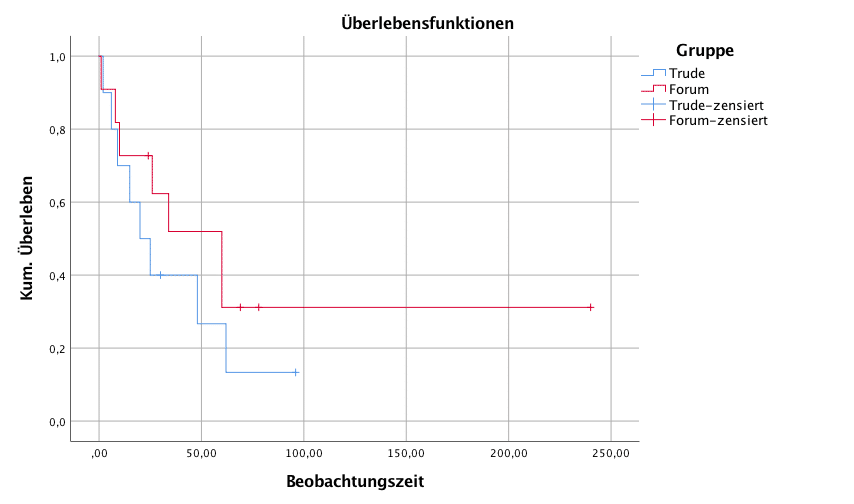
In der Grafik erkennt man, dass die rote Kurve, die die Forumsgruppe darstellt über der von Trudes Gruppe liegt. Insgesamt sieht es so aus, dass die Zeit bis zum ersten Rückfall im Forum etwas länger dauert als nach Trudes Behandlung. Kann man bei 21 Beobachtungen solche Kurvenunterschiede auch zufällig erhalten, wenn tatsächlich die beiden Behandlungen in Wahrheit äquivalent sind? Dazu muss man den Log-Rank-Test heranziehen.

Mit einem p-Wert von 0,324 (Spalte Sig.) kann ein Unterschied zwischen den beiden Behandlungsmethoden statistisch nicht nachgewiesen werden (Signifikanzniveau 5%). Das wiederum bedeutet, dass Trudes Therapie weder besser noch schlechter als Eigeninitiative ist. „Wunderbar“, denkt sich Heinz darauf und wirft den Werbeflyer in den Papiercontainer.
Zusammenfassung
Die Survival Analysis oder Ereignisanalyse ist in vielen Bereichen relevant, insbesondere in der Biostatistik. Neben dem Tod im engeren Sinn nutzen wir die Survival Analysis, um für unsere Kunden das erste Auftreten von beliebigen Ereignissen zu modellieren. Dazu gehören z. B. Rezidive, Entdeckung von Metastasen aber auch positive Ereignisse wie die Geburt eines Kindes nach einem festgelegten Startpunkt oder das Erreichen eines festgelegten Umsatzes. Dabei wird in der Survival Analysis immer die Zeit bis zum Auftreten des Zielereignisses modelliert. Zensierte Daten müssen dabei unbedingt berücksichtigt werden.
Nur durch die Verwendung aller zur Verfügung stehender Informationen, der Anwendung geeigneter Methoden und dem verantwortungsvollen und umsichtigen Umgang können schliesslich korrekte Schlussfolgerungen erfolgen.
Unsere Experten stehen Ihnen in allen Fragen rund um die Datenanalyse zur Verfügung. Nehmen Sie hierzu Kontakt auf!
Weiterführende Informationen
Übersichtsarbeit zur Survival Analysis, deutsches Ärzteblatt
Kaplan-Meier Kurven und die Hazard Ratio
Seriöse Hilfestellung für rauchfreies Leben gibt es bei der BZgA
