Bei Texten über klinische Studien fallen häufig die Begriffe Odds Ratio und relatives Risiko. Beinhaltet die Studie eine Survival Analyse, so wird oft auch die Kennzahl des Hazard Ratio angegeben. All diese Grössen geben eine Verhältnismässigkeit verschiedener Risiken an. In diesem Artikel wollen wir die Zusammenhänge und Unterschiede der genannten Kennzahlen beleuchten.
Sie möchten eine Risikoanalyse durchführen und benötigen dafür Unterstützung oder benötigen Statistik Hilfe für die Anwendung und Interpretation der Kennzahlen? – dann wenden sie sich hierzu an uns für eine professionelle Beratung!
Der folgende Artikel geht zunächst auf das Relative Risiko ein. Anschliessend diskutieren wir das Odds Ratio und zum Abschluss behandeln wir noch das Hazard Ratio in Verbindung mit einer Kaplan-Meier Kurve. Ergänzen werden wir die Erläuterungen mit praktischen Anwendungsbeispielen.
Das Relative Risiko: Eine unerreichbare Grösse?
Das Relative Risiko (kurz RR, auch Risikoverhältnis genannt) lässt sich noch am ehesten intuitiv verstehen. Es beantwortet die Frage „Wie viel wahrscheinlicher tritt Ereignis B ein, wenn vorher Ereignis A eingetreten ist?“
Zur Veranschaulichung ziehen wir Daten heran, die eine Impfung (Ereignis A) und eine Erkrankung (Ereignis B) protokollieren. Insgesamt wurden 1.000 Personen den Krankheitserregern ausgesetzt. Von denen sind 50 % bereits geimpft.
Von den Geimpften infizierten sich 30 Personen. Bei den Ungeimpften waren es 110. Die folgende Tabelle veranschaulicht die Daten:

Wir errechnen nun das Verhältnis aus den jeweiligen Infektionsrisiken:
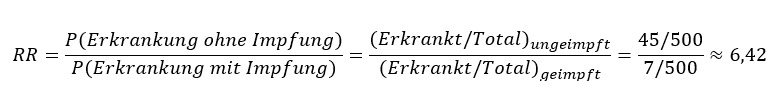
Es ist also etwa 6,5-mal wahrscheinlicher sich zu infizieren, wenn man die Impfung vorab nicht verabreicht bekommen hat.
Hier ist wichtig zu verstehen: auch unabhängig von der gewählten Anzahl an Probanden (dh. wenn nicht wie im fiktiven Beispiel oben exakt 500 Personen bereits geimpft sind) besteht ein deutlich höheres Infektionsrisiko bei Nicht-Geimpften.
Wichtig ist jedoch zu wissen, wie gross die Gesamtgruppe (Grundgesamtheit, Population) ist, hier: 1.000 Personen, die den Krankheitserregern ausgesetzt war.
Klarheit schaffen mit dem Odds Ratio
Und eben an der Stelle kommt das Odds Ratio ins Spiel: Für die Interpretation von Odds Ratio ist es ausreichend zu wissen, wie gross unsere Stichprobe ist bzw. viele Personen wir untersuchen/interviewen.
Ein exaktes Wissen der Populationsgrössen (Grundgesamtheit) ist damit nicht Voraussetzung.
Vielmehr wird mit Odds Ratio (OR) ein Verhältnis der jeweiligen Untergruppen („Erkrankt“ und „Nicht erkrankt“) gebildet. Die Berechnung mit den Daten der obigen Tabelle sieht somit wie folgt aus:
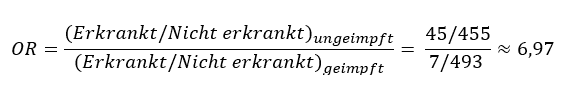
Das Ergebnis ist nun ähnlich dem des Relativen Risikos. Das gilt generell, wenn es sich bei um ein seltenes Ereignis (hier: Erkrankung) handelt (Rare Disease Case).
Das ist auch der Vorteil des Odds Ratio: Im Fall eines seltenen Ereignisses können wir mit dem Odds Ratio aus einer Stichprobe der Gesamtbevölkerung eine gute Schätzung für das Relative Risiko der Grundgesamtheit erreichen.
Stellen wir uns vor, wir fragen analog dem obigen Beispiel jeweils 50 erkrankte und 50 gesunde Personen nach deren Impfstatus:

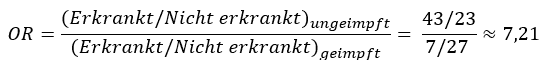
Wir erkennen auf den ersten Blick, dass wir uns auch aus einer sehr kleinen Stichprobe – und ohne Kenntnis der Grösse der Gesamtpopulation – dem Relativen Risiko gut annähern. Sprich: Je seltener das Ereignis, desto genauer die Annäherung von OR und RR.
Was die Interpretation des Odds Ratio betrifft, bestätigt sich also die Annahme, dass es sich eine gute Annäherung für das Risk Ratio, also das Relative Risiko, handelt.
Kaplan-Meier Kurve und Hazard Ratio: Wie passt das zusammen?
Die oben genannten Masse sind stets abhängig vom konkreten Zeitpunkt, an dem die Erhebung durchgeführt wird. Folglich werden diese sich auch ändern, wenn man die Befragung der Studienteilnehmer zu einem anderen (früheren oder späteren) Zeitpunkt vornimmt.
Möchte man eine zeitunabhängige Darstellung für das Risiko eines Ereignisses (z.B. Krankheit) unter Berücksichtigung einer möglichen Einflussvariable (z.B. Geschlecht), bieten sich Kaplan-Meier Kurven und das Hazard Ratio an. Diese sind Teil der sogenannten Survival- bzw. Überlebensanalyse.
Wir wollen mit R einen Datensatz (‘Cancer‘, Datensatz findet sich im Anhang) untersuchen. Die folgenden Codezeilen geben alle Schritte wieder, die benötigt werden, um die unten abgebildete Kaplan-Meier Kurve darzustellen.
Näheres zu statistischer Programmierung zu R finden Sie in unseren Einsteigerartikeln zu Regression in R und ggplot2: Grafiken in R.
```{r}
library(survival)
library(tidyverse)
library(ggfortify)
data(cancer)
head(cancer)
km <- with(cancer, Surv(time, status))
km_sex_fit <- survfit(Surv(time, status) ~ sex, data=cancer)
autoplot(km_sex_fit)
```
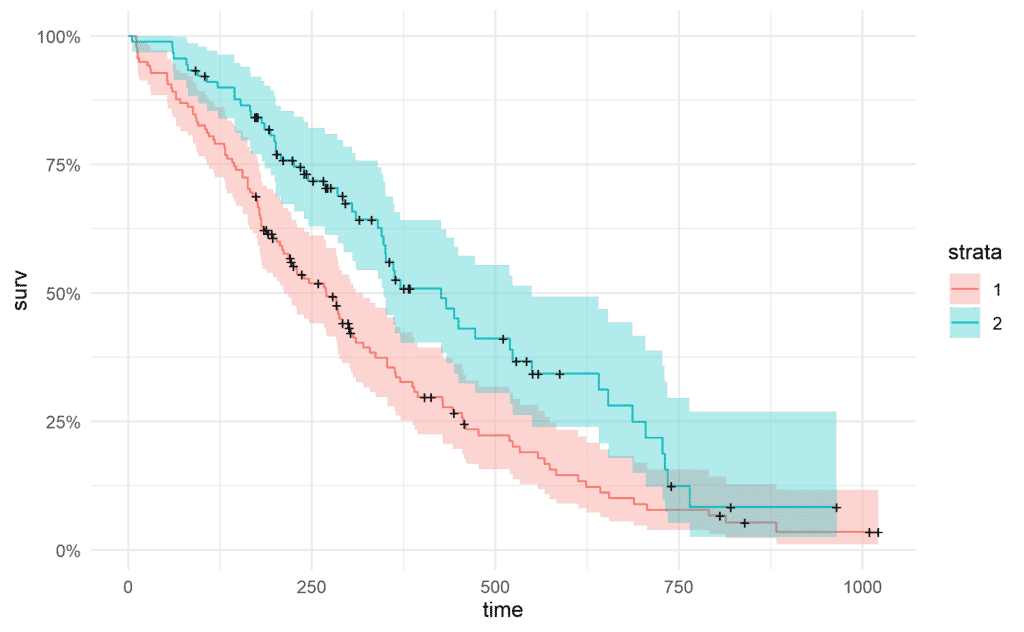
Eine Kaplan-Meier Kurve gibt zu jedem Zeitpunkt (hier: angegeben in Tagen nach Beginn der Studienteilnahme) die Überlebenswahrscheinlichkeit der Gruppenangehörigen (männlich, weiblich) in Prozent an. Schnell wird klar, dass man hier weder Odds Ratio noch Risk Ratio bestimmen kann.
Man müsste sich dafür nämlich für einen bestimmten Zeitpunkt entscheiden. An dieser Stelle kommt das Hazard Ratio ins Spiel: Genau genommen muss eine sogenannte Cox Regression durchgeführt werden. Die Details des Cox Proportional Hazard Models sind sehr umfangreich und tiefgehend.
Hazard Ration und Cox Regression
An dieser Stelle sei daher nur so viel gesagt: Die Cox Regression gibt in Abhängigkeit der unabhängigen Variablen (hier: Geschlecht und Zeit) die Hazard Rate h(t) an. Dazu werden Koeffizienten b1 zur Einflussvariable Geschlecht und das Baseline Hazard h0(t) bestimmt. konkret:
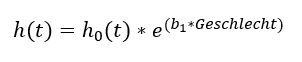
Dann gibt eb1 das Hazard Ratio für Geschlecht an. Es handelt sich um einen zeitunabhängigen Parameter, der das Verhältnis des Erkrankungsrisiko zwischen zwei Gruppen angibt. In anderen Worten wird der Unterschied zwischen den beiden Kaplan-Meier Kurven quantifisiert.
In R können wir mit folgendem Code ein solches Cox Proportional Hazard Ratio erstellen:
```{r}
cox_model <- coxph(Surv(time, status) ~ sex, data = cancer)
summary(cox_model)
```
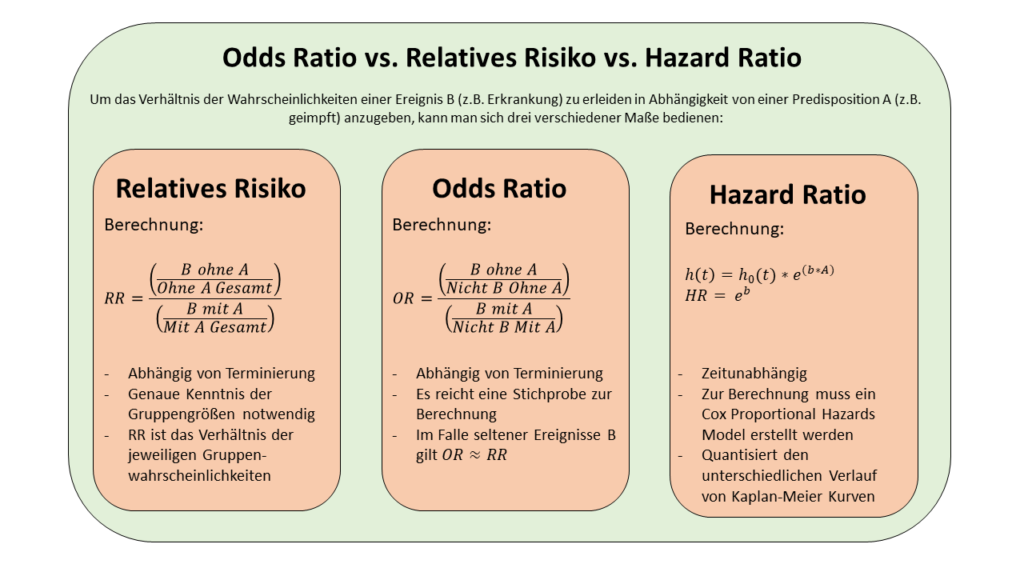
Zusammenschau: Odds Ratio vs. Releatives Risiko vs. Hazard Ratio
In der Zusammenfassung lässt sich ablesen, dass das Hazard Ratio (exp(coef)) gleich 0,588 ist. Das bedeutet als Frau hat man nur ein ca. 59 % Risiko an der Krankheit zu sterben, wie als Mann.
Fazit
Je nach Situation, Datenlage und Forschungsfrage können wir uns unterschiedlicher Masse für das das Verhältnis der Gruppenwahrscheinlichkeiten bedienen. Das Relative Risiko ist sozusagen das genaue Mass für den Risikounterschied.
Das Odds Ratio berechnen wir aus einer Stichprobe und bietet einen guten Schätzer für das Risk Ratio. Das Hazard Ratio schliesslich liefert eine zeitunabhängige Vergleichsgrösse.
Damit haben wir mit diesem Artikel einen Überblick über die Interpretation von Odds Ratio, Relatives Risiko (Risk Ratio) und Hazard Ratio gegeben.
Bei weiteren Fragen und Unterstützungsbedarfen freuen wir uns über Ihre unverbindliche Kontaktaufnahme über unser Anfrageformular. Gerne erstellen wir Ihnen umgehend unverbindlich ein massgeschneidertes Angebot!