Professionelle statistische Versuchsplanung: Mit dem unvollständigen Versuchsplan zum Erfolg

Studenten und Doktoranden der Naturwissenschaft stehen oftmals vor der Situation, im Rahmen ihres Studiums Experimente durchführen zu müssen. Die statistische Versuchsplanung ist hierbei entscheidend, jedoch fehlt vielerstelle das entsprechende Wissen. Auch später im Berufsleben müssen die Experimente vor ihrer Durchführung gründlich geplant werden. Sind Sie beispielsweise ein Ingenieur und möchten Produkte und Fertigungsprozesse optimieren, dann sollten Sie gewisse Grundkenntnisse über die statistische Versuchsplanung besitzen. Denn eine solide Versuchsplanung spart Geld und Zeit und ermöglicht eine langfristige Effizienzsteigerung in der Produktion. Als Mediziner möchten Sie aus ethischen Gründen mit einer möglichst kleinen Anzahl an Probanden auskommen und dennoch wichtige Erkenntnisse über ein neues Medikament gewinnen. Und selbst die Psychologie beschränkt sich nicht nur auf Fragebögen, sondern führt auch Experimente durch.

Damit Sie mit Ihrem Experiment alle gewünschten Ziele erreichen, unterstützt Sie unser Team mit seiner statistischen Versuchsplanung. Sie profitieren vom Know-How von unseren 80 akademischen Statistikern, die täglich statistische Projekte planen, diese durchführen und auswerten. Nutzen Sie einfach unser Kontaktformular für eine kostenlose Beratung & ein unverbindliches Angebot – oder rufen Sie uns an.

In diesem Artikel erhalten Sie Tipps für die professionelle statistische Versuchsplanung. Benötigen Sie hingegen lieber Tipps, wie Sie Ihre Umfrage auswerten, haben wir auch dafür einen passenden Blog-Artikel erstellt.

Statistische Versuchsplanung: Welchen Versuchsplan soll ich wählen?

Die Vielzahl statistischer Versuchspläne lässt sich grob in zwei Kategorien gliedern, vollständige und unvollständige Versuchspläne. Möchten Sie alle Kombinationen an Faktorstufen in Ihrem Experiment testen, führen Sie einen vollständigen Versuchsplan durch. Bei einem Faktor A mit den fünf Stufen a₁, a₂, a₃, a₄ und a₅ sind also fünf Einzelversuche durchzuführen. Kommt nun ein weiterer Faktor B mit den fünf Stufen b₁, b₂, b₃, b₄ und b₅ hinzu, werden alle Stufen des Faktors A mit allen Stufen des Faktors B kombiniert. Die Versuchsplanung enthält also die 5*5 = 25 Kombinationen (a₁,b₁), (a₁,b₂), (a₁,b₃) und so weiter an Faktorstufen. Durch die Hinzunahme eines weiteren Faktors C mit fünf Stufen muss man sogar insgesamt 5*5*5 = 125 Einzelversuche durchführen. Möchten Sie einen vollständigen Versuchsplan erstellen, müssen Sie also berücksichtigen, dass der Stichprobenumfang exponentiell anwächst – und zwar mit jedem zusätzlichen Faktor und jeder zusätzlichen Faktorstufe. Das ist aus finanziellen und zeitlichen Gründen oftmals nicht durchführbar. Doch zum Glück bietet die Versuchsplanung eine Alternative zur Verfügung – den unvollständigen Versuchsplan. Beim unvollständigen Versuchsplan wird die große Anzahl an Faktorstufenkombinationen systematisch reduziert und zwar ohne dass es zu verzerrten Schätzungen der Effekte oder anderen Nachteilen kommt. Ein besonderer unvollständiger Versuchsplan ist der balancierte unvollständige Versuchsplan (englisch: BIBD = Balanced Incomplete Block Design), welcher neben einem Blockfaktor einen weiteren (den interessierenden) Faktor beinhaltet. Im folgenden Abschnitt erfahren Sie anhand eines Praxisbeispiels, wie Sie mit der Statistik-Software R die statistische Versuchsplanung durchführen und so einen balancierten unvollständigen Versuchsplan erhalten. Im Anschluss werden dann die Besonderheiten dieses Versuchsplans erläutert.

Wie kann ich einen balancierten unvollständigen Versuchsplan erstellen?

Angenommen, Hautkrebsforscher möchten drei verschiedene Sonnencremes testen. Dazu werden auf die Oberseiten der Hände eines Probanden zwei verschiedene Sonnencremes aufgetragen. Nach einer Bestrahlung durch UV-Licht werden anschließend die Hautschädigungen in Form von Sonnenbrand protokolliert.

Die linke und rechte Hand der Probanden bilden die Versuchsobjekte innerhalb eines Blocks (ein Block ist ein Proband in diesem Beispiel). Durch die Berücksichtigung des Blockeffekts ist es möglich davon auszugehen, dass beide Hände einer Person die identische Eigenschutzzeit aufweisen und eventuelle Unterschiede in der anschließenden Hautrötung tatsächlich auf die unterschiedliche Schutzwirkung der beiden Sonnencremes zurückzuführen sind und nicht auf unterschiedliche Hauttypen.

Ein balancierter unvollständiger Versuchsplan kann erzeugt werden mit der Funktion design.bib aus dem R-Paket agricolae. Dort anzugeben sind die Anzahl der Behandlungen (v = 3 Sonnencremes) und die Blockgröße (k = 2 Hände). Der genaue Befehl hierfür lautet design.bib ( trt = 1:3 , k = 2 , seed = 42 ). In der unten tabellierten Versuchsplanung wird in jedem Block oben die Behandlung der linken und unten die der rechten Hand aufgelistet. Beachten Sie hierbei, dass der Versuchsplan zufällig konstruiert wird und daher von der Saat Ihres Zufallszahlengenerators abhängt.

Block	Behandlung
1	2
1	3
2	1
2	2
3	3
3	1

Es werden b = 3 Blöcke und damit 3 Probanden benötigt, um einen balancierten unvollständigen Versuchsplan zu erhalten.

Die verwendeten Parameter der statistischen Versuchsplanung werden in der folgenden Tabelle festgehalten:

v	Anzahl an Behandlungen
b	Anzahl an Blöcken
r	Anzahl an Blöcken, welche eine bestimmte Behandlung beinhalten
k	Anzahl an Behandlungen in einem Block
λ	Anzahl an Blöcken, welche zwei bestimmte Behandlungen beinhalten

Die beiden Parameter v = 3 und k = 2 waren vom Versuchsleiter vorgegeben. Die restlichen drei Parameter werden von der Software dazu passend gewählt. 2 Blöcke (2 und 3) beinhalten die Behandlung 1 und entsprechendes gilt auch für die Behandlungen 2 und 3. Von daher ist r = 2 (r steht für repeat = Wiederholungen). Nur ein Block (3) enthält gleichzeitig die Behandlungen 1 und 2 und entsprechendes gilt für die Paare (1,3) und (2,3) von Behandlungen. Deshalb ist λ = 1.

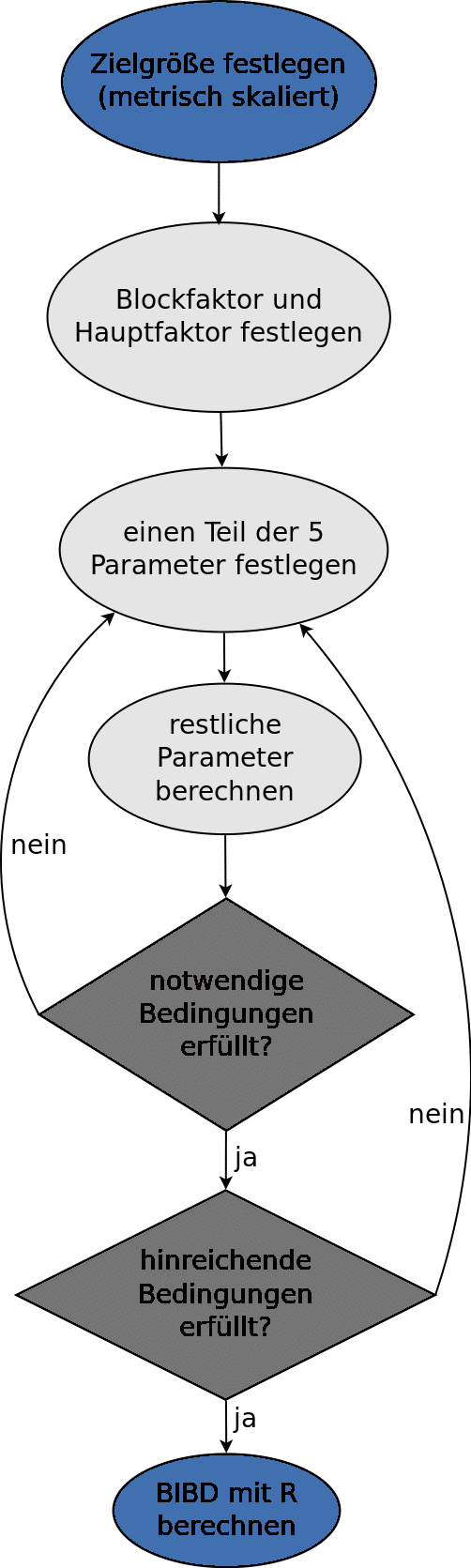
Wann kann ich überhaupt einen balancierten unvollständigen Versuchsplan erstellen?

Ein Versuchsplan gilt als vollständig, falls in jedem Block jede Behandlung mindestens einmal vorkommt. Das ist aus anatomischen Gründen in diesem Beispiel nicht möglich, weil 3 Sonnencremes getestet werden, Menschen aber für gewöhnlich nur 2 Hände besitzen. Beispielsweise fehlt im ersten Block die erste Behandlung. Daher ist dieser Versuchsplan nicht vollständig. Man kann aber auch nicht immer auf einen balancierten unvollständigen Versuchsplan ausweichen. Für die Existenz eines BIBD sind die folgenden drei hinreichenden Bedingungen zu überprüfen:

1. Die Anzahl an Behandlungen ist in jedem Block identisch. (k = 2)
2. Jede Behandlung kommt in der gleichen Anzahl an Blöcken vor. (r = 2)
3. Jedes Paar an Behandlungen kommt in der gleichen Anzahl an Blöcken vor. (λ = 1)

Wenn Sie diese drei hinreichenden Bedingungen und die genannten Parameterwerte (in Klammern) für dieses Beispiel mit der oben tabellierten Versuchsplanung vergleichen, werden Sie feststellen, dass es sich hier tatsächlich um einen balancierten unvollständigen Versuchsplan handelt.

Neben den hinreichenden Bedingungen gibt es auch notwendige Bedingungen für die Existenz eines BIBD:

1. bk = vr
2. λ(v-1) = r(k-1)

Diese notwendigen Bedingungen dienen dazu, geeignete Parameter für einen balancierten, unvollständigen Versuchsplan zu finden. Für die Existenz eines BIBD reicht es nicht aus, die fünf Parameter eines Versuchsplans auf die Einhaltung der notwendigen Bedingungen zu testen. Dafür sind in einem konkreten Versuchsplan die hinreichenden Bedingungen zu überprüfen. Allerdings kann man Parameterkombinationen ausschließen, wenn sie die notwendigen Bedingungen nicht einhalten. Dadurch lassen sich die für ein BIBD in Frage kommenden Parameterkombinationen deutlich beschränken, was bei der Auffindung eines solchen Versuchsplans hilfreich sein kann.

Wie Sie sehen, gibt es also Situationen, in denen kein balancierter unvollständiger Versuchsplan erstellt werden kann. Wenn Sie einen konkreten Versuch planen, wählen Sie deshalb zunächst die Anzahl an Behandlungen insgesamt (v) und die Anzahl an Behandlungen in einem Block (k). Vielleicht haben Sie auch schon eine Vorstellung zur Anzahl der Wiederholungen r einer Behandlung oder der Anzahl an Blöcken b. Die verbliebenen beiden Parameter können Sie dann berechnen, indem Sie das obige Gleichungssystem (notwendige Bedingungen) lösen. Ist dieses nicht lösbar oder ergibt unsinnige Werte, existiert kein BIBD für diese Parameter. Dann sollten Sie die Parameter ändern. Ansonsten können Sie das BIBD gemäß der hinreichenden Bedingungen erstellen, oder die Berechnung einfach Ihrer Statistik-Software überlassen.

So können Sie den Versuchsumfang erhöhen

Die obige statistische Versuchsplanung hat einen sehr kleinen Versuchsumfang mit gerade einmal 2 Wiederholungen einer Behandlung. Denn falls der Parameter r bei der R-Funktion nicht angegeben wird, erstellt die Funktion automatisch eine kleinstmögliche Versuchsplanung mit r = 2. Um die Anzahl jeder einzelnen Behandlung beispielsweise von 2 auf 4 zu verdoppeln, sollten Sie den Parameter r = 4 explizit angeben und erhalten mit dem Befehl design.bib ( trt = 1:3 , k = 2 , r = 4 , seed = 42 ) den Versuchsplan

Block	Behandlung
1	1
1	2
2	3
2	1
3	3
3	2
4	3
4	1
5	2
5	1
6	3
6	2

mit Inzidenzmatrix:

Behandlung	Block 1	Block 2	Block 3	Block 4	Block 5	Block 6
1	1	1	0	1	1	0
2	1	0	1	0	1	1
3	0	1	1	1	0	1

Und so sieht das ganze in R aus:

Statistische Versuchspläne von Novustat

Zu Anfang dieses Artikel haben wir für Sie die Motivation für die Erstellung von statistischen Versuchsplänen begründet. Wir hoffen, dass wir Ihnen mit unserer Expertise in diesem Artikel eine Entscheidungshilfe für die Wahl zwischen einem vollständigen und einem unvollständigen Versuchsplan bieten konnten und Sie unsere Schilderung des Vorgehens zur Erstellung eines balancierten unvollständigen Versuchsplans in R für Ihr eigenes Projekt nutzen können. Wichtig ist jedoch zu beachten, dass dies nur ein Schritt auf dem Weg zu einem professionellen Forschungsplan ist. Wenn Sie Unterstützungsbedarf bei Ihrer Forschungskonzeption haben, kontaktieren Sie uns gern. Novustat unterstützt Sie individuell und kurzfristig bei der Erstellung Ihrer statistischen Versuchsplanung.

Weiterführende Links

[1] https://www.uni-ulm.de/fileadmin/_migrated/content_uploads/DOI_01.pdf

[2] https://de.wikipedia.org/wiki/Statistische_Versuchsplanung