Was ist ein Quantil und wie lässt sich ein Quantil berechnen? – Mit Quantilen lassen sich viele Sachverhalte allgemein verständlich ausdrücken. Etwa im Bereich der Einkommensstatistik. Eine Aussage wie „Ab einem Einkommen von x gehören Beschäftigte zum reichsten Viertel, ab y zum reichsten Zehnten und ab einem Einkommen von z zum reichsten Hundertstel“ ist anschaulich und auch für Laien verständlich.
Zudem ist Quantile berechnen sehr einfach umzusetzen und zugleich sehr aussagekräftig. Streng genommen ist übrigens auch der Median ein Quantil, oft ist vom 50 % Quantil oder 0,5 Quantil die Rede.
Nehmen Sie auch gerne unsere professionelle Statistik Beratung in Anspruch und lassen Sie sich von uns kompetent unterstützen.
Dieser Beitrag erklärt die Aussagekraft von Quantilen und gibt Tipps für die Anwendung. Insbesondere geht es um diese Fragen:
- Was ist ein Quantil?
- Wie kann ich Quantile für die Auswertung nutzen?
- Wie kann ich Quantile in Excel berechnen?
- Welche Formeln verwendet Excel zum Quantile berechnen?
Quantile berechnen: Zunächst eine Definition
Quantile geben Auskunft über die Verteilung eines vom Anwender definierten Bereichs der Stichprobe. In anderen Worten: Quantile sind also Werte, unterhalb oder oberhalb derer ein festgelegter Prozentsatz an Fällen liegt. Bekanntestes Quantil ist der Median, unter und über dem jeweils 50 Prozent der Fälle liegen. Er wird deshalb manchmal auch als 50 % Quantil oder 0,5 Quantil bezeichnet. Weitere bekannte Quantile sind:
| Name | Teilt in … Gruppen |
| Terzil | 3 |
| Quartil | 4 |
| Quintil | 5 |
| Dezil | 10 |
| Perzentil | 100 |
Die Begriffe Quantil (mit n) und Quartil (mit r) werden häufig verwechselt, zumal es auch für beide eine Formel in Excel gibt. Quantile ist allerdings der Überbegriff, Quartile sind eine bestimmte Form von Quantilen. Das unterste Quartil zeigt an, unter welchem Wert 25 Prozent der Fälle liegen, über dem oberen Quartil liegen ebenfalls 25 Prozent. Das mittlere Quartil ist der Median.
Quartile sind noch in einem anderen Zusammenhang wichtig. Der Abstand zwischen dem ersten und dem dritten Quartil, der sogenannte Interquartilsabstand, ersetzt die Standardabweichung als Streuungsmass, wenn dieses nicht berechnet werden kann.
Was ist ein Quantil? – Ein Beispiel
Stellen wir uns ein Unternehmen mit 13 Beschäftigten vor. Wir möchten nun die Quartile für das Alter berechnen.
Diese sind hier nach dem Alter sortiert. Für eine Berechnung in Excel müssen wir die Daten nicht sortieren, es erleichtert aber das Verständnis. In Spalte A steht hier der Name, in Spalte B das Alter.
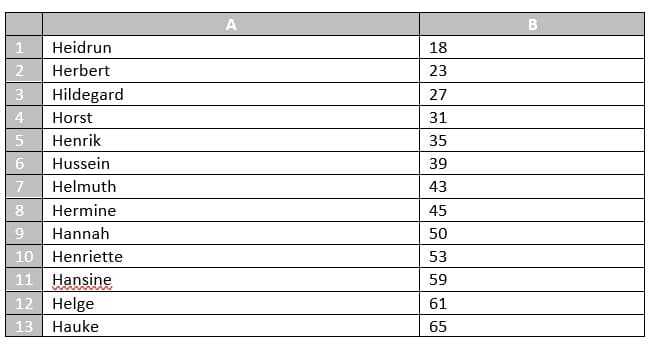
Wer unterhalb des ersten Quartils liegt, gehört zu den jüngsten 25 Prozent, wer über dem dritten liegt, zu den ältesten 25 Prozent. Das zweite Quartil ist zugleich der Median, also jener Wert, zu dem es genauso viele grössere wie kleinere Werte gibt, in unserem Fall also genauso viele ältere wie jüngere Beschäftigte.
Das Schöne an dieser Betrachtung ist nicht nur, dass sie so leicht verständlich ist, sondern dass wir sie auch anstellen können, wenn wir beispielsweise für Hauke und Helge keine genaue Altersangabe hätten, sondern nur die Information „älter als 60“.
Quantile in Excel: die Standardformel
Die Berechnung von Quantilen ist in Excel oder anderen Programmen für die Tabellenkalkulation leicht möglich. Doch aufgepasst, es gibt zwei verschiedene Formeln, die zu unterschiedlichen Ergebnissen kommen, nämlich
- QUANTIL.INKL(;) und
- QUANTIL.EXKL(;).
Diese Unterscheidung gibt es nicht nur in Excel, sondern auch in OpenOffice und LibreOffice. Die richtige Formel nach der gängigen Quantil-Definition ist die obere Formel mit dem Zusatz .inkl. Sie entspricht auch der alten Formel QUANTIL, die bis Excel 2007 verwendet wurde. Mit ihr lassen sich Aussagen treffen wie „25 Prozent der Befragten gaben ein Alter unter … Jahren an“.
Schritt für Schritt Berechnung nach der gängigen Quantil-Definition
Um damit die Quartile auszurechnen, müssen wir in der Klammer vor dem Strichpunkt zunächst den Datenbereich eintragen. In unserem obigen Beispiel wäre das der Bereich B1 bis B13, also =QUANTIL.INKL(B1:B13;…).
Hinter dem Strichpunkt steht die Information, welches Quantil wir suchen. Dafür schreiben wir einen Bruch, er gibt an, welches von wie vielen Quantilen wir suchen, wobei der Maximalwert hier als oberstes Quantil mitgezählt wird.
Für das unterste Quartil schreiben wir deshalb 1/4. Die 1 gibt an, dass wir das erste Quartil suchen, die 4 steht für Quartile, weil diese unsere Gruppe in vier Gruppen einteilen und es einschliesslich des Maximums vier verschiedene Werte gibt.
Wir schreiben also =QUANTIL.INKL(B1:B13;1/4).
Für das zweite Quartil schreiben wir analog dazu 2/4, für das dritte 3/4. Mit 4/4 würden wir den höchsten Wert erhalten, in unserem Beispiel 65. Statt 4/4 können wir auch einfach 1 schreiben, also =QUANTIL.INKL(B1:B13;1) oder die Formel =MAX verwenden. Schreiben wir eine 0, erhalten wir den kleinsten Wert, in unserm Fall die 18. Dies gelingt auch mit der Formel =MIN.
In unserem Beispiel erhalten wir als 1. Quartil das Alter von 31, als Median die 43 und als 3. Quartil die 53.

Wie wir aus der Tabelle ablesen können, liegen unter unserem 1. Quartil 3 Werte, darüber 9, also tatsächlich dreimal so viele. Bei dieser Betrachtung werden auch die übrigen Quartile mitgerechnet, sie sind also inkludiert, daher der Formelzusatz .inkl.
Wir können jetzt auch den Interquartilsabstand berechnen. Da unser 1. Quartil 31 beträgt, das 3. 53, ist der Interquartilsabstand 53 – 31 und damit 22. Dieser Wert wird analog zur Standardabweichung oft als Streuungsmass verwendet.
Sonderfälle: Median und Quartile in Excel
Für den Median, das 50 % Quantil, gibt es eine eigene Formel, sie lautet einfach =Median(). Hier muss in der Klammer lediglich der Datenbereich eingetragen werden.
Weil Quartile neben dem 50 % Quantil das am häufigsten verwendete Quantil in Excel sind, gibt es dafür eine eigene Formel. Sie lautet =QUARTILE.INKL(;), wobei es auch hier analog eine Formel =QUARTILE.EXKL(;) gibt. Auch hier gilt aber, dass die Formel mit dem Zusatz .INKL für die gängige Quantil-Definition die Richtige ist.
Wichtig ist, dass bei dieser Formel nicht nur das N in QUANTIL durch ein R ersetzt wird, sondern dass hier auch die Pluralform verwendet wird, also QUARTILE(;).
Vor dem Strichpunkt steht auch hier der Datenbereich. Weil die Art des Quantils hier bereits definiert ist, muss ich hinter dem Strichpunkt nur angeben, welches Quartil ich suche. Für das unterste Quartil schreibe ich deshalb nicht 1/4, sondern lediglich 1.
Die Formel lautet für unser Beispiel also QUARTILE.INKL(B1:B13;1).
Analog steht für den Median eine 2 und für das dritte Quartil eine 3. Bei 0 wird mir auch hier das Minimum angegeben, bei 4 das Maximum.
Welche Formel verwendet Excel?
Welche Formel verwendet Excel für die Berechnung? Die Hilfe gibt darüber keine Auskunft, allerdings lässt es sich einfach und schnell mit etwas Austesten herausfinden. Der Berechnung liegt folgende Formel zugrunde:
Quantil x = 1 + (Fallzahl – 1) * Nummer des Quartils / Zahl der Gruppen der Quantilsart
In unserem Beispiel gibt es 13 Beschäftigte, die Fallzahl ist also 13. Wir suchen das erste Quartil und Quartile teilen die Gesamtheit in vier Gruppen.
Unsere Formel lautet also:
1. Quartil = (13-1) * 1/4 + 1
13 – 1 ergibt bekanntlich 12. Wir multiplizieren 12 mit ¼ und kommen auf 3. Zum Schluss addieren wir 1 und erhalten als Ergebnis 4.
Das Ergebnis lautet also:
1. Quartil = 1 + 12 ∗ 1/4 = 1 + 3 = 4.
Die Zahl gibt allerdings nur die Position(!) des Quartils wieder, wir müssen also in unserer Liste den vierten Wert suchen. Das ist die 31, so wie es auch Excel berechnet hat.
Analog lautet die Formel für das 3 Quartil:
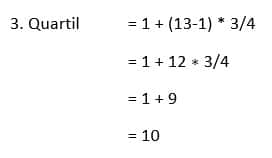
Der 10. Wert ist laut unserer Tabelle die 53, deshalb ist das 3. Quartil 53.
Fazit: Quantile berechnen
In Excel gibt es also zwei verschiedene Formeln für Quantile und Quartile. Üblicherweise wollen wir Aussagen treffen wie: „Nur 1 Prozent der befragten erzielte ein Einkommen von mehr als …. Euro“. Nach dieser Quantil-Definition benötigten wir die Formel =QUANTIL.INKL(;).
In der Klammer müssen wir zunächst den Datenbereich angeben und nach dem Strichpunkt einen Bruch, in dem im Zähler das gesuchte Quartil steht, im Nenner die Zahl der Gruppen, in die das Quantil teilt, etwa 1/5 für das erste Quintil. Für Quartile können wir auch die Formel =QUARTILE.INKL(;) verwenden. Dann steht hinter dem Strichpunkt kein Bruch, sondern nur die Nummer des Quartils, also 1 für das erste Quartil.
Warum es in Excel nun auch noch eine zweite Formel zur Berechnung gibt, um Quantile zu berechnen und was es mit der Formel =QUANTIL.EXKL(;) auf sich hat, erfahren Sie im Blogbeitrag Excel Quantil mit zwei Formeln. Auch durch eine Excel VBA Programmierung lassen sich Quantile berechnen.
Und wenn Sie dazu noch Fragen haben oder Unterstützung für eine Analyse in Excel benötigen, nutzen Sie gerne unser Formular für eine unverbindliche Kontaktanfrage!