Egal ob man Vögel beobachtet, biologische Zelltypen überwacht, oder die Antworten einer Umfrage erfasst – in all diesen Fällen geht es um Variablen, die gezählt werden müssen. Die statistische Analyse solcher sogenannten Zähldaten erfordert spezielle Techniken. Diese Verfahren möchten wir in diesem Artikel gerne vorstellen. In der Statistik sind Zähldaten (auch Zählvariable genannt) ein bestimmter Datentyp, bei welchem Beobachtungen nur nicht-negativen ganzzahlige Werte {0, 1, 2, 3, …} annehmen können und bei denen diese Ganzzahlen eher durch Zählen als durch Rangfolge entstehen. Beispiele für Zähldaten sind z.B. wie viele Unfälle es im vergangenen Jahr in einer Stadt gab oder wie viele Menschen zu einer bestimmten Zeit in einem Einkaufsladen sind. Viele dieser Variablen folgen einer sogenannten Poisson-Verteilung. Für die Analyse solcher Daten für unsere Kunden verwenden wir die sogenannte Poisson-Regression. Ob solch eine Analyse für Ihr Projekt die richtige ist, können Sie auch zügig mithilfe unserer Experten klären.
Dieser Artikel beantwortet folgende Fragen:
- Was sind Beispiele für die Poisson-Verteilung?
- Wie lassen sich Zufallsvariablen der Poisson-Verteilung modellieren?
- Was ist die Poisson-Regression?
Einführung
Für vielfältige Anwendungen der Statistik wird die Methode der linearen Regression genutzt. Immer wenn jedoch Zähldaten zu modellieren sind, ist es empfehlenswert, die verwandte Methode der Poisson-Regression einzusetzen. Denn Zähldaten kann man viel einfacher über eine diskrete Wahrscheinlichkeitsverteilung wie der Poisson-Verteilung modellieren.
Poisson-Verteilung Beispiel:
Für diese Beispiele könnte man eine Poisson-Regression anwenden:
- Die Anzahl der durch Maultier- oder Pferdetreffer getöteten Personen in der preussischen Armee pro Jahr. Dies ist ein klassisches Beispiel für die Poisson-Regression.
- Die Anzahl der Leute, die sich vor dir im Supermarkt anstellen
- Die Anzahl der Auszeichnungen, die Schüler an einer Schule erhalten haben.
- Anzahl der Klicks für eine Webseite pro Tag, die sich durch Online-Werbung ergeben.
Poisson-Regression in der Praxis
Im Folgenden werden wir die Poisson-Regression anhand eines Beispiels kennenlernen. In diesem Poisson-Verteilung Beispiel wollen wir Schülerleistungen anhand von Lernaufwand und Nachhilfe vorhersagen. Als statistische Software wird R eingesetzt.
Daten importieren
Zunächst wollen wir Daten importieren und eine deskriptive Datenauswertung durchführen. Die folgenden Schritte sind zunächst notwendig, um die Daten für die Poisson-Regression vorzubereiten.
dataset <- warpbreaks
names(dataset)=c("Mathepunkte", "Lernen", "Nachhilfe")
levels(dataset$Lernen)[levels(dataset$Lernen)=="A"]="Viel"
levels(dataset$Lernen)[levels(dataset$Lernen)=="B"]="Nichts"
levels(dataset$Nachhilfe)[levels(dataset$Nachhilfe)=="L"]="10h/Woche"
levels(dataset$Nachhilfe)[levels(dataset$Nachhilfe)=="M"]="5h/Woche"
levels(dataset$Nachhilfe)[levels(dataset$Nachhilfe)=="H"]="Keine"
Der Datensatz ist nun importiert und kann betrachtet werden (zum Beispiel mit Rstudio).
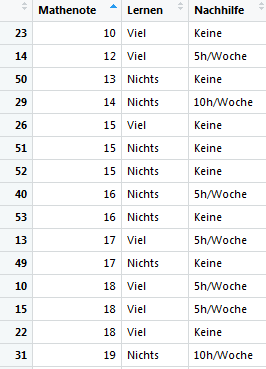
Der Datensatz besteht also aus Schülern, die in einer Mathearbeit eine bestimmte Anzahl an Punkten erreicht haben. Die Anzahl der Punkte sind hier unsere Zähldaten, welche einer Poisson-Verteilung folgen. Die rechten beiden Spalten stellen dar, welchen Lernaufwand die Schüler betrieben haben bzw. ob Nachhilfe in Anspruch genommen wurde. „Lernen“ und „Nachhilfe“ sind hierbei Faktorvariablen.
Deskriptive Analyse
Beginnen wir nun mit der Datenanalyse mithilfe des summary Befehls!
summary(dataset)
Mathepunkte Lernen Nachhilfe
Min. :10.00 Viel :27 5h/Woche :18
1st Qu.:18.25 Nichts:27 10h/Woche:18
Median :26.00 Keine :18
Mean :28.15
3rd Qu.:34.00
Max. :70.00
Wir sehen im Output des summary Befehls, dass minimal 10 Mathepunkte und maximal 70 Mathepunkte erreicht wurden. Mittelwert und Median liegen bei 26 bzw. 28,15. Eine Übersicht über gängige Lageparameter findet sich hier.
Nun wollen wir erst einmal sehen, wie sich die Mathepunkte innerhalb der verschiedenen Levels von „Lernen“ und „Nachhilfe“ unterscheiden.
with(dataset, tapply(Mathepunkte, Lernen, function(x) {
sprintf("M (SD) = %1.2f (%1.2f)", mean(x), sd(x))
}))
Viel Nichts
"M (SD) = 31.04 (15.85)" "M (SD) = 25.26 (9.30)"
Wir sehen also, dass die Schüler, die Viel lernen, im Mittel 31 Punkte bekamen, und die Schüler, die Nichts lernen, 25.26 Punkte. Soweit erscheinen die Ergebnisse sinnvoll.
with(dataset, tapply(Mathepunkte, Nachhilfe, function(x) {
sprintf("M (SD) = %1.2f (%1.2f)", mean(x), sd(x))
}))
5h/Woche 10h/Woche Keine
"M (SD) = 26.39 (9.12)" "M (SD) = 36.39 (16.45)" "M (SD) = 21.67 (8.35)"
Hier sehen wir, dass die Schüler, die viel Nachhilfe bekamen, wiederum am besten abschneiden (36,39 Punkte).
Poisson-Regression
Wir möchten nun die Regression durchzuführen. Das Modell, für das wir uns interessieren, ist
Mathenote =a* Lernen + b*Nachhilfe + Fehler
Wie man sehen kann, ist die abhängige Variable auf der linken Seite der Regressionsgleichung hier eine Zählvariable (Mathenote), daher nutzen wir die Poisson-Regression. Das funktioniert wie folgt.
summary(m1 <- glm(Mathenote ~ Lernen + Nachhilfe, family="poisson", data=dataset))
Der entscheidende Teil ist hierbei
glm(Mathenote ~ Lernen + Nachhilfe, family="poisson", data=dataset)
Call:
glm(formula = Mathenote ~ Lernen + Nachhilfe, family = "poisson",
data = dataset)
Die Ausgabe beginnt mit der Wiederholung des Funktionsaufrufs.
Deviance Residuals:
Min 1Q Median 3Q Max
-3.6871 -1.6503 -0.4269 1.1902 4.2616
Als Nächstes werden die Informationen zu den Residuen angezeigt. Diese Residuen sind bei korrekter Angabe des Modells annähernd normalverteilt und zeigen in unserem Beispiel ein wenig Abweichung hiervon, da der Median nicht ganz Null ist, sondern -0.42.
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.37064 0.05139 65.593 < 2e-16 ***
LernenNichts -0.20599 0.05157 -3.994 6.49e-05 ***
Nachhilfe10h/Woche 0.32132 0.06027 5.332 9.73e-08 ***
NachhilfeKeine -0.19717 0.06833 -2.885 0.00391 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Als Nächstes werden die Poisson-Regressionskoeffizienten für jede der Variablen angezeigt. Ausserdem sind die Standardfehler, z-Scores, p-Werte und 95 % Konfidenzintervalle für die Koeffizienten zu sehen. Die interessantesten Werte sind hier die Koeffizienten. Der Koeffizient für „Nichts-Lernen“ ist beispielsweise -0.20599. Die Interpretation dieser Koeffizienten ist in der Poisson-Regression nicht so einfach wie in der linearen Regression. Um diesen Wert interpretieren zu können, muss diese Zahl zunächst als Exponent der e-Funktion transformiert werden:
e-0.20599= 0.8187
Die Analyse zeigt, dass die Note bei Nichts-Lernen um den Faktor 0.8187 schlechter ist, als wenn dieser Schüler gelernt hätte. Dies ergibt intuitiv Sinn. Zum Beispiel hätte ein Schüler, der gelernt hat und 10 Punkte erreicht hat, ohne zu Lernen nur etwa 8 Punkte erreicht. Falls Sie Hilfe bei der Interpretation ihrer eigenen Outputs benötigen, können wir Ihnen jederzeit helfen.
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 297.37 on 53 degrees of freedom
Residual deviance: 210.39 on 50 degrees of freedom
AIC: 493.06
Number of Fisher Scoring iterations: 4
Die übrigen Angaben dienen der Messung der Anpassungsgüte, also wie gut das berechnete Modell mit den Daten vereinbar ist. Weitere Informationen hierzu finden sich z.B. hier.
Schlusswort
In diesem Blogpost wurde an einem recht einfachen Beispiel gezeigt, wie Poisson-Regression in der Praxis funktioniert und was es für Beispiele für Poisson-Verteilung gibt. Wir wenden diesen immer dann an, wenn Zähldaten modelliert werden sollen, da diese recht häufig einer Poisson-Verteilung folgen. Die Interpretation der Koeffizienten ist nicht so einfach wie bei der linearen Regression.
Die oben beschriebene Variante zeigt nur die grundlegendste Herangehensweise – Zähldaten lassen sich auch mittels anderer Methoden modellieren, die in manchen Anwendungsfällen mehr Sinn machen, beispielsweise wenn viele Nullen in den Zähldaten vorhanden sind oder es ganz bestimmte Häufungswerte gibt. Falls Sie Hilfe bei der Auswahl und Durchführung Ihrer eigenen statistischen Analyse benötigen, stehen unsere Experten Ihnen gerne beratend zur Seite.
