Die Varianzanalyse (oder ANalysis Of VAriance: ANOVA) gehört zu den bekanntesten und meist verwendeten statistischen Verfahren. Ihre Vorteile liegen klar auf der Hand: einfache Berechnung und intuitive Interpretation. Allerdings gibt es für die Varianzanalyse auch Voraussetzungen: die wichtigste ist die Unabhängigkeit der untersuchten Werte. Eine Verletzung dieser Annahme kann zu einer gravierenden Fehlinterpretation der Ergebnisse führen. Im Fall von abhängigen Stichproben, zum Beispiel eben bei Messwiederholungen, gibt es spezifische und genau für solche Designs vorgesehene Anwendungen. Dieser Beitrag gibt eine Einführung in die Varianzanalyse mit Messwiederholung und zeigt ein Beispiel, wie dies mit ANOVA SPSS einfach umgesetzt werden kann.
Sie möchten eine ANOVA mit Messwiederholung durchführen und benötigen dabei Hilfe? – Wenden sie sich hierzu an uns für eine professionelle Beratung!
Varianzanalyse: Grundidee der ANOVA
Wie der Name es bereits vermuten lässt, geht es bei der Varianzanalyse um die Betrachtung der Varianz einer Variablen, konkret einer metrischen Variablen, denn nur solche haben eine Varianz. Zur Erinnerung: die Varianz ist die (oft gemittelte) Summe der quadratischen Abweichung der einzelnen Messwerte von ihrem Gesamtmittelwert. Sie gehört als zentraler Streuungsparameter mit zu den einer der wichtigsten Grössen in der Statistik.
Was macht die Varianz aber so bedeutend? – Hinter dieser Frage steckt die Idee, dass ohne zusätzliches Wissen der Mittelwert einer normalverteilten metrischen Variablen ihr allerbester Schätzwert ist. Für eine Prognose bedeutet das: der Mittelwert ist hierbei die aussagekräftigste Grösse. Die Abweichungen der Stichprobenwerte von dieser Prognose bilden somit die Fehler dieser Schätzung ab. Somit ist Varianz nichts anderes als der Ausdruck eines Gesamtschätzfehlers.
Die Varianzanalyse und damit verwandte Methoden (wie z.B. die Methode der kleinsten Quadrate) versuchen diesen Gesamtfehler zu minimieren, also Schätzwerte zu liefern, die eine kleinere Abweichung von den Messwerten haben als der Gesamtmittelwert. Das erfolgt durch das Hinzufügen neuer Informationen. Un das bildet auch den Kern der ANOVA: Stichproben in Gruppen aufteilen und die Mittelwerte dieser Gruppen als Schätzer nutzen anstelle des Gesamtmittelwerts.
Varianzanalyse für abhängige Stichproben
Bleiben wir aber beim Design ANOVA mit Messwiederholung. Hier liegen folglich mehrere Messungen pro Person vor, die mit einem zeitlichen Abstand vorgenommen werden. In diesem Zeitfenster hat entweder eine konkrete Intervention (Treatment, etc.) stattgefunden oder es haben sich Parameter verändert, die eine Wirkung auf die Messwerte ausgübt haben. Somit haben wir bereits zwei Informationen, die wir unserer Schätzung hinzufügen können: Wir wissen bei jedem Messwert, um welche Person und um welchen Zeitpunkt es sich handelt. Wir haben somit abhängige Stichproben vor uns.
Daran anschliessend folgt eine sogenannte Varianzzerlegung. Die Gesamtvarianz ergibt sich aus der Abweichung der Messwerte aller Personen zu allen Zeitpunkten vom Gesamtmittelwert. Diese Gesamtvarianz lässt sich in einzelne Komponenten zerlegen:
SStotal= SSzwischen_Personen + SSEffekt +SSresidual
Die Varianz zwischen den Personen ist der Teil der Varianz, der auf Unterschiede der untersuchten Personen zurückgeht bzw. dadurch erklärt wird. Wir ignorieren nachfolgend diesen Teil der Varianz. Uns interessiert nämlich, was innerhalb der Personen passiert, sprich: welcher Teil des Fehlers durch die Kenntnis des Messzeitpunktes (=Effekt) reduziert wurde. Der Teil der Varianz, der keiner der beiden Informationen zugewiesen werden kann, ist der verbleibende nicht erklärte Fehler (=Residual).
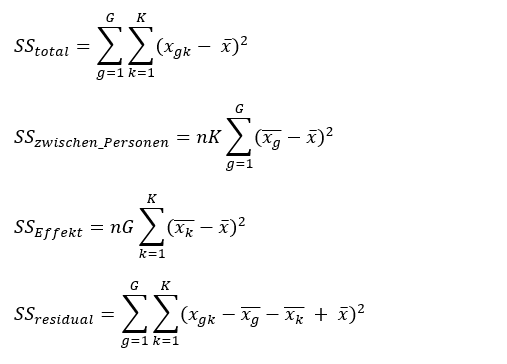
Die Vermengung der Elemente Person und Zeitpunkt ist für abhängige Stichproben bei der Berechnung des Residualfehlers berücksichtigt. Im Weiteren wird die durch die Messzeitpunkte erklärte Varianz näher betrachtet.
Sie benötigen Hilfe bei der Durchführung einer Analyse mit ANOVA SPSS? – Nähere Infos erhalten Sie auch bei unsere Experten in der SPSS-Hilfe!
ANOVA mit Messwiederholung: Einfache Anwendung mit SPSS
ANOVA SPSS bietet eine einfache Möglichkeit, ein Design mit Messwiederholung rechnerisch umzusetzen. Wir demonstrieren das anhand eines Beispiels. Wir nehmen an, 450 Personen wurden einer zweistufigen Behandlung unterzogen. Entsprechend liegen für jede Person jeweils drei Messwerte vor: ein Messwert vor der Untersuchung und jeweils ein weiterer Messwert nach den beiden Behandlungen (Intervention). Im Datensatz sind die drei Messwerte als Variablen jeweils einer Personenzeile zugeordnet.
Auf der SPSS-Schaltfläche wählen wir: „Analysieren“ –> „Allgemeines lineares Modell“ –> „Messwiederholung“
Im erscheinenden Fenster geben wir unserer Untersuchung einen Namen (hier zB.: „Untersuchung“) und benennen die Anzahl der Interventionen bzw. der Messwiederholungen (hier: “3”).
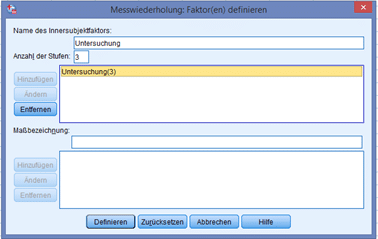
Danach klicken wir auf „Definieren“ und es erscheint folgendes Fenster:
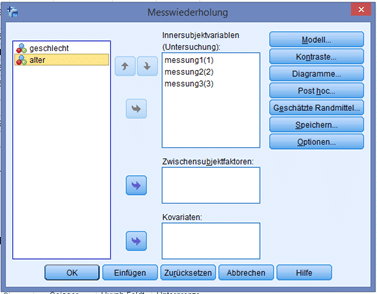
Hier wählen wir unsere drei Variablen (hier „messung1“, „messung2“ und „messung3“), die unsere Messwerte beinhalten, und geben diese in das obere Kästchen zu Intersubjektvariablen. Bei „Optionen“ klicken wir zusätzlich auf die „Schätzung der Effektgrösse“. Damit ist alles für unsere Analyse getan.
SPSS bietet in dieser Umgebung noch weitere Spezifikationen an: in dem mittleren Kästchen können sogenannte Zwischensubjektfaktoren definiert werden, also Gruppen, in die untersuchte Personen zusätzlich eingeteilt werden sollen. Das ist notwendig, falls wir davon ausgehen, dass eine entsprechende Gruppenzugehörigkeit sich auf das Ergebnis auswirkt. In diesem Design (Mixed ANOVA) werden sowohl Variationen zwischen den Subjekten (Personen) als auch innerhalb der Subjekte berechnet. Bei Kovariaten können zusätzlich metrische Kovariablen gewählt werden, wobei meist die Kovarianz zwischen der Kovariaten und der abhängigen Variable herangezogen wird.
ANOVA SPSS: Output und Interpretation
Haben wir das Modell nun definiert und auf „OK“ gedrückt, erscheint das Ergebnis im Ausgabenfenster. SPSS hat die Eigenart, zu jedem Befehl eine Vielzahl an Einzelberechnungen auszuführen und darzustellen. Für unsere Analyse konzentrieren wir uns auf den nachfolgend relevanten Ausschnitt des Outputs:
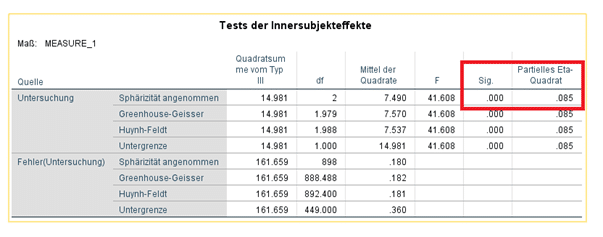
Wir gehen davon aus, dass die Modellannahmen erfüllt sind und betrachten daher nur die oberste Zeile. Das Signifikanzniveau des angewandten F-Tests zeigt an, dass die Messzeitpunkte einen Teil der Gesamtvarianz erklären. Konkret sind es 8,5%, wie das deskriptive Mass Eta-Quadrat anzeigt. Ob diese 8,5% letztendlich als ausreichend bzw. aussagekräftig interpretiert werden, hängt unter anderem von unserer theoretischen Erwartung ab. Ergänzend empfiehlt es sich, deskriptiv die Mittelwerte der einzelnen Messzeitpunkte zu analysieren, um zu wissen, in welche Richtung der Effekt tatsächlich geht. Der Wert der Signifikanz mit .000 belegt zudem den (hoch)signifikanten Einfluss der Messwiederholungen auf die Probanden.
Fazit
Die ANOVA mit Messwiederholung mit einigen wenigen Kontrollvariablen nimmt somit eine Mittelstellung ein zwischen einfachem Mittelwertvergleich mittels t-Test für abhängige Stichproben und komplexen Verfahren wie dem Random Effekt Modell, mit deren Hilfe sich auch nicht lineare Einflüsse oder komplexe Moderations- oder Mediationsbeziehungen besser modellieren lassen. Vor allem bei Experimenten mit relativ kleinen Fallzahlen bietet sich die Varianzanalyse als einfach zu nutzende und aussagekräftige Analysemethode an. Und ANOVA SPSS dient dabei als intuitiv anwendbares Umsetzungstool. Bei weiteren konkreten Fragen kontaktieren Sie uns unverbindlich über das Anfrageformular!