Das Skalenniveau ist sofort in aller Munde, sobald man auch nur vage an die Auswertung statistischer Daten denkt. Warum das so ist und warum das genauso sein muss, erfahren Sie hier. Die Skalenniveaus von Variablen entscheiden darüber, welche Rechenoperationen zulässig sind. In den Niveaus der Skalen der Variablen liegt also die Grundentscheidung darüber verborgen, welche statistischen Testverfahren zur Anwendung kommen können – und dürfen. Die Skalen geben quasi Preis, wie viele Informationen eine Variable bereithält. Ein Beispiel soll hier helfen, das genauer zu erklären.
Wenn Sie Unterstützung bei der Planung Ihrer Studie oder der statistischen Auswertung Ihrer Daten benötigen, sollten Sie sich an die erfahrenen Experten von Novustat wenden. Unsere Statistiker helfen Ihnen weiter mit einer individuellen und bedarfsgerechten Beratung!
Skalenniveaus in der Statistik: Ein Beispiel
Wir stellen die Hypothese auf, dass es einen Zusammenhang zwischen dem Geschlecht einer Person und Ihrer Körpergrösse gibt. Diese Hypothese ergibt sich eventuell aus Ihrer Beobachtung während Sie im Café sitzend einen Kaffee trinken und Ihnen dabei auffällt, dass die Männer, die an Ihrem Tisch vorbeigehen, annähernd alle grösser sind, als die Frauen, die den Weg passieren. Zugegeben, dieser Zusammenhang wurde bereits mehrfach untersucht, stellt jedoch in vielen Statistikübungen noch immer eine gern genommene Berechnung zu Übungszwecken dar.
Sie benötigen Hilfe im Bereich Statistik? Von der Statistik Nachhilfe über die Planung von Studien bis hin zur kompletten Statistik Auswertung – unsere Experten haben umfassende Kenntnisse und helfen Ihnen mit einer massgeschneiderten Statistik Beratung schnell und kompetent weiter!
Skalenniveaus: Sie legen fest, was, wie gerechnet werden darf
Den Sachverhalt des vermuteten Zusammenhangs zwischen Geschlecht und Körpergrösse kann man auf unterschiedliche Arten berechnen. SPSS liefert da eine Fülle an Möglichkeiten, sich der Forschungshypothese zu nähern, die da lautet: Es gibt einen Zusammenhang zwischen dem Geschlecht einer Person und der Körpergrösse. Die der gegenüberstehenden Nullhypothese muss hier lauten: Es gibt keinen Zusammenhang zwischen dem Geschlecht einer Person und Ihrer Körpergrösse. So weit, so gut. Statistisch geprüft haben wir noch nichts, aber Sie erfahren jetzt sofort, warum die Skalenniveaus eine so wichtige Rolle spielen und warum ohne sie eben wirklich nichts geht. Die zu testende Hypothese ist eine ungerichtete Zusammenhangshypothese und fragt danach, ob es einen Zusammenhang gibt – und wie stark derselbe ist. SPSS kennt nun verschiedene Zusammenhangsmasse. Auswählen könnten Sie beispielsweise:
- Chi-Quadrat
- Cramers V
- Kendalls Tau
- Gamma
- Pearsons r und
- den Determinationskoeffizienten.
Alle Zusammenhangsmasse berechnen die statistischen Zusammenhänge auf unterschiedliche Arten und nicht jede Berechnungsart kann für jede Variable angewendet werden. Um hier aus dem Portfolio aller Zusammenhangsmasse das richtige Mass auszuwählen, müssen die Variablen in Bezug auf ihr Skalenniveau klassifiziert werden. Das Skalenniveau einer Variable entscheidet darüber, welche Berechnungen Sie in SPSS durchführen lassen können, um die Hypothese zu überprüfen. Dies gilt natürlich auch für die Auswahl egal welcher Rechenoperation – und auch dann, wenn Sie Berechnungen aus Übungszwecken per Hand durchführen wollen – oder müssen.
Das Skalenniveau gibt Auskunft darüber, wie viele Informationen eine Variable bereithält, wie komplex die Rechenoperationen sein dürfen und können, die Sie für die Variable und das statistische Testen auswählen.
Sie haben die Qual der Wahl: drei Skalenniveaus wollen unterschieden werden
Die drei Skalenniveaus können als eine Hierarchie betrachtet werden. Auf der untersten Stufe steht dabei das nominale Skalenniveau. Danach folgt das ordinale Skalenniveau. Auf der obersten Stufe steht schliesslich das metrische Skalenniveau.
Die unterste Stufe: Das nominale Skalenniveau
Das erste Skalenniveau der Hierarchie, welches auch den geringsten Informationsgehalt hat und am wenigsten Rechenoperationen ermöglicht, ist das nominale Skalenniveau. Ein Beispiel dafür ist die Ihnen bereits bekannte Beispielvariable Geschlecht. Für Variablen der Nominalskala lassen sich immer Entscheidungen über Gleichheit oder Ungleichheit treffen. Wenn Sie an Ihren Datensatz denken, auf dessen Grundlage Sie etwas statistisch testen möchten, ist andere Variablen mit einer Nominalskala beispielsweise der Geburtsort – weitere Beispiele sind folgende:
- Zugehörigkeit zu einer Abteilung (Mitarbeiterbefragung)
- die Religionszugehörigkeit,
- die Art des Haustieres,
- das Lieblingsessen,
- Urlaubsziele usw.
Hier kann immer die Entscheidung darüber getroffen werden, ob eine Aussage zutrifft oder nicht. Abstufungen zwischen den Ausprägungen sind nicht möglich, man kann keine Abstände messen, es gibt keinen Nullpunkt und man kann keine Hierarchie bilden. Das sind Merkmale, anhand derer man erkennen kann, dass es sich um eine Nominalskala handelt.
Diese Charakterisierungen treffen auch auf die Beispielvariable Geschlecht zu. Nominalskalen haben keine nummerisch messbaren Eigenschaften. Man kann zwar aus Berechnungsgründen Codes für die Ausprägungen „männlich“ und „weiblich“ vergeben, zahlenmässig erheben kann man Variablen mit nominalem Skalenniveau nicht.
Die oberste Stufe: Das metrische Skalenniveau
Das Gegenteil zum nominalen Niveau liefert die zweite Beispielvariable: die Körpergrösse. Diese Variable hat ein metrisches Skalenniveau. Warum? Darum: Metrische Skalen haben von allen drei Skalenniveaus den höchsten Informationsgehalt und ermöglichen die meisten und damit auch komplexestes Rechenoperationen. Die Körpergrösse eines Menschen kann erhoben werden in Zentimetern. Hier ist es also möglich, Abstände zwischen den einzelnen Ausprägungen zu berechnen und es können klare Hierarchisierungen erfasst werden. Eine Körpergrösse von 180 cm ist deutlich grösser als eine von 150 cm. Ausserdem gibt es einen natürlichen Nullpunkt, der für die Interpretation nicht immer grossen Sinn macht, aber es gibt ihn.
Andere metrisch skalierte Variablen sind zum Beispiel: das Alter in Jahren, das Einkommen in Euro, die Wohnungsgrösse in Quadratmetern. Aber auch Variablen, die nach Einstellungen und Meinungen fragen, sind metrisch skaliert.
Die Zwischenstufe: Das ordinale Skalenniveau
Gelesen haben Sie nun von zwei Skalenniveaus – vom ersten, dem einfachsten, und vom dritten, dem komplexesten Skalenniveau. Eins fehlt noch, es liegt genau dazwischen und nennt sich ordinales Skalenniveau. Beispiele für dieses Skalenniveau sind:
- der Schulabschluss,
- Gehaltsgruppen,
- Rangfolgen,
- aber auch kategorisierte Variablen, die beispielsweise metrisch skalierte Variablen zusammenfassen.
Variablen mit ordinalem Skalenniveau bieten mehr Informationsgehalt als nominale Variablen, aber weniger als solche mit metrischem Skalenniveau. So kann zum Beispiel eine Hierarchisierung vorgenommen werden, eine Berechnung der Abstände ist jedoch nicht möglich.
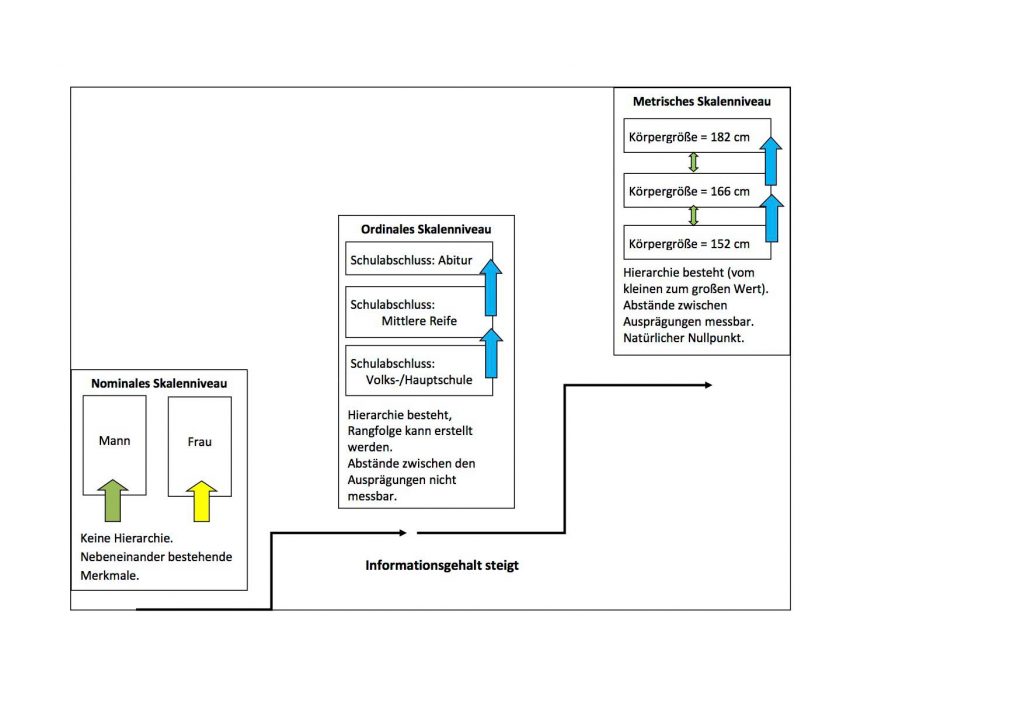
Das Skalenniveau als Hierarchie dargestellt
Vor der Auswertung: Das Skalenniveau SPSS mitteilen
Damit Sie für jede Variable das richtige Skalenniveau identifizieren können, braucht es ganz am Anfang zwar etwas Übung, aber mit Hilfe der kleinen Beispiele haben Sie mit Sicherheit schnell die Übung, um Ordnung in die Niveaus zu bringen. Bevor Sie also die Entscheidung für eine Rechenoperation fällen können, schauen Sie sich zuerst die betreffenden Variablen an und fragen Sie sich, welche Niveaus sie wohl haben. Bedenken Sie bitte stets, dass das Skalenniveau auch dann von Ihnen zu identifizieren ist, wenn Sie die Berechnung mit Hilfe von SPSS durchführen. Für eine Variable Ihrer Wahl gilt: um für die Ermittlung vom Skalenniveau SPSS anzupassen, müssen Sie die Variablenansicht des Datensatzes aufrufen und dort für die Variable von den drei vorgegebenen Möglichkeiten (nominal, ordinal, metrisch) die passende Variante auswählen. Sie müssen das richtige Skalenniveau SPSS quasi mitteilen, da sonst für alle Variablen in der Regel „Skala“, also das metrische Skalenniveau, voreingestellt ist.
Eine kleine Zusammenfassung zum Schluss
Bevor Sie also die Datenauswertung mittels SPSS beginnen, müssen Sie die Niveaus Ihrer Skalen identifizieren. Und nun zum Schluss: Im Falle unserer Hypothese kann jetzt die Entscheidung gefällt werden. Der Zusammenhang kann mit Hilfe eines Zusammenhangsmasses für nominale Skalenniveaus getestet werden. Warum? Weil wir uns bei unterschiedlich skalierten Variablen an das Motto halten müssen: das schwächste Glied gibt den Ton an. Und das ist in diesem Falle die Variable Geschlecht mit dem geringsten Skalenniveau (nominal), da hilft uns leider die metrische Skala der Körpergrösse nichts. Hier sind beispielsweise Chi-Quadrat und Cramers V die Masse der Wahl und darüber kann die Stärke des Zusammenhangs der beiden Variablen getestet werden. Probieren Sie das Ganz für Ihren Datensatz doch mal aus.