In der medizinischen Forschung werden häufig mehrere Hypothesen innerhalb einer Studie geprüft, etwa bei verschiedenen Fragestellungen oder Subgruppen. Dieses multiple Testen erhöht das Risiko, zufällig signifikante Ergebnisse zu erhalten. Die Folge ist eine sogenannte Alphafehler-Kumulierung, bei der die Gesamtwahrscheinlichkeit für einen Fehler 1. Art steigt. Klassische Verfahren wie die Bonferroni-Korrektur setzen genau dort an, bleiben aber oft konservativ und schränken die Teststärke ein. Eine Einführung in die Grundlagen der Alphafehler-Kumulierung und Bonferroni-Korrektur finden Sie in diesem Artikel zum multiplen Testen.
Ein alternativer Ansatz sind hierarchische Testverfahren, bei denen Hypothesen in einer festgelegten Reihenfolge geprüft werden. In diesem Beitrag erfahren Sie, wie diese Verfahren funktionieren, welche Varianten es gibt und wie sie am Beispiel medizinischer Studien angewendet werden.
Hierarchische Teststrategien im Überblick
In der medizinischen Forschung ist es üblich, im Rahmen einer Studie mehrere Hypothesen gleichzeitig zu prüfen. Das betrifft nicht nur verschiedene Patientengruppen oder Zeitpunkte, sondern häufig auch mehrere sogenannte Endpunkte. Damit sind messbare Zielgrössen gemeint, anhand derer beurteilt wird, ob eine Therapie wirksam oder sicher ist. Beispiele sind etwa die Überlebensdauer, die Reduktion von Symptomen oder bestimmte Laborparameter.
Wenn Forschende mehrere Hypothesen gleichzeitig testen, steigt das Risiko einer Alphafehler-Kumulierung. Klassische Korrekturverfahren wie die Bonferroni-Methode behandeln alle Hypothesentests gleichwertig und reduzieren das Signifikanzniveau entsprechend. Dadurch sinkt jedoch die Teststärke, insbesondere wenn viele Tests durchgeführt werden.
Hierarchische Verfahren bieten eine alternative Strategie zur Kontrolle der Alphafehler-Kumulierung. Dabei wird nicht davon ausgegangen, dass alle Hypothesen gleichrangig und gleichzeitig zu prüfen sind. Stattdessen erfolgt die Testung in einer vordefinierten Reihenfolge, etwa basierend auf zeitlicher Abfolge oder der Relevant für die Studienfrage. Die Signifikanzprüfung verläuft schrittweise: Nur wenn der erste Test ein signifikantes Ergebnis liefert (also die zugehörige Nullhypothese verworfen wird), wird die nächste Hypothese geprüft. Diese Vorgehensweise spiegelt häufig auch die inhaltliche Logik klinischer Studien wider. So kann beispielsweise die Wirksamkeit einer Behandlung als erste Priorität gelten, bevor Fragen zur Lebensqualität oder zu biologischen Mechanismen untersucht werden.
Ein Vorteil hierarchischer Teststrategien liegt darin, dass sie das gesamte Signifikanzniveau effizient nutzen können, ohne es auf alle Tests gleichmässig aufteilen zu müssen. Dadurch bleibt mehr statistische Power erhalten; vorausgesetzt, die Reihenfolge der Hypothesen ist gut begründet und wird vorab festgelegt.
Planung klinischer Studien mit hierarchischen Tests
Damit ein hierarchisches Testverfahren korrekt zum Einsatz kommt, legen Forschende die Reihenfolge der Hypothesentests bereits vor Studienbeginn fest, typischerweise im Studienprotokoll und im Statistischen Analyseplan (SAP).
Dabei wird häufig zwischen primären, sekundären und gelegentlich auch explorativen Endpunkten unterschieden:
- Der primäre Endpunkt ist die wichtigste Zielgrösse der Studie. Er dient häufig als Grundlage für die Fallzahlberechnung und spielt eine zentrale Rolle bei Zulassungsentscheidungen. Ein typisches Beispiel ist die Wirksamkeit einer Therapie, etwa gemessen an der Überlebenszeit oder an der Reduktion klinischer Symptome.
- Sekundäre Endpunkte liefern ergänzende Informationen, zum Beispiel zur Lebensqualität der Patienten oder zur Veränderung bestimmter biologischer Marker (z. B. Entzündungswerte).
- Explorative Endpunkte dienen häufig der Hypothesengenerierung und werden meist nicht formal inferenzstatistisch interpretiert.
Hierarchische Testverfahren ermöglichen es, diese Endpunkte einer Studie entsprechend ihrer inhaltlichen Relevanz zu priorisieren und in eine prüfbare Reihenfolge zu bringen. Die Grundidee lautet: Forschende testen die Hypothesen nicht gleichzeitig, sondern in einer zuvor festgelegten Abfolge. Dadurch lässt sich das Signifikanzniveau effizient kontrollieren, ohne unnötig an Teststärke zu verlieren.
Eine solche Priorisierung ergibt sich oft direkt aus der zuvor beschriebenen Einteilung in primäre, sekundäre und explorative Endpunkte. In einer medizinischen Studie könnte dies beispielsweise so aussehen:
- Verlängerung der Überlebenszeit
- Verbesserung der Lebensqualität
- Veränderung eines Biomarkers (z. B. Entzündungswerte)
Diese Priorisierung bildet häufig die Grundlage für die spätere statistische Teststrategie. Für jeden dieser Endpunkte wird in der Regel eine statistische Hypothese formuliert, die anschliessend im Rahmen der Auswertung geprüft wird. Wie genau dieser Testprozess ablaufen kann, zeigen wir anhand zweier verbreiteter Methoden im nächsten Abschnitt: dem Fixed-Sequence-Verfahren und dem Gatekeeping-Verfahren.
Fixed-Sequence-Verfahren
Das Fixed-Sequence-Verfahren ist die einfachste Form eines hierarchischen Testverfahrens. Es folgt einer festen Reihenfolge von Hypothesentests, die Forschende streng nacheinander prüfen. Sie verwenden das gesamte Signifikanzniveau (z. B. α = 0,05) jeweils für den aktuellen Test. Erst wenn ein Test signifikant ausfällt, gehen sie zur nächsten Hypothese über.
Diese Methode ist besonders gut geeignet, wenn die Hypothesen logisch oder klinisch klar priorisiert sind.
Beispiel: Medikamentenstudie mit drei Hypothesen
Eine klinische Studie untersucht ein neues Medikament zur Behandlung einer chronischen Erkrankung. Es werden drei Hypothesen getestet:
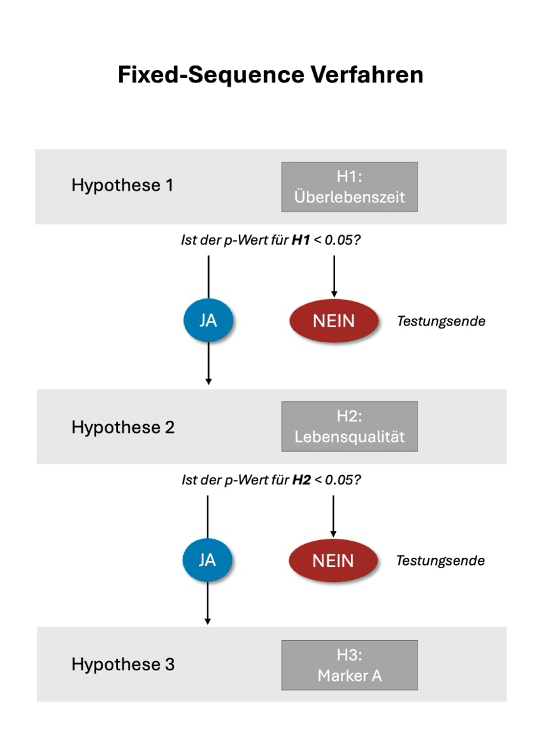
- H1: Das Medikament verlängert die durchschnittliche Überlebenszeit.
- H2: Das Medikament verbessert die subjektiv erlebte Lebensqualität.
- H3: Das Medikament reduziert einen Entzündungswert (Marker A).
Der Ablauf dieses Verfahrens lässt sich anschaulich in folgender Grafik nachvollziehen:
Gatekeeping-Verfahren
Das Gatekeeping-Verfahren ist eine Erweiterung des Fixed-Sequence-Prinzips. Forschende setzen das Gatekeeping-Verfahren ein, wenn sie in einer Studie mehrere Hypothesengruppen prüfen, die sich inhaltlich oder formal voneinander abgrenzen lassen, zum Beispiel primäre Wirksamkeitsziele und nachgelagerte explorative Analysen. Solche Gruppen werden im statistischen Kontext als families of hypotheses (Hypothesenfamilien) bezeichnet.
Eine Familie besteht aus mehreren Hypothesen, die thematisch oder funktional zusammengehören und gemeinsam einem Korrekturverfahren unterzogen werden. Das Gatekeeping-Verfahren regelt, unter welchen Bedingungen eine nachgeordnete Familie überhaupt getestet werden darf. Damit lassen sich auch komplexe Studiendesigns strukturieren, ohne auf übermässig konservative Korrekturen zurückgreifen zu müssen.
Beispiel: Medikamentenstudie mit zwei Hypothesenfamilien
Eine Studie zu einem neuen Medikament definiert folgende Hypothesengruppen:
- Familie A (Wirksamkeit)
- H1: Verlängerung der Überlebenszeit
- H2: Verbesserung der Lebensqualität
- Familie B (Biomarker)
- H3: Veränderung eines Entzündungswerts (Marker A)
- H4: Veränderung eines genetischen Expressionswerts (Marker B)
Die Teststrategie folgt dem Gatekeeping-Prinzip: Forschende prüfen zunächst Familie A. Nur wenn diese die festgelegten Signifikanzkriterien erfüllt, testen sie anschliessend Familie B. Innerhalb jeder Familie kann ein geeignetes Korrekturverfahren wie Bonferroni, Holm oder Hochberg eingesetzt werden, um die Fehlerwahrscheinlichkeit über mehrere Hypothesentests hinweg zu kontrollieren.
Ob alle Hypothesen in einer Familie signifikant sein müssen (serielles Gatekeeping), bereits einzelne ausreichen (paralleles Gatekeeping) oder eine komplexe Pfadstruktur entsteht (baumartig strukturiertes Gatekeeping), hängt vom Studiendesign ab.
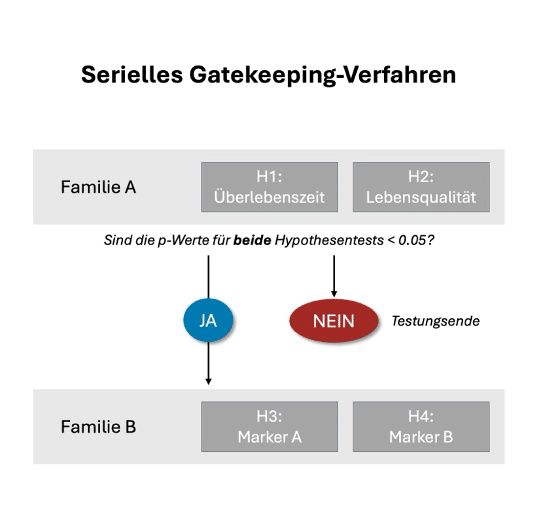
Serielles Gatekeeping
Beim seriellen Gatekeeping prüfen Forschende die nächste Hypothesenfamilie nur dann, wenn alle Hypothesen der vorherigen Familie signifikante Ergebnisse zeigen. Diese Variante gilt als besonders streng und kommt häufig in zulassungsrelevanten Studien zum Einsatz.
Paralleles Gatekeeping
In dieser Variante reicht es aus, wenn mindestens eine der Hypothesen einer Familie signifikant sind, um weitere Familien zu testen. Das Signifikanzniveau kann anteilig weitergegeben werden, beispielsweise über einen sogenannten Rejection Gain Factor.

Baumartige Gatekeeping-Strukturen (tree-structured)
In komplexeren Studiendesigns können die Hypothesengruppen verzweigt angeordnet sein. Welche nachgelagerten Hypothesenfamilien Forschende testen, hängt davon ab, welche Hypothesen in einer übergeordneten Ebene signifikante Ergebnisse liefern. So entstehen differenzierte Testpfade, z. B.:
– Wenn H1 signifikant → teste H3 und H4
– Wenn H2 signifikant → teste nur H5
– Wenn H3 und H4 signifikant → teste H6
– Wenn H5 signifikant → teste H7 und H6

Vor- und Nachteile hierarchischer Verfahren zur Kontrolle der Alphafehler-Kumulierung
Hierarchische Teststrategien wie das Fixed-Sequence- oder Gatekeeping-Verfahren bieten gegenüber klassischen Korrekturmethoden wie der Bonferroni-Korrektur eine Reihe von Vorteilen, insbesondere dann, wenn Hypothesen logisch priorisiert oder in Gruppen zusammengefasst werden können.
Hierarchische Verfahren nutzen das Signifikanzniveau besonders effizient: Da sie es nicht pauschal auf alle Tests aufteilen, erhalten Forschende mehr Teststärke für die jeweils geprüften Hypothesen. Gleichzeitig ermöglichen sie eine inhaltlich strukturierte Auswertung, was gerade in klinischen Studien mit primären und sekundären Endpunkten entscheidend sein kann.
Allerdings erfordern hierarchische Verfahren auch eine sorgfältige Planung. Forschende müssen die Reihenfolge oder Gruppierung der Hypothesen im Vorfeld klar festlegen und dürfen sie nachträglich nicht verändern. Zudem schränken bestimmte Testpfade die Auswertung stark ein: Wenn eine frühe Hypothese keinen signifikanten Befund liefert, berücksichtigen die Verfahren alle nachfolgenden Hypothesen nicht – selbst wenn deren p-Werte unter 0,05 liegen.
Die folgende Übersicht zeigt verschiedene Strategien zur Kontrolle der Alphafehler-Kumulierung beim multiplen Testen.
| Verfahren | Vorgehen | Vorteile | Einschränkungen | Geeignet für … |
| Bonferroni-Korrektur | Gleichzeitige Tests, Alpha durch Anzahl der Tests geteilt | Einfach, konservativ, leicht anwendbar | Geringe Teststärke bei vielen Hypothesen | Explorative Analysen, viele gleichrangige Tests |
| Fixed Sequence | Hypothesentests in fester Reihenfolge | Maximale Teststärke, transparent, regulatorisch anerkannt | Kein Test der Folge-Hypothesen bei fehlender Signifikanz | Klare Priorisierung einzelner Hypothesen |
| Gatekeeping | Hypothesenfamilien mit festgelegter Prüfstruktur | Flexibel, erlaubt Gruppenbildung, realitätsnah | Aufwändig in Planung und Dokumentation | Komplexe Studien mit mehreren Endpunkten |
Praktische Umsetzung in der Studienpraxis
Damit Sie hierarchische Verfahren korrekt angewenden, sind einige praktische Voraussetzungen und Planungsschritte zu beachten. Die folgenden Punkte helfen dabei, typische Fehler zu vermeiden und die statistische Gültigkeit zu sichern.
- Dokumentation im Studienprotokoll und SAP
- Legen Sie die Reihenfolge oder Gruppierung der Hypothesen bereits vor Studienbeginn fest und dokumentieren Sie diese schriftlich im Studienprotokoll sowie im Statistischen Analyseplan (SAP).
- Vermeiden Sie Änderungen nach Beginn der Datenerhebung, denn sie gefährden die Gültigkeit der Analyse und werden von Zulassungsbehörden in der Regel nicht akzeptiert.
- Kombination mit Korrekturverfahren
- Setzen Sie innerhalb von Gruppen (z. B. bei einem Gatekeeping-Ansatz) klassische Korrekturverfahren wie Holm oder Bonferroni ein, um mehrere gleichrangige Hypothesen statistisch abzusichern.
- Auch adaptive Varianten (z. B. Fallback-Strategien, Recycling-Alpha) sind möglich, erfordern aber meist höhere methodische Expertise.
- Regulatorische Anforderungen
- Behörden wie die EMA (European Medicines Agency, EU-Arzneimittelbehörde) FDA (Food and Drug Administration, US-Arzneimittelbehörde) erkennen hierarchische Verfahren ausdrücklich an; vorausgesetzt, sie sind transparent geplant und begründet.
- Die Wahl des Verfahrens sollte zur Studienlogik und den Endpunkten passen, insbesondere bei Zulassungsstudien.
Typische Stolperfallen vermeiden
- Nachträgliche Änderung der Hypothesenreihenfolge (z. B. basierend auf ersten Ergebnissen) führt zum Verlust der Kontrolle über das Fehlerniveau.
- Unklare Priorisierung: Fehlt eine klare Priorisierung der Hypothesen und erscheinen diese gleichwertig, empfiehlt es sich, auf ein hierarchisches Verfahren zu verzichten.
- Intransparente Kommunikation im Protokoll erschwert die Nachvollziehbarkeit und kann die Akzeptanz durch Review-Gremien gefährden.
Fazit
Die Kontrolle der Alphafehler-Kumulierung ist ein zentraler Bestandteil jeder wissenschaftlichen Studie mit mehreren Hypothesentests. Während klassische Korrekturverfahren wie die Bonferroni-Methode einfach anzuwenden sind, stossen sie bei komplexen Studiendesigns mit mehreren Zielgrössen schnell an ihre Grenzen.
Hierarchische Verfahren wie das Fixed-Sequence- oder das Gatekeeping-Verfahren bieten in diesen Fällen eine methodisch robuste und regulatorisch anerkannte Alternative. Forschende können damit das Signifikanzniveau effizient nutzen, Hypothesen gezielt priorisieren und die Aussagekraft ihrer Studie absichern – vorausgesetzt, sie planen die Teststrategie im Vorfeld sorgfältig und setzen sie konsequent um.
Auch wenn dieser Beitrag medizinische Studien als Beispiel nutzt, lassen sich hierarchische Testverfahren grundsätzlich auch in anderen wissenschaftlichen Disziplinen anwenden. Wenn Sie in der Studienplanung vor der Herausforderung stehen, multiple Endpunkte oder Hypothesengruppen statistisch sauber abzubilden, unterstützen wir Sie gern – unser Team verfügt über fundierte Erfahrung im Bereich medizinischer Statistik.
Weiterführende Literatur:
Dmitrienko, A., & Tamhane, A. C. (2010). Gatekeeping procedures in clinical trials. In A. Dmitrienko & A. C. Tamhane (Hrsg.), Multiple testing problems in pharmaceutical statistics (S. 165–191). Chapman and Hall/CRC. Verfügbar unter https://web.njit.edu/~wguo/Math654_2012/DTB_Chapter5.pdf
European Medicines Agency. (2002). Guideline on multiplicity issues in clinical trials. Verfügbar unter https://www.ema.europa.eu/en/documents/scientific-guideline/points-consider-multiplicity-issues-clinical-trials_en.pdf
U.S. Food and Drug Administration. (2022). Multiple endpoints in clinical trials: Guidance for industry. Verfügbar unter https://www.fda.gov/regulatory-information/search-fda-guidance-documents/multiple-endpoints-clinical-trials