In Studien werden meist viele Daten gesammelt. Gerade im Umfeld von genetischen Studien in der Medizin oder Biologie werden mit Hilfe der Biometrie tausende Genlokalisationen gleichzeitig untersucht. Oft werden dabei mehr Daten erfasst, als für die Beantwortung der eigentlichen Frage (Primärhypothese) notwendig sind. Oft liegen die Daten ohnehin schon vor. Es könnte ja sein, dass sich noch ein signifikanter Zusammenhang zeigt… Diese Art der statistischen Auswertung wird als multiples Testen bezeichnet. Dabei werden viele statistische Signifikanztests hintereinander durchgeführt. Wird multiples Testen ohne Adjustierung Statistik durchgeführt, dann ist das Vorgehen vergleichbar mit Angeln im Trüben: Irgendwann beisst schon ein Fisch an, man muss nur ausdauernd genug suchen! Um aber valide und interpretierbare Ergebnisse zu erhalten muss eine Adjustierung Statistik vorgenommen werden. Wir zeigen Ihnen deshalb anhand der Bonferroni-Korrektur, wie eine Alpha-Fehler-Kumulierung vermieden werden kann.
Das Testen mehrere Hypothesen ist in der Praxis Alltag. Daher haben wir auch schon für zahlreiche Kunden eine Korrektur für multiples Testen im Rahmen einer Datenauswertung vorgenommen. Unsere Statistik-Beratung unterstützt gerne auch Sie, in welchem Mass multiples Testen in Ihren Daten berücksichtigt werden muss.
Multiples Testen: Worauf muss man aufpassen?
- Welche Verfahren zur Adjustierung Statistik gibt es?
- Wie kann man die Alpha-Fehler-Kumulierung umgehen?
- Was versteht man unter Bonferroni-Korrektur?
- Wie verwendet man eine geeignete Adjustierung Statistik in der Praxis?
Der Fehler beim statistischen Testen
Beim statistischen Testen wird versucht, auf Basis der beobachteten Daten Rückschlüsse auf die Grundgesamtheit zu treffen. Dazu führt man einen statistischen Test durch, um allgemeingültige Aussagen zu treffen. Diese Verallgemeinerung ist allerdings immer mit einer Wahrscheinlichkeit für eine Fehlentscheidung verbunden: Man kennt ja nur einen kleinen, repräsentativen Ausschnitt der Grundgesamtheit.
Angenommen, zwei Gene werden hinsichtlich der Expression miteinander verglichen. Mit einem statistischen Test erhält man einen p-Wert von 0,015. Das bedeutet, die Wahrscheinlichkeit, dass ein solches oder noch extremeres Ergebnis wie in der Stichprobe beobachtet werden kann, obwohl tatsächlich beide Gene die gleiche Expression bewirken, beträgt 1,5 %. Das ist sehr unwahrscheinlich. So unwahrscheinlich, dass man die Nullhypothese ablehnt. Da der p-Wert unter dem Signifikanzniveau von 5 % liegt, spricht man dann von einem signifikanten Testergebnis, die Alternativhypothese gilt als bewiesen.
Multiples Testen
Ergibt der Vergleich der Expression von zwei Genen einen p-Wert von 0,015 ist dies also sehr unwahrscheinlich. Vergleicht man die Expression eines Gens dagegen mit 60 anderen, die sich tatsächlich hinsichtlich der Expression nicht voneinander unterschieden, so spricht ein p-Wert von 0,015 nicht mehr für ein seltenes Ereignis: Mit einer Wahrscheinlichkeit von 1-(1-0,05)Anzahl der Tests = 1-0,9560= 95,4 % zeigt mindestens einer der Tests einen p-Wert unter 5 %. Und das, obwohl tatsächlich kein Unterschied vorhanden ist!
Viele Tests, viele mögliche Fehlerentscheidungen
Mit der Anzahl der durchgeführten Tests steigt also die Wahrscheinlichkeit, eine falsch positive (signifikante) Aussage zu machen – immerhin kann man sich ja bei jedem Test irren. Werden mehrere unabhängige Tests nacheinander durchgeführt, steigt die Wahrscheinlichkeit sehr schnell an, dass mindestens eine Falschaussage gemacht wird. Bei drei Tests und einem Signifikanzniveau von 5 % beträgt die Wahrscheinlichkeit dafür immerhin schon 1-0,953 = 14,3 %:
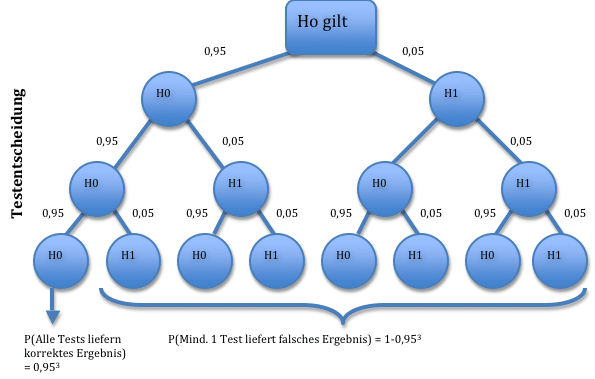
Die Alpha-Fehler-Kumulierung
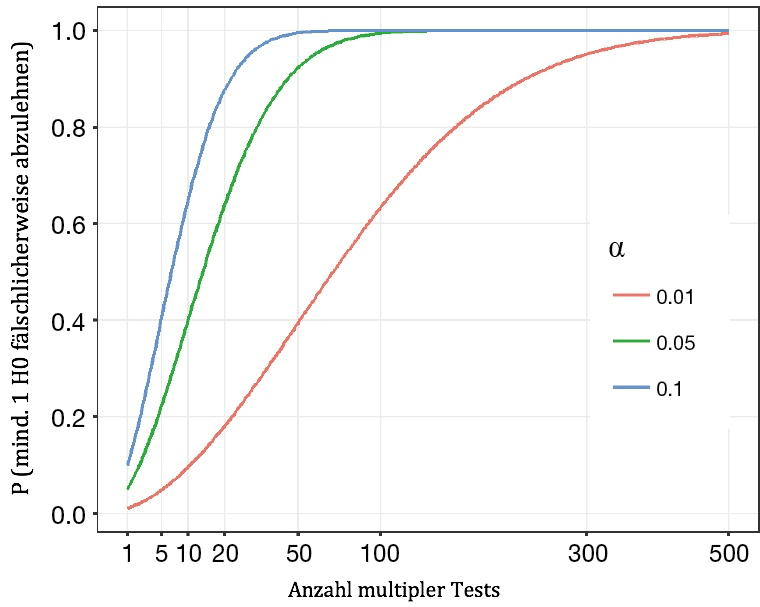
Werden mehrere Hypothesen an demselben Kollektiv gleichzeitig getestet, dann steigt die Wahrscheinlichkeit einer Falschaussage mit der Anzahl der durchgeführten Tests. Dieses Phänomen wird Alpha-Fehler-Kumulierung genannt. Alpha-Fehler-Kumulierung tritt auf, wenn:
- Mehrere Hypothesen mit einem Datensatz überprüft werden.
- Mehrere verschiedene Endpunkte mit statistischen Tests überprüft werden
- Subgruppenanalysen durchgeführt werden
- Verschiedene Einzelergebnisse zu einem Gesamtergebnis zusammengefasst werden
- Interimsanalyse
Adjustierung p-Wert oder Signifikanzniveau
Die Testentscheidung wird getroffen, indem der p-Wert mit dem zu erreichenden Signifikanzniveau Alpha verglichen wird. Somit gibt es zwei Möglichkeiten zur Adjustierung: Anpassung des Signifikanzniveaus oder Berechnung korrigierter p-Werte. Beide Verfahren sind gleichberechtigt, wenn es darum geht der Alpha-Fehler-Kumulierung entgegenzuwirken. Für die Interpretation muss allerdings klar herausgestellt sein, welches Kriterium korrigiert wird. Bei einer Vielzahl komplexer Testverfahren ist eine Korrektur des p-Wertes allerdings nicht einfach umzusetzen. Eine Verringerung des Signifikanzniveaus ist daher meist die einfachere Wahl.
Möglichkeiten zur Adjustierung Statistik
Um der Alpha-Fehler-Kumulierung entgegenzuwirken, und ein globales Signifikanzniveau sicherzustellen, müssen für die einzelnen Testungen striktere Regeln angewendet werden. Das Signifikanzniveau der Einzeltests wird heruntergesetzt, sodass insgesamt das Signifikanzniveau von 5 % eingehalten werden kann.
Hierzu gibt es eine grosse Auswahl an Verfahren. Das restriktivste und zugleich einfachste Verfahren ist dabei die Bonferroni-Korrektur.
Die Bonferroni-Korrektur
Die Bonferroni-Korrektur testet jeden Einzeltest auf einem reduzierten Signifikanzniveau. Das Signifikanzniveau der Einzeltests ergibt sich dabei als global einzuhaltendes Signifikanzniveau dividiert durch die Anzahl der Einzeltests. Werden bei einer Studie 20 einzelne Testungen durchgeführt, für die das globale Signifikanzniveau von 5 % einzuhalten ist, müssen die p-Werte der Einzeltests also unter 0,05/20 = 0,0025 liegen, um als signifikant zu gelten.
Dieses Verfahren dabei hält immer das globale Signifikanzniveau ein und verhindert damit zuverlässig eine Alpha-Fehler-Kumulierung. Allerdings sind die Regeln oft so streng, dass keine signifikanten Ergebnisse mehr übrig bleiben. Es gibt eine ganze Reihe alternativer Methoden, die das Signifikanzniveau besser ausschöpfen: Dazu gehören beispielsweise Benjamini-Hochberg, Holm, Duncan, Student–Newman–Keuls (SNK), Ryan–Einot–Gabriel–Welsch (REGW). Die beste Korrektur hängt dabei sehr stark von den Daten ab. Wir beraten Sie hierzu gerne individuell.
Ein Beispiel aus der Beratungspraxis: Auswertung von genetischen Daten
Das Problem des multiplen Testens rückt mit genetischen Studien vermehrt in den Fokus. In der vorliegenden Studie wurde der genetisch bedingte Einfluss auf die pathologische Komplettremission eines Tumors untersucht. Für jeden der 2000 eingeschlossenen Patienten wurde hierzu ein Genotypensatz mit etwa 500000 Single Nucleotide Polymorphism (SNPs) erstellt. In der genomweiten Assoziationsstudien (GWAS) sollte ein Zusammenhang mit der Tumorremission (ja/nein) untersucht werden.
Zuerst wurden im Rahmen der Qualitätskontrolle alle SNPs mit nur einer Ausprägung ausgeschlossen. Weitere Überprüfungen, insbesondere auf die Erfüllung des Hardy-Weinberg Gleichgewicht reduzierten den Datensatz schliesslich auf 20 relevante SNPs.
Die SNPs wurden als kategoriale Variable mit den Ausprägungen 0, 1 und 2 kodiert.
Die primäre Hypothese wurde dann mit einem logistischen Modell überprüft. Die Ergebnisse sind in der folgenden Tabelle zusammengefasst:
Ergebnisse der logistischen Regression
| SNP | Effekt (ss) | OR (exp(ss)) | p-Wert | Signifikanz unadjustiert | Signifikanz nach Bonferroni-Korrektur | |
| 1 | Tp11115 | -0,114 | 0,892 | 0,020 | * | * |
| 2 | Tp1155 | 0,224 | 1,252 | 0,042 | * | |
| 3 | Tp11555 | -0,971 | 0,379 | <0,001 | * | * |
| 4 | Tp12454 | 0,579 | 1,785 | 0,007 | * | * |
| 5 | Tp1488 | 0,227 | 1,254 | 0,040 | * | |
| 6 | Tp15165 | 0,303 | 1,354 | 0,020 | * | * |
| 7 | Tp15444 | -0,130 | 0,878 | 0,015 | * | |
| 8 | Tp15555 | 0,466 | 1,594 | 0,009 | * | * |
| 9 | Tp15599 | -0,119 | 0,888 | 0,018 | * | |
| 10 | Tp187634 | -0,105 | 0,900 | 0,028 | * | |
| 11 | Tp453104 | 0,640 | 1,897 | 0,001 | * | * |
| 12 | Tp4555 | 0,437 | 1,548 | 0,010 | * | * |
| 13 | Tp4888 | -0,002 | 0,998 | 0,054 | ||
| 14 | Tp4888 | 0,230 | 1,259 | 0,038 | * | |
| 15 | Tp48888 | -0,243 | 0,784 | 0,009 | * | * |
| 16 | Tp48899 | 0,025 | 1,025 | 0,064 | ||
| 17 | Tp6975798 | -0,739 | 0,478 | 0,004 | * | * |
| 18 | Tp764123 | 0,202 | 1,224 | 0,051 | ||
| 19 | Tp87441 | -0,015 | 0,985 | 0,035 | * | |
| 20 | Tp74125 | -0,856 | 0,425 | 0,001 |
Insgesamt zeigen 17 SNPs einen p-Wert unter den Signifikanzniveau α = 5 %. Allerdings wurden insgesamt 20 Variablen getestet, so dass man damit rechnen muss, dass ein bis zwei signifikante p-Werte unter der 5 % Grenze liegen, obwohl in Wahrheit gar kein Effekt vorliegt. Wendet man hingegen die Bonferroni-Korrektur für multiples Testen an, so wird das Signifikanzniveau an die Anzahl der durchgeführten Tests angepasst: Der kritische Wert nach Bonferroni-Korrektur beträgt dann 0,05/20 = 0,0025. Mit dieser strengeren Regel zeigen nur mehr 9 SNPs ein signifikantes Ergebnis. Insgesamt wird so allerdings die Wahrscheinlichkeit für den Fehler 1. Art über alle betrachteten SNPs auf 5 % begrenzt.
Publikation – Berichterstellung
Die Verwendung von Methoden zur Korrektur von multiplen Testen müssen in jedem Bericht erwähnt werden. In prospektiven Studien müssen die Verfahren ausserdem bereits im Studienprotokoll festgelegt werden.
Die Nichtbeachtung führt zu zahlreichen falsch-positiver Ergebnisse, also Signifikanzen, die in der Wirklichkeit gar nicht vorliegen. Insbesondere die Berichterstattung von vornehmlich signifikanten Ergebnissen führt zu einem sogenannten Publikationsbias. Sind falsch-positive Ergebnisse erst einmal publiziert, so dauert es meist lange, bis dieser widerlegt werden können. Zeigen Tests nach der Adjustierung Statistik für multiples Testen keine Signifikanz mehr, so heisst das nicht, dass die Ergebnisse bedeutungslos geworden sind.
Wann kann auf eine Korrektur für multiples Testen verzichtet werden?
Korrektur für Multiples Testen bezieht sich nur auf die Einhaltung der Wahrscheinlichkeit für den Fehler 1. Art. Falsch-positive Ergebnisse werden somit unter Kontrolle gehalten. Sind bei Testungen ohne Adjustierung p-Werte über dem Signifikanzniveau, also nicht signifikante p-Werte, so müssen diese auch nicht korrigiert werden.
Eine Adjustierung Statistik für multiples Testen ist immer notwendig, wenn Schlüsse von der Stichprobe auf die Grundgesamtheit in Form von vielen statistischen Tests gemacht werden. Oft ist es aber gar nicht notwendig, oder sogar sinnvoll, jede Fragestellung mit einem Test anzusichern. Explorative Auswertungen können z.B. sehr detailliert und anschaulich die Stichprobe beschreiben und neue Zusammenhänge aufdecken. Wird dabei kein Rückschluss auf die Grundgesamtheit vorgenommen, so sind keine Tests notwendig und die Notwendigkeit der Adjustierung Statistik entfällt.
Für weitere Vorschläge und eine individuelle statistische Beratung bezüglich der Auswertung stehen Ihnen unsere Experten zur Verfügung.
Zusammenfassung
Es liegt in der Natur des statistischen Testens, dass falsche Schlussfolgerungen möglich sind. Diese Wahrscheinlichkeit steigt dabei mit jedem zusätzlichen p-Wert, der berechnet wird! Die Signifikanzschranken müssen daher an die Anzahl der durchgeführten Tests angepasst werden. Eine Möglichkeit der Adjustierung ist beispielsweise die Bonferroni-Korrektur.
Darüber hinaus gibt es aber noch eine Vielzahl alternativer Korrekturverfahren, die weniger Powerverlust zur Folge haben. Gerne beraten wir sie hierzu individuell, welche Verfahren für Ihre Problemstellung optimal sind. Nehmen Sie Kontakt mit uns auf!
Weiterführende Informationen/Quellen
Ralf Bender, Stefan Lange, Adjusting for multiple testing—when and how?, Journal of Clinical Epidemiology, Volume 54, Issue 4, 2001, Pages 343-349, ISSN 0895-4356
Chen, S. Y., Feng, Z., & Yi, X. (2017). A general introduction to adjustment for multiple comparisons. Journal of thoracic disease, 9(6), 1725–1729. doi:10.21037/jtd.2017.05.34
Victor et al.: Hinweise zum Umgang mit multiplen Testen, Deutsches Ärzteblatt 4/2010, S. 50-56
