Alle statistischen Tests prüfen letztendlich, ob beobachtete Daten für oder gegen eine bestimmte Vorhersage sprechen. Hierzu ist die Berechnung von p-Werten (engl. p-values) unerlässlich. Im folgenden Artikel dreht sich deshalb alles um diese besondere Masszahl der Statistik p-Wert: Berechnen von Wahrscheinlichkeiten unter bestimmten Annahmen. Solche Berechnungen werden in allen Anwendungsbereichen gebraucht – von der statistischen Auswertung eines Fragebogens bis zur klinischen Forschung. Dass die Schritte dahinter kein Hokuspokus sein müssen, wollen wir Ihnen in diesem Blog zeigen.
Wenn Sie Unterstützung bei der Auswertung oder Interpretation Ihrer Daten benötigen, helfen unsere Statistiker Ihnen gerne weiter. Kontaktieren Sie uns für eine kostenlose Beratung & ein unverbindliches Angebot.
Folgende Fragen werden in diesem Artikel beantwortet
- Wie kann man den p-Wert berechnen?
- Wie kann man sinnvoll den p-Wert interpretieren?
- Welchen Zusammenhang gibt es zwischen p-Wert, Signifikanz und statistischem Testproblem?
- Was versteht man unter einem asymptotischen p-Wert (asym. p-value)?
- Wie kann man den p-wert berechnen mit Excel und SPSS?
Vom Zeckenbiss in die Welt der Wahrscheinlichkeitsrechnung: p-Wert Statistik per Hand
Die Firma Pharnix will überprüfen, ob das neu entwickelte Medikament Zwickdinix die Häufigkeit von Zeckenbissen verringern kann. Im Voralpenland werden etwa 30% der Landwirte in einer Saison von einer Zecke gebissen.
Statistisch gesehen handelt es sich dabei um ein klassischen einseitigen Hypothesentest:
H0: Die Wahrscheinlichkeit für einen Zeckenbiss bei Behandlung von Zwickdinix ist gleich 30%.
Vs.
H1: Die Wahrscheinlichkeit für einen Zeckenbiss nach Behandlung mit Zwickdinix ist geringer als 30%.
Die Firma Pharnix möchte nun die Hypothesen untersuchen und den entsprechenden p-Wert berechnen. Dazu wird zunächst eine klinische Studie durchgeführt: 20 Landwirte cremen sich täglich mit Zwickdinix ein. In einem Zeitraum von 9 Monaten wird jeder Zeckenbiss dokumentiert. Insgesamt werden dabei nur 3 Zeckenbisse bei den Landwirten gezählt. Die „Erfolgswahrscheinlichkeit“ ist somit 3/20=0,15. Es wurden tatsächlich weniger Zeckenbisse beobachtet als man ohne das Medikament erwartet hätte. Ist das nun Zufall? Oder ist Zwickdinix tatsächlich ein tolles, wirksames Medikament gegen Zeckenbisse?
Um das zu beantworten, müssen wir ein bisschen in die Statistik eintauchen. Wir müssen zunächst klären, wie wahrscheinlich es ist, dass drei von den insgesamt 20 Bauern von einer Zecke gebissen wurde, wenn die Erfolgswahrscheinlichkeit bei 0,3 liegt.
Wünschen Sie ein massgeschneidertes und individuelles Coaching zum Verständnis und Anwendung statistischer Verfahren? Oder Sie benötigen Hilfe bei der Auswertung und Interpretation Ihrer Daten? Von der Statistik Nachhilfe bis hin zur Unterstützung durch eine vollständige statistische Auswertung: Unsere Experten helfen Ihnen schnell und kompetent weiter!
P-Wert berechnen per Hand: Kein Hexenwerk!
Die Wahrscheinlichkeit lässt sich berechnen mittels der Formel
\(Pr(X=k)=\binom{n}{k}p^k(1-p)^{n-k}\)n gibt die Anzahl der Beobachtungen (Stichprobenumfang) an, hier also n=20. P ist die Erfolgswahrscheinlichkeit der Zecken, also p=0,3 und k ist die beobachtete Anzahl von Zeckenbissen in der Studie, und damit k=3.
Der erste Faktor \(\binom{n}{k}\) gibt die Anzahl der verschiedenen Reihenfolgen an, bei denen ein Zeckenbiss auftauchen kann. Schliesslich ist es ja für die Berechnung egal, ob Landwirt 1, 2,… oder 20 den Zeckenbiss hatte –, auch wenn der jeweilige Bauer das vielleicht etwas anders sieht.
Damit ergibt sich für die Wahrscheinlichkeit, dass k=3 Zeckenbisse bei n=20 Testpersonen mit einer Erfolgswahrscheinlichkeit von p=0,3 auftreten als
\(Pr(X=k)=\binom{n}{k}p^k(1-p)^{n-k}=\binom{20}{3}\cdot 0,3^3\cdot 0,7^{17}=0,07160\)Diese Wahrscheinlichkeit ist also sehr klein. Führt man die identische Studie wiederholt durch, so kommt es in 7,160% der Wiederholungen zu 3 Zeckenbissen bei 20 Beobachtungen, falls das Medikament Zwickdinix unwirksam ist.
In der folgenden Tabelle sind die Wahrscheinlichkeiten für andere Werte von k angegeben:
| k | Pr(X=k) |
| 0 | 0,0008 |
| 1 | 0,0068 |
| 2 | 0,0278 |
| 3 | 0,0716 |
| 4 | 0,1304 |
| 5 | 0,1789 |
| 6 | 0,1916 |
| 7 | 0,1643 |
| 8 | 0,1144 |
| 9 | 0,0654 |
| 10 | 0,0308 |
| 11 | 0,0120 |
| 12 | 0,0039 |
| 13 | 0,0010 |
| 14 | 0,0002 |
| 15 | 3,730E-05 |
| 16 | 5,007E-06 |
| 17 | 5,050E-07 |
| 18 | 3,607E-08 |
| 19 | 1,627E-09 |
| 20 | 1,842E-11 |
Somit erhält man folgendes Histogramm:
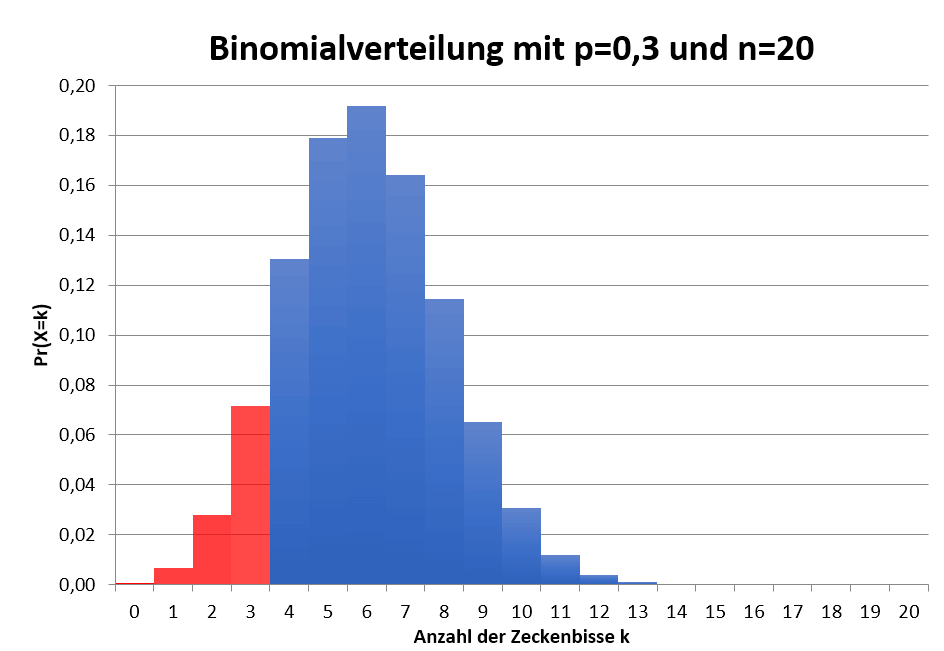
Interpretation des p-Werts
Der p-Wert gibt nun die Wahrscheinlichkeit an, die beobachtete Anzahl an Zeckenbisse oder eine extremere Anzahl zu erhalten unter der Bedingung, dass die Nullhypothese gilt.
Sehr theoretisch, im Histogramm oder obiger Tabelle aber gut zu sehen: Wir haben k=3 beobachtet. Eine bessere oder „extremere“ Wirkung von Zwickdinix hätten wir noch gesehen, falls k kleiner als 3 ist, also 2, 1 oder 0. Wenn wir die p-Wert berechnen möchten können wir dies also anhand obiger Tabelle tun: \(p-Wert = Pr(X\leq k|H0) = 0,07160 + 0,02785 + 0,00684 + 0,00080 = 0,10709\).
Wie Zeckenbisse in Zukunft vermieden werden können: Kleiner p-Wert – grosse Wirkung

Die Firma Pharnix wollte vor allem den p-Wert berechnen um diesen mit dem Signifikanzniveau α zu vergleichen. Ist dieser p-Wert kleiner als das vor Studienbeginn definierte Signifikanzniveau α, so spricht man von einem signifikantem p-Wert. Wenn das Mittel Zwickdinix keinerlei Wirkung hätte, würde man nur mit einer Wahrscheinlichkeit von p=0,10709 weniger als 4 Zeckenbisse bei einem Stichprobenumfang von 20 beobachten. Wird diese Wahrscheinlichkeit kleiner als ein vorher festgelegter Schwellenwert (Signifikanzniveau α), so sieht man das als Indiz dafür, dass die Nullhypothese unwahrscheinlich ist und nicht gilt. Stattdessen kann man von der Alternativhypothese H1 ausgehen. Die Alternative gilt als statistisch nachgewiesen.
Ist der p-Wert höher als das Signifikanzniveau, so lautet das Testergebnis: H0 kann nicht abgelehnt werden. Es ist kein Nachweis für die Alternative erbracht.
Jetzt erst recht: p-Wert berechnen bei hohen Fallzahlen
Dies in Erinnerung überlegt die Firma Pharnix eine neue Studie in Auftrag zu geben, um die Wirksamkeit von Zwickdinix nachzuweisen. Sie beschliesst nach einer Statistik Beratung mit kompetenten Statistikern die Fallzahl deutlich zu erhöhen. So startet im nächsten Jahr nochmals eine Studie mit dem gleichen Studiendesign und einem Stichprobenumfang von 2000 Landwirten. Nach neun Monaten werden 170 Landwirte mit Zeckenbissen beobachtet.
Wenn wir nun die Wahrscheinlichkeit für 170 oder weniger Zeckenbisse berechnen wollen mit einer Binomialverteilung bei einer Fallzahl von 2000 Landwirten ist dies eine abendfüllende Tätigkeit. Die Obige obige Tabelle hätte dann 2001 Zeilen, für den p-Wert müssten wir 171 Wahrscheinlichkeiten addieren. Um die Berechnungen zu vereinfachen, können wir uns zu Nutze machen, dass die Binomialverteilung für grosse Stichprobenumfänge immer glatter wird. Die Verteilung nähert sich einer Normalverteilung an.
Wenn man die Verteilung normiert, so dass die Spitze bei Null liegt (indem man den Mittelwert von allen Beobachtungen abzieht) und die Streuung der Daten in x-Achsenrichtung gleich eins wird (indem man durch die Standardabweichung teilt), so hat man näherungsweise eine Standardnormalverteilung vor sich.
Unter der Annahme, dass die Nullhypothese stimmt, ist die standardisierte Testgrösse standardnormalverteilt. Die Wahrscheinlichkeit Pr(X<170) kann dann aus dem Tabellenwerk der Standardnormalverteilung abgelesen werden. Der resultierende p-Wert wird deshalb auch oft als asymptotischer p-Wert bezeichnet, da er aus Tabellen bestimmt wird, die nur näherungsweise gelten. Die Näherung ist dabei umso besser, je grösser der Stichprobenumfang ist.
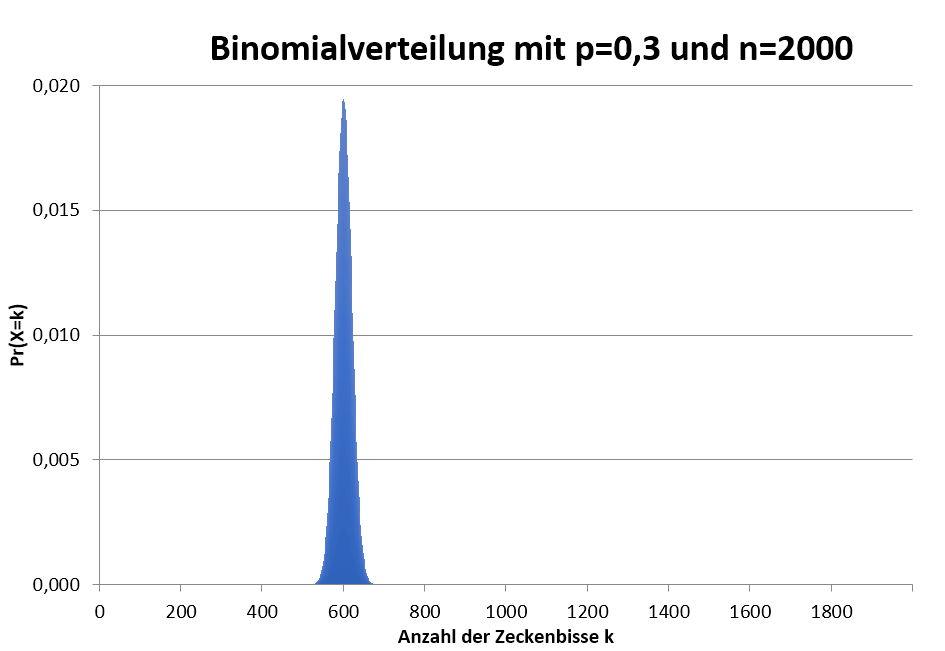
Das Histogramm einer Binomialverteilung mit n=2000 ist bereits sehr glatt, Balken können nicht mehr identifiziert werden.
Konkret berechnet sich der asymptotische p-Wert in folgenden Schritten:
1. Aufstellen der Hypothesen:
H0: p=0,3 d.h. Zwickdinix reduziert die Anzahl der Zeckenbisse nicht
Vs.
H1: p<0,3, Zwickdinix verringert die Anzahl der Zeckenbisse
2. Berechnung der Teststatistik.
Hier asymptotisch, da n=2000; d.h. Subtraktion des Mittelwertes \((n\cdot p)\) und Division durch die Standardabweichung \(\sqrt{(p (1-p)/n)}\)
Berechnung des Mittelwertes:
\(n\cdot p=2000\cdot 0,3=600\)
Berechnung der Standardabweichung:
\(\sqrt{n\cdot p \cdot (1-p)}=\sqrt{2000 \cdot 0,3 \cdot 0,7}=\sqrt{420}=20,49\)
Teststatistik:
\(Z_{obs}=\frac{170-600+0,5}{20,49}=\frac {-429,5}{20,49}=-20,96\)
3. P-Wert berechnen durch Vergleich mit dem Tafelwerk einer Standardnormalverteilung
\(Pr(X<z_{obs}|Ho)=Pr(X<-20,96)= 7,60436\cdot10^{-98} <0,001\)4. Vergleich mit dem Signifikanzniveau α und Testentscheidung.
Da p<0,001<α = 0,05 kann die Nullhypothese abgelehnt werden. Die Alternative wird also angenommen. Der Wirkstoff Zwickdinix hat eine signifikante Verringerung von Zeckenbissen zur Folge.
p-Wert berechnen wie die Profis: IBM SPSS und MS Excel im Einsatz
Nach den guten Erfahrungen in der Studienplanung mit den Statistikern lässt Pharnix die statistische Auswertungen der Studie auch von Profis durchführen. Die Studiendaten werden hierzu am Computer erfasst und die Auswertung mit SPSS durchgeführt. Wie im Studienprotokoll vorgesehen werden die Hypothesen mit dem Binomialtest überprüft. Die folgenden Abbildungen zeigen, wie der Binomialtest in SPSS aufgerufen wird sowie die Ergebnisse des statistischen Tests.
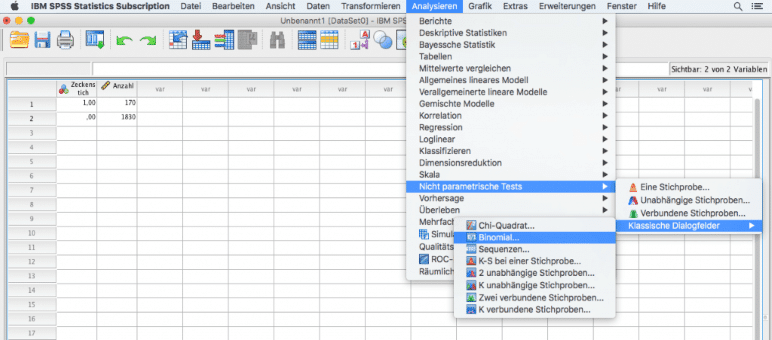
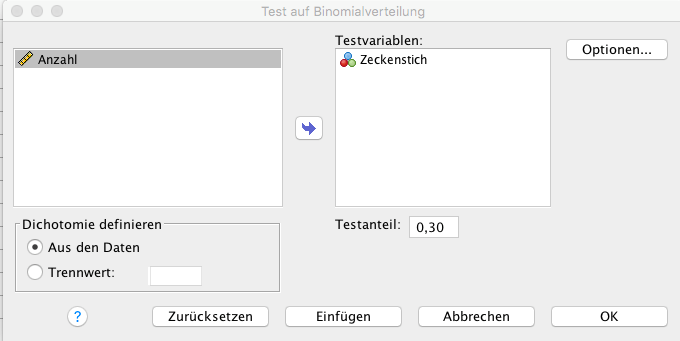
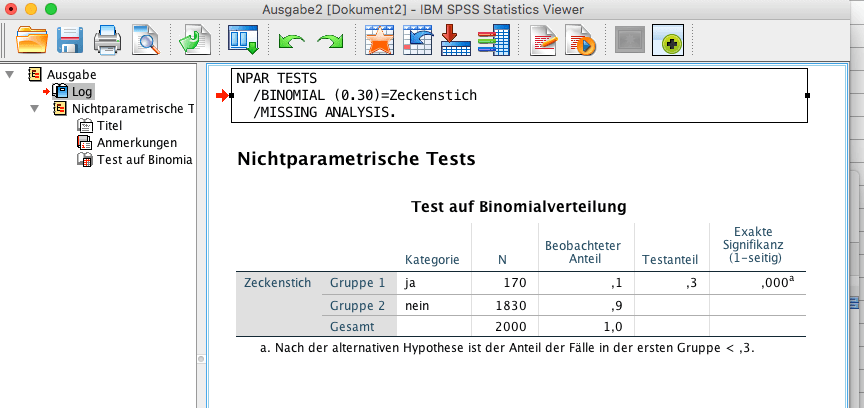
Bei der Berechnung des Binomialtest gibt SPSS tabellarisch eine Zusammenfassung der beiden Gruppen an. Zeckenbisse hatten 170 von 2000 Untersuchungseinheiten, das entspricht einem beobachteten Anteil von 0,1. Der p-Wert wird in SPSS als Signifikanz bezeichnet. Der einseitige Test führt zu einem p-Wert <0,001. Denn P-Werte =0 gibt es nicht! Der Test ist also auf dem Signifikanzniveau von 5% statistisch signifikant: es kann nachgewiesen werden, dass die Creme Zwickdinix wirksam ist.
Auch mit MS Excel können mit entsprechendem Fachwissen p-Werte berechnet werden. Für den Binomialtest steht die Funktion BINOMVERT() zu Verfügung. Als Argumente werden dabei die Zahl der Erfolge, der Stichprobenumfang, die unter Ho zu erwartende Erfolgswahrscheinlichkeit und einen Indikator, damit alle in Richtung Alternative extremere Werte aufaddiert werden. Die entsprechende Formeln für die Zeckenstudie lauten somit =BINOMVERT(3;20;0,3;1) bzw. =BINOMVERT(170;2000;0,3;1).
Zusammenfassung
In diesem Artikel haben wir Ihnen anhand einer klinischen Studie gezeigt, wie man bei einem statistischen Testproblem den p-Wert berechnen kann. Dabei gibt es entscheidende Punkt zu beachten. Angefangen vom richtigen Studiendesign, der Fallzahlplanung (bei zu wenig Beobachtungen kann auch der beste Wirkstoff nicht nachgewiesen werden!), dem Aufstellen der Hypothesen und dem richtigen, leistungsfähigem statistischen Test. All diese Punkte sind entscheidend für eine korrekte p-Wert Signifikanz Aussage.
Experten Tipp: die meisten Funktionen von SPSS lassen sich auch durch eine Excel VBA Programmierung realisieren!
Wir sind für Sie da in allen statistischen Angelegenheiten. Oft lassen sich mit einer professionellen statistischen Beratung teure und zeitraubende Fehler vermeiden.
Weiterführende Quellen:
Fahrmeir L, Heumann C, Künstler R, Pigeot I, Tutz G – Statistik: Der Weg zur Datenanalyse. 8. Auflage.
