Die logistische Regression (auch Logit Modell) ist ein sehr nützliches Verfahren für eine Vielzahl von Anwendungsfällen: So kann eine binäre logistische Regression vorhersagen ob ein Kunde ein Produkt kauft und welche Faktoren diese Entscheidung beeinflussen. Genauso kann eine logistische Regression bestimmen, welche Risikofaktoren das Auftreten einer Erkrankung wahrscheinlicher machen. Aber wann genau macht der Einsatz einer logistischen Regression tatsächlich Sinn? Diese Frage kann bei der Vielzahl an möglichen statistischen Verfahren schnell zur Verwirrung führen. Wir wollen daher mit diesem Artikel deshalb ein wenig Klarheit schaffen: In diesem Artikel wird durch leicht nachvollziehbare Erklärungen und Praxisbeispiele der sinnvolle Einsatz für die (binäre) logistische Regression einfach erklärt! Für unsere Praxisbeispiele werden wir für die logistische Regression SPSS verwenden. Das Logit Modell wird aber natürlich von allen gängigen Statistikprogrammen unterstützt.
Wenn Sie zum Thema logistische Regression Unterstützung wünschen, zögern Sie nicht unsere Statistik Hilfe in Anspruch zu nehmen!
Dieser Artikel beantwortet folgende Fragen:
- Wann sollte ich das Logit Modell verwenden?
- Was ist der Unterschied zwischen einer logistischen Regression und einer linearen Regression?
- Was ist der Unterschied zwischen einem Chi-Quadrat Test und einer logistischen Regression
Logistische Regression SPSS: Warum Regression?
Die logistische Regression gehört wie der Name schon sagt zu der Familie der Regressionsanalysen. Geläufige Arten der Regressionsanalyse sind neben der logistischen Regression beispielsweise auch die lineare Regression. Diese Regressionsanalysen haben dabei eines gemeinsam: Die Regressionsanalyse untersucht den Zusammenhang zwischen einer abhängigen Variable (z.B. Kaufentscheidung: ja/nein) mit einer oder mehreren unabhängigen Variablen (z.B. Alter, Geschlecht, wahrgenommener Nutzen des Produkts, etc.). Damit eignen sich Regressionsanalysen ideal dafür, um Zusammenhänge von Variablen mit einer Zielvariable zu untersuchen. Eine Regressionsanalyse kann aber auch für Vorhersagen genutzt werden (z.B.: Wie wahrscheinlich ist eine Kaufentscheidung für einen männlichen Kunden von 37 Jahren und einem hohen wahrgenommen Nutzen des Produkts?).
Was unterscheidet jetzt aber eine logistische Regression von anderen Arten der Regressionsanalyse? Um das zu verdeutlichen stellen wir im folgenden Teil die logistische Regression der linearen Regression gegenüber. Einen ersten Überblick über die Gemeinsamkeiten und Unterschiede der beiden Verfahren liefert die folgende Tabelle:
| Verfahren | Abhängige Variable | Unabhängige Variable |
|---|---|---|
| Lineare Regression | 1 kontinuierliche Variable | 1+ Variable(n) (kontinuierlich oder kategorisch) |
| Logistische Regression | 1 kategorische Variable | 1+ Variable(n) (kontinuierlich oder kategorisch) |
Logistische Regression SPSS vs. Lineare Regression
Aus der obigen Tabelle wird bereits deutlich worin sich logistische und lineare Regression im Wesentlichen unterscheiden: Bei der abhängigen Variable. Entscheidend ist hier das Skalenniveau der abhängigen Variable. Wenn die abhängige Variable intervallskaliert ist sollten man ein Logit Modell in Erwägung ziehen.
Beispiel lineare Regression: Vorhersage des Datenverbrauchs
Die Drahtlos AG ist ein Internetanbieter und möchte ihre Werbeanzeigen gezielter einsetzen. Dafür möchte das Unternehmen untersuchen, welche Faktoren den Datenverbrauch Ihrer Kunden vorhersagen. Untersucht werden sollen dabei die unabhängigen Variablen Alter, Geschlecht und Anschluss (Kabel oder DSL). Die abhängige Zielvariable ist die Menge der verbrauchten Daten und somit eine intervallskalierte kontinuierliche Variable. Für diese Analyse setzt die Drahtlos AG daher eine lineare Regression ein.
Logistische Regression SPSS – Kategorien mit Logit Modell vorhersagen
Wenn die abhängige Variable dagegen Kategorien enthält, ist die logistische Regression das richtige Verfahren für die Regressionsanalyse. In einer linearen Regression sagt das Regressionsmodell die Werte für die abhängige Variable anhand der unabhängigen Variablen vorher. In einer logistischen Regression dagegen werden die Wahrscheinlichkeiten für die Kategorien der abhängigen Variable anhand der unabhängigen Variablen modelliert. Hat die abhängige Variable nur zwei Kategorien (z.B. Kaufentscheidung: ja/nein), handelt es sich um eine binäre logistische regression.
Beispiel logistische Regression SPSS: Vorhersage der Kündigungen
Die Drahtlos AG möchte gerne seine Kundenbindung verbessern. Hierfür soll zuerst ermittelt werden, welche Kunden besonders häufig Ihren Vertrag kündigen. Die abhängige Variable ist also kategorisch mit 2 Gruppen (Vertrag gekündigt: ja/nein). Für diese Analyse soll deshalb eine binäre logistische Regression eingesetzt werden. Als mögliche Einflussfaktoren auf die Kündigungsrate sollen Alter, bisherige Vertragslaufzeit (gemessen in Monaten), Mindestvertragslaufzeit (1 Monat, 1 Jahr oder 2 Jahre) sowie Anschlussart (Kabel oder DSL) untersucht werden. Diese Variable stellen dementsprechend die unabhängigen Variablen im Logit Modell dar.
Ausgabe für die logistische Regression SPSS
Vor der Analyse wurden die Daten bereits auf Ausreisser sowie auf nicht-lineare Zusammenhänge geprüft. In der SPSS Ausgabe wird zuerst die Codierung der kategorischen Variablen aufgelistet:
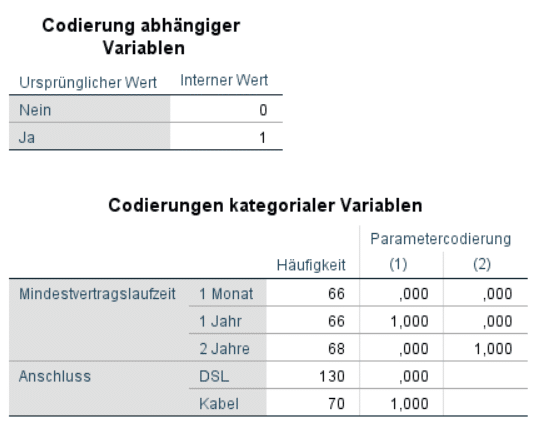
Für die unabhängige Variable werden Kündigungen (“Ja”) als 1 gewertet. Verbleibende Kündigungen werden als 0 codiert. Es wird im Logit Modell somit die Wahrscheinlichkeit für eine Kündigung vorhergesagt. Bezüglich der Mindestvertragslaufzeit werden monatliche Verträge mit “0” für beide Dummy-Variablen codiert. Die Effekte von einem Vertrag mit 1 Jahr und 2 Jahr werden somit mit monatlichen Verträgen verglichen.
Nach diesen Angaben zeigt die SPSS Ausgabe ein Logit Modell ohne unabhängige Variablen. Dieses Modell wird auch als Nullmodell bezeichnet.

Kunden die bei der Firma verbleiben (73%) sind häufiger als Kunden die kündigen (27%). Nehmen wir einmal an, wir müssten für jeden Kunden raten müssten ob dieser kündigt oder nicht. Dann hätten wir ohne weitere Information die höchste Trefferquote, wenn wir immer davon ausgehen, dass ein Kunde verbleibt. Das Nullmodell sagt daher auch für jeden Kunden vorher, dass diese nicht kündigen und bei der Firma verbleiben. Damit sagt das Nullmodell 100% aller verbleibenden Kunden korrekt vorher,kann aber keine einzige Kündigung vorhersagen (0% Genauigkeit). Dies führt zu einer Trefferquote von insgesamt 73%. Wenn wir nun unsere unabhängigen Variablen in Betracht ziehen erwarten wir, dass wir eine signifikant höhere Trefferquote erzielen als dieses Nullmodell. Wenn für die logistische Regression SPSS verwendet wird, können wir den Effekt der unabhängigen Variablen in der Ausgabe im Abschnitt für “Block 1” prüfen:
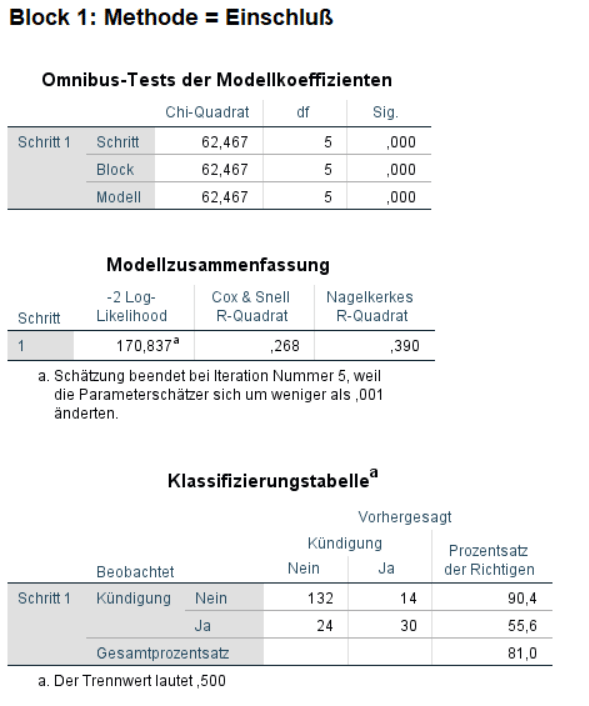
Tatsächlich schneidet das Modell mit unabhängigen Variablen besser ab als das Nullmodell im vorherigen Block, χ²(5) = 62,47, p < 0,001. Das Modell identifiziert verbleibende Kunden zu 90% korrekt. Kündigungen sagt das Modell immerhin in 56% der Fälle korrekt vorher. Insgesamt werden 81% der Fälle korrekt klassifiziert. In der folgenden Tabelle lässt sich der Einfluss der einzelnen unabhängigen Variablen überprüfen.
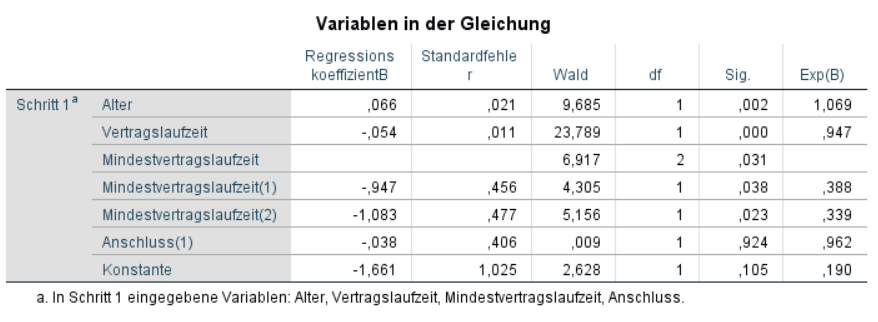
Interpretation der Regressionskoeffizienten
Tatsächlich hatte lediglich die Anschlussart keinen Einfluss auf die Kündigungsrate, odds ratio = 0,96, p = 0,92.
Ältere Personen hatten eine höhere Wahrscheinlichkeit zu kündigen: Für eine Steigerung im Alter von einem Jahr stieg die Chance um das 1,07-fache, p = 0,002. Kunden mit einer längeren Vertragslaufzeit hatten dahingegen eine geringere Chance zu kündigen. Für eine Steigerung in der Vertragslaufzeit von einem Jahr sank die Chance für eine Kündigung um 5%, odds ratio = 0,95, p < 0,001. Kunden mit einer Mindestvertragslaufzeit von einem Jahr (Dummy-Variable “1”) hatten ein 61% geringere Chance zu kündigen als Kunden mit einer monatlichen Mindestlaufzeit, odds ratio = 0,39, p < 0,04. Kunden mit einer Mindestvertragslaufzeit von zwei Jahren (Dummy-Variable “2”) hatten ein 66% geringere Chance zu kündigen als Kunden mit einer monatlichen Mindestlaufzeit, odds ratio = 0,34, p < 0,02.
Schlussfolgerungen ziehen für eine binäre logistische Regression
Diese binäre logistische Regression bildet die Grundlage für eine neue Marketingstrategie für die Drahtlos AG. Auf Basis der Ergebnisse wird beschlossen verstärkt Kampagnen zur Kundenbindung bei Risikogruppen einzusetzen. Somit werden nach der neuen Strategie Kampagnen zur Kundenbindung gezielt bei älteren Personen mit einer geringen bestehenden Vertragslaufzeit und einer monatlichen Mindestvertragslaufzeit eingesetzt.
Logistische Regression SPSS vs. Chi-Quadrat
Zuletzt wollen wir die logistische Regression mit dem Chi-Quadrat Test vergleichen. Ein Chi-Quadrat Test kann Zusammenhänge zwischen zwei kategorischen Variablen prüfen. Eine detaillierte Beschreibung vom Chi-Quadrat Test finden Sie in unserem Artikel zur SPSS Kreuztabelle.
Nehmen wir also an, wir wollen den Zusammenhang zwischen genau einer kategorischen unabhängigen Variable auf eine kategorische abhängige Variable betrachten. In diesem Fall bietet sich sowohl eine logistische Regression als auch ein Chi-Quadrat Test an. In der Regel werden beide Verfahren auch zu ähnlichen Schlussfolgerungen führen. Welchen Test sollten Sie nun aber verwenden? Das hängt von dem Ziel Ihrer Datenanalyse ab: Wenn Sie lediglich einen möglichen Zusammenhang zwischen den Variablen untersuchen möchten, ist ein Chi-Quadrat Test ausreichend. In solch einem Fall sollten Sie dem einfacheren Verfahren den Vorzug geben und das ist der Chi-Quadrat Test. Wenn Sie aber auch Vorhersagen erzeugen möchten und die Genauigkeiten dieser Vorhersagen beurteilen wollen, sollten Sie zu einer logistischen Regression greifen. Sobald Sie mehr als eine unabhängige Variable betrachten wollen (z.B. für Kontrollvariablen) bietet sich ohnehin ein Logit Modell an.
Zusammenfassung: So setzen Sie die logistische Regression (SPSS) sinnvoll ein!
In diesem Artikel sind wir auf die Anwendungsmöglichkeiten einer logistischen Regression eingegangen. Wir haben gezeigt wann man eine (binäre) logistische Regression sinnvollerweise einsetzen sollte und haben anhand eines Praxisbeispiels einen ersten Einblick in die praktische Anwendung eines Logit Modells gegeben. Ausserdem haben wir die Unterschiede von linearer Regression zu logistischer Regression einfach erklärt. Weiterhin haben wir die Unterschiede zum Chi-Quadrat Test besprochen.
Wir hoffen, dass Ihnen dieser Artikel einen Überblick über mögliche Anwendungsmöglichkeiten einer logistischen Regression gegeben hat. Wenn Sie weitere Unterstützung für Ihre statistische Auswertung benötigen, stehen Ihnen die Experten von Novustat jederzeit zur Verfügung!