Korrelationsanalysen sind eine nützliche Methode, um grundlegende Zusammenhänge zwischen Paaren von Variablen zu untersuchen. Diese Art von Analyse ist aber nur sinnvoll, wenn die untersuchten Variablen auf metrisches Niveau (für Persons r) oder auf ordinalen Niveau vorliegen (für Kendalls tau oder Spearmans Rho). Was aber, wenn man Zusammenhänge zwischen Variablen wie Geschlecht oder Religionszugehörigkeit untersuchen will? Solche Variablen sind kategorial und nominal. Für die Werte dieser Variablen gibt es also keine logische Reihenfolge der Werte. Eine Korrelationsanalyse ist dann nicht möglich. Glücklicherweise gibt es die SPSS Kreuztabelle als Alternative!
Kreuztabelle SPSS: Erste Wahl für den Zusammenhang zwischen Kategorien!
In diesem Fall kann man aber auf die Kreuztabelle in SPSS und den Chi-Quadrat Unabhängigkeitstest zurückgreifen. Wenn man für die Kreuztabelle SPSS verwendet, kann man zum einen Zusammenhänge zwischen zwei Variablen statistisch prüfen. Zusätzlich eignet sich die Kreuztabelle aber auch um Zusammenhänge zwischen Variablen intuitiv verständlich darzustellen. Wir möchten Ihnen in diesem Artikel deshalb eine verständliche Schritt-für-Schritt Anleitung für die SPSS Kreuztabelle an die Hand geben. Wenn Sie für Ihre statistische Auswertung allerdings lieber auf professionelle Hilfe zurückgreifen möchten, helfen unsere Experten Ihnen gerne weiter!
Dieser Artikel beantwortet folgende Fragen
- Wie erstellt man eine Kreuztabelle in SPSS?
- Kreuztabelle SPSS Interpretation: Wie interpretiert man einen Chi-Quadrat Test?
- Wie stellt man das Ergebnis einer Chi-quadrat Tabelle optimal grafisch dar?
Kreuztabelle in SPSS erstellen
Um den Nutzen einer Kreuztabelle zu verdeutlichen, betrachten wir folgendes Beispiel:
Das Start-Up C-Coach möchte Coaching zu Karrierethemen als Web-Service anbieten. Zunächst möche C-Coach das Interesse an solch einem Service abschätzen können. Daher hat C-Coach zunächst eine Umfrage durchgeführt. Dabei wurden Menschen in unterschiedlichen beruflichen Positionen befragt, ob Sie solch einen Service nutzen würden. Es soll also untersucht werden, ob ein Zusammenhang zwischen der beruflichen Situation und dem Coaching von C-Coach besteht. Hierfür soll für den Chi-Quadrat Test SPSS eingesetzt werden.
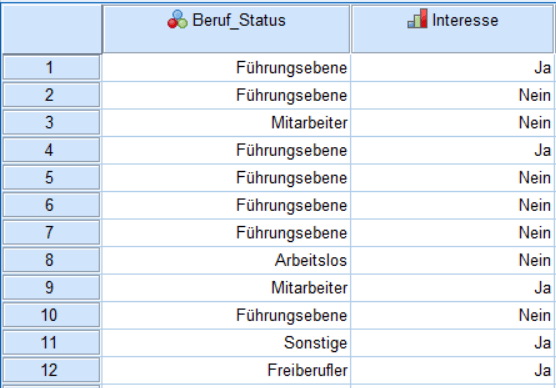
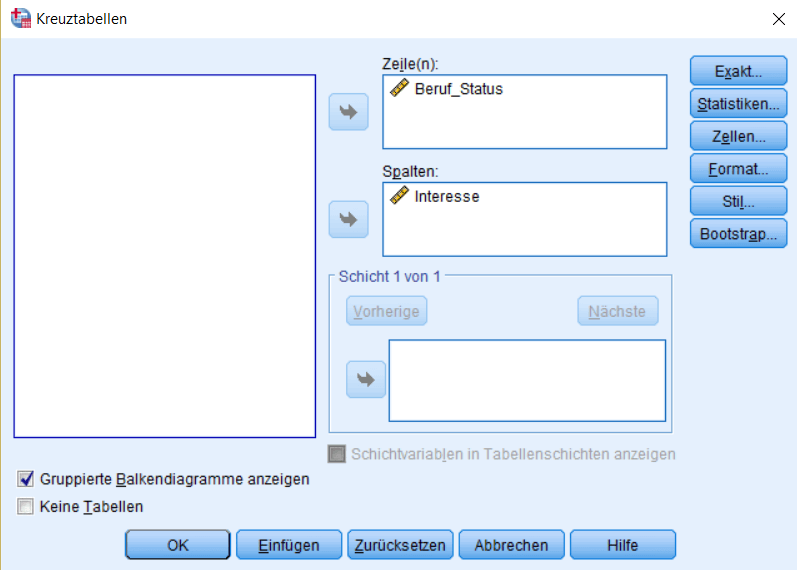
Diese Daten eignen sich hervorragend um in einer Kreuztabelle dargestellt zu werden und durch den Chi-Quadrat-Unabhängigkeitstest geprüft zu werden. Beides kann in SPSS über den Menüpunkt “Deskriptive Statistiken –> Kreuztabellen” erledigt werden. Im Menü sollte dann jeweils eine gruppierende Variable den Spalten und Zeilen zugeteilt werden.
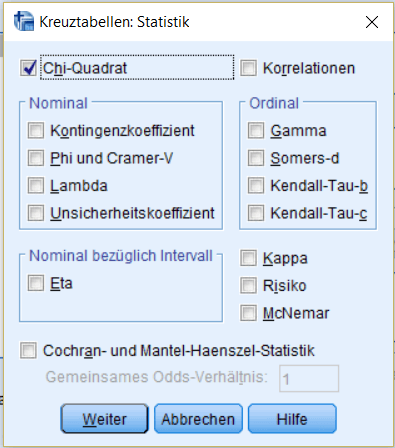
Unter „Statistiken“ kann dann der Chi-Quadrat-Test angefordert werden.
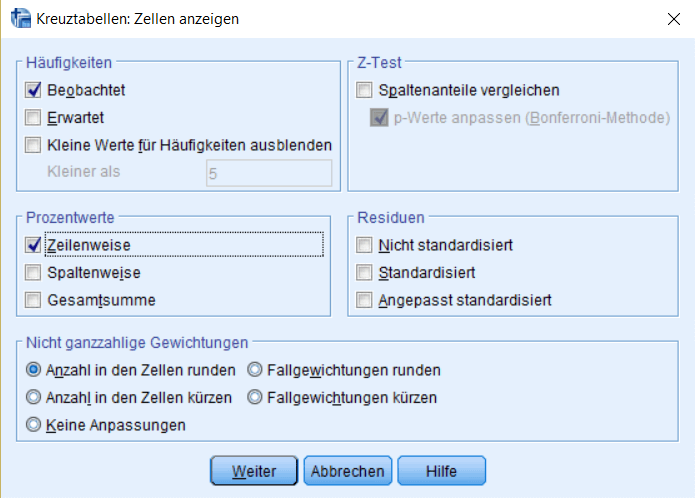
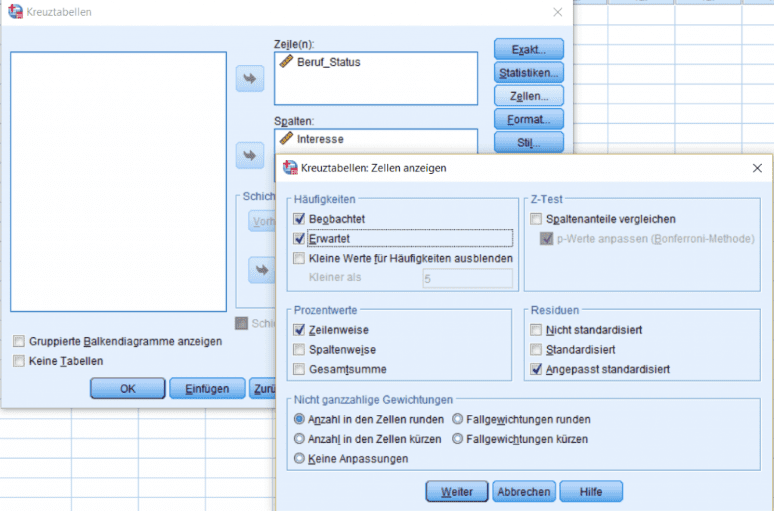
Unter dem Menüpunkt „Zellen“ befinden sich verschiedene Anzeigeoptionen für die SPSS Kreuztabelle. Wir werden später noch auf diese Optionen zurückkommen. Für unser Beispiel möchten wir erst einmal nur wissen, wie sich das Interesse per Berufsgruppe (Variable für Zeile) verteilt. Daher fordern wir noch die zeilenweisen Prozentwerte an.
Die Ausgabe zeigt zunächst die Anzahl aufgeteilt nach den gruppierenden Variablen (beruflicher Status und Interesse).
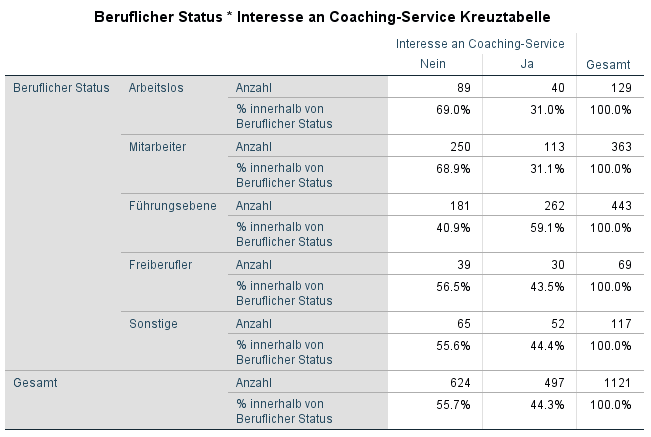
Danach folgt die Chi-Quadrat-Test SPSS Ausgabe. Unten ist die Chi-Quadrat Tabelle für den Beispieldatensatz abgebildet.
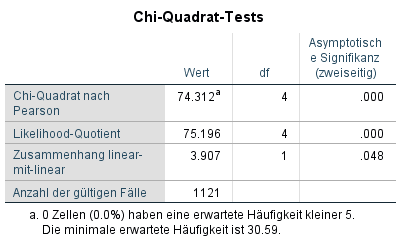
Wie in der Chi-Quadrat Tabelle zu sehen ist, fällt der Chi-Quadrat Test signifikant aus, χ2 (4) = 74,31, p < 0,001. Es gibt also einen Zusammenhang zwischen der beruflichen Situation der Teilnehmer und dem Interesse an dem Coaching-Service. Häufig wird die Analyse an dieser Stelle beendet. Tatsächlich haben wir aber eine interessante Frage noch gar nicht beantwortet: Wie genau hängen die Variablen miteinander zusammen?
Kreuztabelle SPSS Interpretation mit Residuen ermöglichen!
Um diese Frage zu klären fordern wir erneut dieselbe SPSS Kreuztabelle an. Diesmal fragen wir aber zusätzliche Werte unter dem Menüpunkt „Zellen“ an. Für die Folgeuntersuchung auf einen signifikanten Chi-Quadrat Test empfehlen wir, sowohl die erwarteten Werte anzufragen als auch die angepassten Residuen.
Die Ausgabe zeigt nun diese zusätzlichen Werte an.
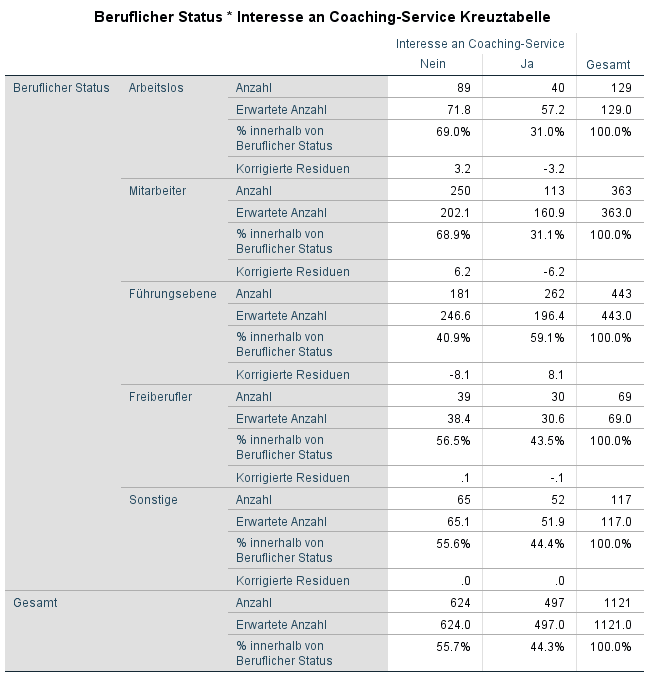
Die erwartete Anzahl zeigt die Anzahl für eine Verteilung in der Berufsstatus und Interesse vollständig unabhängig voneinander wären. Die Abweichung von der beobachteten Anzahl und der erwarteten Anzahl wird von den Residuen angegeben. Angepasste Residuen sind Residuen die bereits standarisiert wurden. Diese angepassten standarisierten Residuen können deshalb als gewöhnliche Z-Werte behandelt werden. Für jedes Residuum kann also anhand einer Tabelle der Standardnormalverteilung der entsprechende p-Wert ermittelt werden.
Dieser p-Wert sollte allerdings noch für multiples Testen korrigiert werden. Am einfachsten geschieht dies durch eine Bonferroni-Korrektur. In diesem Fall wir für jede der 5 Berufsgruppen ein Test durchgeführt (Interesse: ja versus nein). Für eine Bonferroni-Korrektur sollte also jeder p-Wert mit 5 multipliziert werden. Es existieren allerdings auch fortgeschrittene Verfahren zur Korrektur für multiples Testen wie das Benjamini-Hochberg-Verfahren. Diese Verfahren verfügen über eine bessere Teststärke (Power). Diese empfehlen sich besonders bei einer hohen Anzahl an Vergleichen. Novustat hilft Ihnen mit einer Statistik Beratung gerne weiter.
In dem obigen Beispiel fällt bei Analyse der Residuen auf, dass Arbeitslose und einfache Mitarbeiter signifikant häufig kein Interesse an dieser Form des Einzelcoachings hatten (korrigierte ps < 0,01). Mitglieder der Führungsebene zeigten dagegen signifikant häufig Interesse an dieser Form des Einzelcoachings (korrigiertes p < 0,001). Die Aufmachung des Einzelcoaching hat also vor allem Mitglieder der Führungsebene angesprochen.
Kreuztabelle SPSS Interpretation: Effektive Darstellung mit Graphen
Für einen professionellen Bericht sollte man Graphen einsetzen um die Ergebnisse aus einem Chi-Quadrat-Test SPSS zu verdeutlichen. Hierfür empfiehlt sich ein Balkendiagramm. Passende Balkendiagramme kann man in SPSS unter der Option „Grafik Diagrammerstellung“ erstellen.
Bei Balkendiagrammen besteht die Wahl zwischen einem gestapelten oder gruppierten Balkendiagramm. Diese Wahl hängt davon ab, welche Aspekte im Vordergrund stehen sollen. Unsere Empfehlung ist in der folgenden Tabelle zusammengefasst:
| Diagramm | Symbol in SPSS | Besonders geeignet für | Beispiel |
| Gruppiertes Balkendiagramm |  | Vergleichen von absoluten Häufigkeitsverteilung | Wie viele Teilnehmer per Berufsgruppe waren an dem Service interessiert? |
| Gestapeltes Balkendiagramm |  | Vergleich von relativen Anteilswerten je Kategorie | Wie viel Prozent der jeweiligen Berufsgruppen waren an dem Service interessiert? |
In diesem Fall interessiert uns wie viel Prozent in jeder Berufsgruppe an dem Coaching-Service interessiert wären. Wir entscheiden uns also für ein gestapeltes Balkendiagramm. Um relative Prozentwerte anzuzeigen, wählen Sie unter „Diagrammeigenschaften“ für die Balken die Statistik „Prozentsatz ()“ aus. Um die Prozentwerte als relative Werte je Kategorie anzuzeigen, wählen Sie dann noch unter „Parameter festlegen“ die Option „Gesamt für jede X-Achsen-Kategorie“.
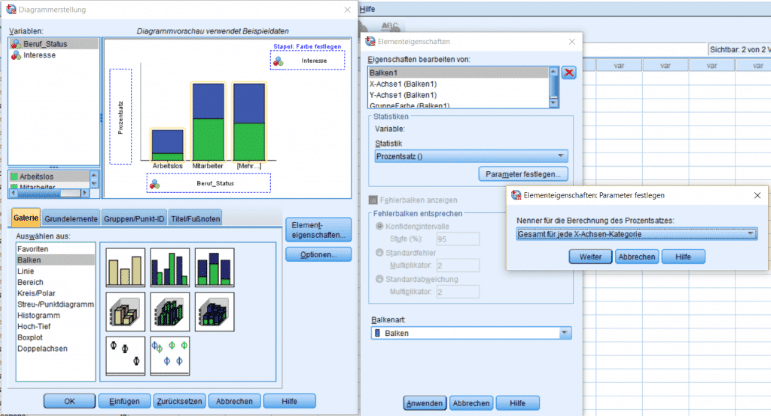
Für ein Diagramm mit 5 oder mehr Kategorien empfiehlt es sich ausserdem das Diagramm zu transponieren.
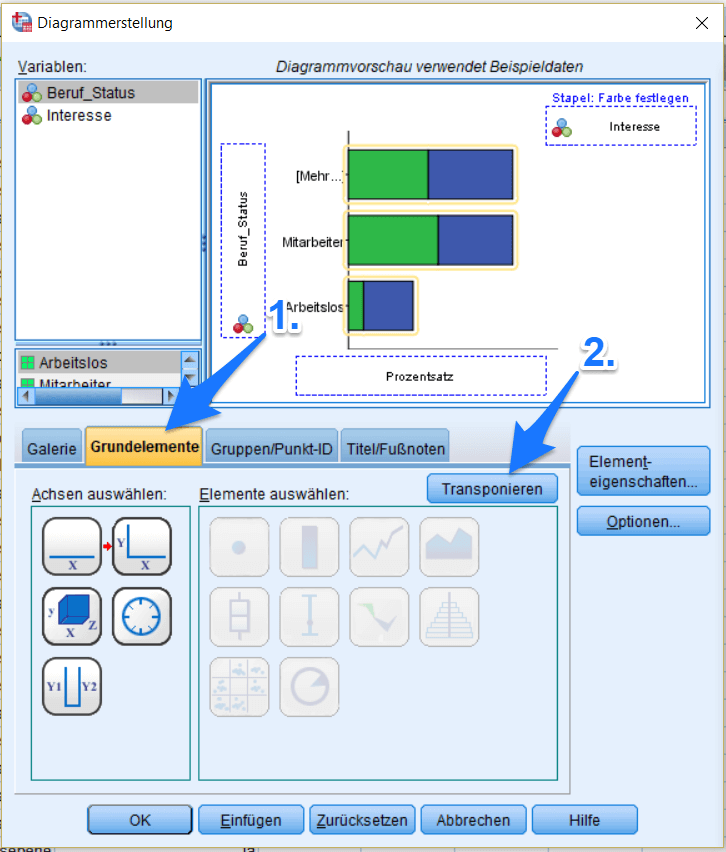
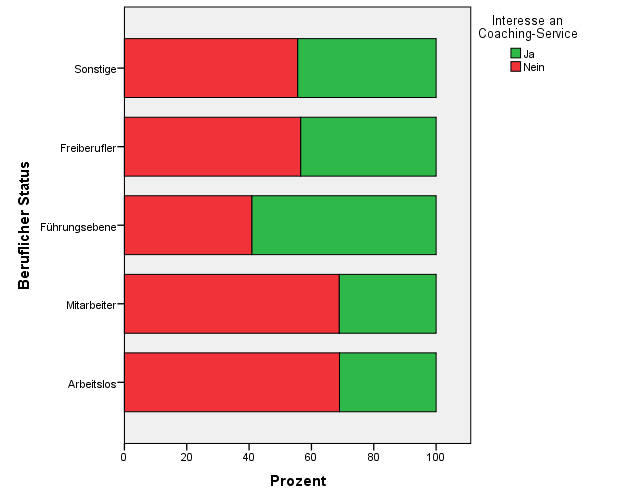
Kreuztabelle SPSS: Effekte zwischen kategorischen Variablen schnell analysieren
Kreuztabellen stellen ein Standardwerkzeug für die Analyse von Zusammenhängen von Variablen dar. Dies gilt ganz besonders für nominale Variablen, für die eine Korrelationsanalyse nicht möglich ist. In diesem Artikel haben wir Ihnen gezeigt, wie Sie eine Analyse mit Kreuztabelle schnell, einfach und auf professionellen Standard durchführen. Dabei haben wir alle Schritte bis zur graphischen Darstellung aufgezeigt. Wir hoffen, dass Sie wir Ihnen mit diesem Artikel für Ihre nächste Analyse mit Kreuztabellen unterstützen konnten!
Durch Kreuztabellen aufgedeckte Zusammenhänge können häufig auch das Sprungbrett sein um komplexe Zusammenhänge aufzudecken, etwa durch den Einsatz von anspruchsvolleren Verfahren wie logistischer Regression. Unsere Experten von Novustat beraten Sie hierzu gerne und helfen Ihnen das Maximum aus Ihren Daten zu holen!
