Die bivariate Datenanalyse beschreibt Methoden zur Auswertung von Zusammenhängen zwischen Merkmalen von zwei Variablen. Sie orientiert sich im Wesentlichen am Konzept der Kovarianz aus der Wahrscheinlichkeitstheorie. Im Folgenden werden zunächst die theoretischen Grundlagen erläutert, bevor die Korrelation in SPSS erläutert wird. Daran anschliessend werden die Kategorien der Korrelationsmasse vorgestellt, bevor diese anhand eines Beispiels bestimmt und die gewonnenen Daten interpretiert werden.
Sollten Sie Unterstützung bei Ihrer Statistik-Auswertung mit SPSS benötigen, helfen unsere Statistiker Ihnen gerne weiter. Kontaktieren Sie uns für eine kostenlose Beratung & ein unverbindliches Angebot.
Kovarianz und Korrelation
Das mathematische Konzept, auf dem die Korrelationsanalyse aufbaut, bilden paarweise verteilte, abhängige Zufallsvariablen. Hier ist zwischen der Kovarianz
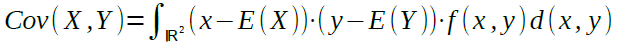
und der Korrelation
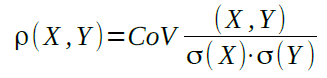
zu unterscheiden. Die Kovarianz ist zwar eine Kennzahl, aufgrund fehlender Beschränkung ist sie jedoch keine Masszahl und lässt daher keine Interpretation zu.
E(X) beschreibt den Erwartungswert und σ(X) die Standardabweichung der Zufallsvariablen X.
Um für die Analyse einer Korrelation in SPSS zu nutzen, orientiert man sich folgerichtig an der Korrelationsformel und testet die Hypothese: „Zwischen den Variablen X und Y besteht ein signifikanter Zusammenhang“ gegen die Nullhypothese: „Die Variablen sind voneinander unabhängig“.
Das Testverfahren wird demnach auch Unabhängigkeitstest genannt und die ermittelte Teststatistik basiert auf der t-Verteilung (Student-Verteilung).
Sie möchten eine Korrelationsanalyse in SPSS durchführen, benötigen dabei aber Unterstützung? Unsere Statistiker helfen Ihnen gerne jederzeit weiter! Kontaktieren Sie uns und geniessen Sie eine persönlich auf Sie zugeschnittene Unterstützung bei der SPSS Auswertung!
Skalierung von Daten
Zunächst gilt zu beachten, dass in der deskriptiven Statistik drei Skalenniveaus unterschieden werden. Da SPSS sie auf Basis numerisch erfasster Daten auswertet, ist bei der SPSS Auswertung auf die Skalierung der Daten zu achten.
- Nominale Skalen – in diese Gruppen fallen alle Merkmale, deren Ausprägungen durch nur Worte ausgedrückt werden und zwischen denen keine Rangfolge besteht (Geschlecht, Haarfarbe).
Die numerische Repräsentation dient hier nur der Zuordenbarkeit (z.B. ‚1‘ = männlich; ‚2‘ = weiblich). - Ordinale Skalen – in diese Gruppe fallen Merkmale, bei denen zwischen den verschiedenen Ausprägungen eine eindeutige Rangfolge existiert (Grad des Vertrauens, Steuerklasse, Altersgruppen).
Eine numerische Codierung erfasst die Rangfolge und ermöglicht eine Reihung. - Metrische (oder: kardinale) Skalen – diese Gruppe umfasst alle Merkmale, deren Ausprägungen numerische Werte sind (Alter, Einkommen, Temperatur) und deren Abstände berechenbar sind; eine Codierung ist damit nicht notwendig.
Für Kreuztabelle und Korrelation SPSS richtig nutzen
Um für die Berechnung der Korrelation SPSS zu nutzen, kann man, abhängig vom Skalenniveau der Variablen, zwei Wegen folgen: im Falle von metrischen (kardinalen) bzw. ordinal skalierten Variablen via „Analysieren → Korrelationen → Bivariat“
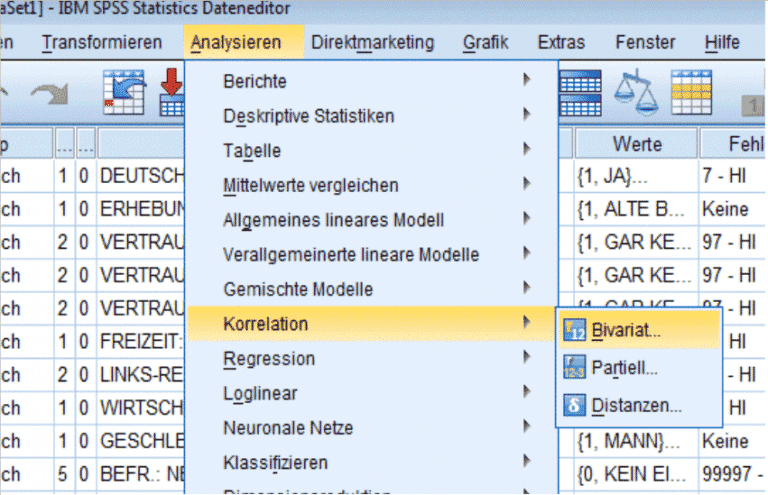
Zunächst werden die zu untersuchenden Merkmale aus der Liste gewählt, danach das gewünschte Korrelationsmass – die Auswahl umfasst die Koeffizienten Kendalls Tau-b, Pearson und den Rangkorrelationskoeffizienten nach Spearman.
Sind die Variablen nominal und/oder ordinal skaliert und möchte man die Darstellung einer Kreuztabelle in SPSS nutzen, folgt man dem Pfad: „Analysieren → deskriptive Statistiken → Kreuztabellen“. Hier werden zunächst ebenfalls die zu untersuchenden Merkmale gewählt. Der Button „Statistiken“ ruft nun eine deutlich umfangreichere Übersicht an Korrelationsmassen auf, gegliedert in Kategorien (gemäss Skalierung der Daten) und nach den Kennzahlen Chi Quadrat und Korrelationen (Spearman, Pearson).
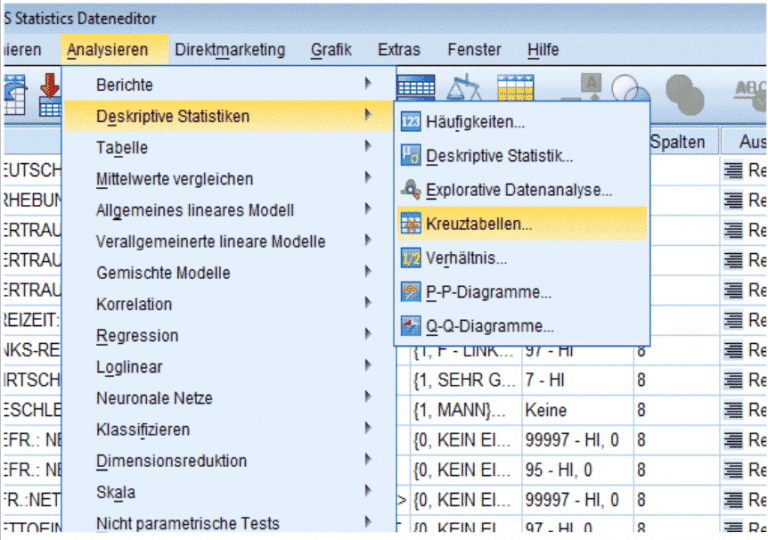
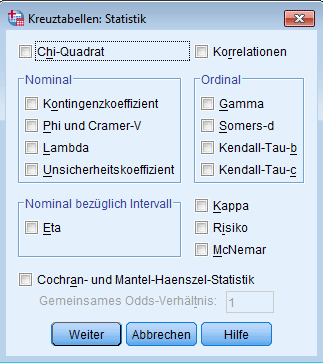
Kreuztabelle und Korrelation: SPSS und Auswahl der Korrelationskoeffizienten
Je nach Skalenpaarung ist ein anderes Korrelationsmass zu bestimmen und unterschiedlich zu interpretieren.
- Metrische (kardinale) Paarung – liegt die Paarung zweier metrisch (kardinal) skalierter Merkmale vor, wird der Korrelationskoeffizient nach Pearson herangezogen, bevorzugt über den Pfad: „Korrelationen → Bivariat“
- Ordinale Paarung – liegt eine Paarung ordinal skalierter Merkmale vor, können entweder der Rangkorrelationskoeffizient nach Spearman oder alternativ die Masse Gamma und Kendall-Tau bestimmt werden. Während Spearman auf dem Korrelationskoeffizienten aufbaut, liegt Gamma und den Taus lediglich die Rangfolge selbst zu Grunde.
Im Falle einer Paarung ordinaler und metrischer (kardinaler) Merkmale, kann diese nach erfolgter Herabstufung der metrischen Variable wie eine ordinale Paarung behandelt werden. - Nominale Paarung – liegt eine Nominale Paarung vor, lässt sich kein gerichtetes Mass bestimmen, lediglich die Assoziationsmasse Phi und Cramer-V . Diese bauen im Wesentlichen auf der Testgrösse Chi-Quadrat auf und sind über die zweite Option der Kreuztabelle abrufbar.
- Nominal & metrisch (kardinal) – im Fall einer solchen Paarung wird das kardinal skalierte Merkmal nicht herabgestuft, da der Informationsverlust zu gross wäre. Stattdessen wird zu jeder Ausprägung eine Gruppe gebildet und deren jeweilige Streuung ermittelt. Das Verhältnis wird durch den ETA-Koeffizienten ausgedrückt, der wiederum über die Option der Kreuztabelle abrufbar ist.
Kreuztabelle und Korrelation: SPSS und Anwendung der Korrelationskoeffizienten
Wie beschrieben sind abhängig von der Skalenpaarung in SPSS unterschiedliche Korrelationskoeffizienten zu bestimmen und unterschiedlich zu interpretieren.
- Korrelationskoeffizienten nach Pearson und Spearman – sie geben eine linearen Proportionalitätsfaktor an und können als linearer (positiver oder negativer) Zusammenhang interpretiert und mittels Streudiagramm dargestellt werden.
- Kontingenzmasse, Phi, Cramer-V – sie geben für eine nominale Paarung an, wie stark diese voneinander abhängen. Der Koeffizient Phi wird hierbei ausschliesslich für 2×2 Tabellen verwendet.- Bei nominalen Paarungen ist keine analytische Interpretation möglich.
- Kendalls Tau, Gamma – diese Koeffizienten geben die Stärke der Konkordanz, also einer übereinstimmenden Entwicklung der Werte an. Hier ist ebenso keine funktionalanalytische Interpretation möglich.
- ETA – da hier die Streuungen der gesamten Stichprobe und gebildeter Gruppen verglichen werden, ist keine gerichtete Aussage möglich. Der Zusammenhang wird hier als Einfluss des nominalen Merkmals (z.B. Geschlecht) auf das metrische Merkmal (z.B. Nettoeinkommen) interpretiert.
Korrelation: SPSS und Interpretation der Korrelationskoeffizienten
Bivariate Statistik: Zwei intervallskalierte Variablen
Das folgende Beispiel einer (nicht-repräsentativen) Umfrage zeigt, wie eine Korrelation SPSS nutzend ausgewertet und die Ergebnisse der Korrelationsanalyse interpretiert werden.
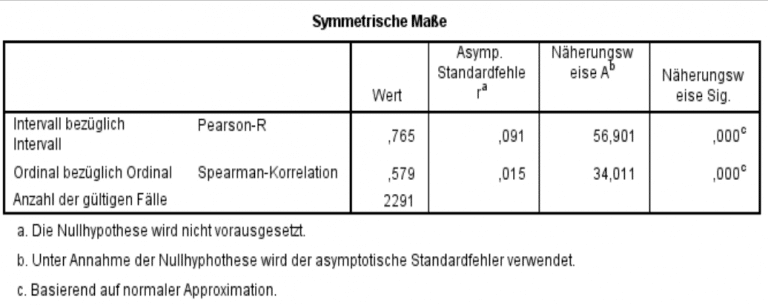
In der ersten Spalte finden sich die Werte der Korrelationskoeffizienten nach Pearson und Spearman – die Abweichung erklärt sich durch die bei Spearmans Ansatz zugrunde gelegte Rangfunktion; das bedeutet, dass der Ranglistenplatz eines Wertes betrachtet wird, anstatt des Wertes selbst. Ob der zwölfte Wert also 1000 oder 2500 beträgt, beeinflusst den Rang nicht, jedoch die bei Pearson betrachtete Kovarianz.
Je nach Unterscheidung handelt es sich also um einen mittleren (bis ±0,7; siehe Spearman mit ,579) bzw. starken Zusammenhang (ab ±0,7; Pearson mit ,765) zwischen den betrachteten Merkmalen. Da die asymptotische Signifikanz in der rechten Spalte in beiden Fällen mit ,000 kleiner als 5% ist, kann Nullhypothese verworfen und die Forschungshypothese angenommen werden, wonach ein hoch signifikanter Zusammenhang besteht.
Bivariate Statistik: Zwei ordinal skalierte Variablen
Für eine ordinale Paarung kann zum einen Kendalls Tau ermittelt werden, zum anderen der vereinfachte Gamma-Koeffizient – wie zuvor finden sich in der linken Spalte die Werte der Korrelationsanalyse, in der rechten Spalte die asymptotische Signifikanz. Der Unterschied zwischen den Korrelationen beruht darauf, dass Kendalls Tau sogenannte Tie-Ins berücksichtigt, also Wertepaare, bei denen sich nur ein Wert verändert. Gamma betrachtet diese nicht.
In beiden Fällen kann wiederum ein hoch signifikanter Zusammenhang angenommen werden, der zudem mittelmässig bis etwas stärker ausgeprägt ist.

Bivariate Statistik: Zwei nominal skalierte Variablen
Im Falle einer nominalen Paarung entfallen in der Tabelle die Standardfehler, da diese auf der Standardabweichung basieren und somit eine Rangordnung voraussetzen. In der linken Spalte finden sich die Werte der Korrelation, in der rechten die Signifikanz.
Der erhebliche Unterschied der Werte beruht wie zuvor auf der Konstruktion der Werte – während beide Koeffizienten auf Chi-Quadrat aufbauen, berücksichtigt Phi zusätzlich lediglich die Anzahl der Befragten, Cramer-V hingegen die Anzahl der Ausprägungen beider Variablen.

Den Werten nach kann in beiden Fällen angenommen werden, dass eine signifikante Abhängigkeit der Merkmale voneinander besteht, die je nach Mass eher schwach oder sehr stark ausgeprägt ist.
Bivariate Statistik: Eine intervallskalierte Variable mit einer nominal skalierten Variable
Im Gegensatz zu den bisherigen Auswertungen ist für den ETA-Koeffizienten keine Signifikanz angegeben – diese liesse sich im Zuge einer Varianzanalyse in SPSS ermitteln. Der Koeffizient von 0,353 ist an dieser Stelle entscheidend, da das metrisch skalierte Einkommen als vom Geschlecht abhängig betrachtet wird. Der Einfluss, den das Geschlecht (als unabhängige Variable) auf das Nettoeinkommen (abhängige Variable) hat, ist damit ein eher schwacher.

Häufig gestellte Fragen
Weiterführende Links
Cleff (2008): Deskriptive Statistik und moderne Datenanalyse