In der Statistik erklärt man mit Variablen die Ausprägung anderer Variablen. Allerdings kommt es bei Analysen immer wieder vor, dass eine Variable nicht die Ausprägung, sondern den Effekt einer anderen Variablen auf eine gemeinsame abhängige Grösse beeinflusst. Zum Beispiel: Wirken politische Massnahmen in verschiedenen Regionen unterschiedlich? Bringt eine Stunde Arbeitszeit mehr Ertrag, wenn Mitarbeiter höhere Qualifikationen aufweisen? – Die Interpretation solcher Interaktionseffekte ist nicht nur sehr interessant, sondern auch wichtig, da versteckte Interaktionen zu den häufigsten Fehlern bei statistischen Analysen gehören.
Sie möchten Interaktionseffekte in Stata verstehen und interpretieren lernen? Sie brauchen in anderen Bereichen professionelle Stata Hilfe? Wenden sie sich hierzu an uns für eine kostenlose Erstberatung.
Dieser Beitrag behandelt eine einfache Interaktion und ihre Modellierung in Rahmen einer Regressionsanalyse. Wir betrachten und interpretieren Haupteffekt und Interaktionseffekte anhand eines Beispiels im Statistikprogramm Stata.
Was ist ein Interaktionseffekt?
Ein (einfacher) Interaktionseffekt ist eine technische Repräsentation der sogenannten Moderation. Eine Moderation liegt vor, wenn die Stärke des Effektes einer unabhängigen Variablen von der Ausprägung einer anderen unabhängigen Variablen beeinflusst wird.
Ein (fiktives) Beispiel: Wir möchten den Verschuldungsgrad eines Unternehmens (debt) als Funktion seiner Grösse (size) berechnen. Wir gehen davon aus, dass die Unternehmensgrösse anders ins Gewicht fällt, wenn das Unternehmen viel investiert (invest) oder börsennotiert ist (listed). Diese Zusammenhänge lassen sich durch die folgende Formel beschreiben:
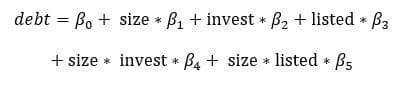
Mathematisch gesehen ist eine Interaktion immer symmetrisch, d.h. jede der beiden beteiligten Variablen moderiert die Wirkung der jeweils anderen. Welche der beiden Moderationen inhaltlich Sinn macht, ist eine theoretische Entscheidung und hängt von der Fragestellung ab.
Stata bietet dafür vielfältige Lösungen und Novustat unterstützt Sie bei allen Schritten Ihrer Studie: konzeptuelle Ausarbeitung, Erstellung eines Modells und die Umsetzung, zum Beispiel einer Moderation in Stata. Wenden Sie sich dafür an unsere statistische Beratung.
Modellierung einer Interaktion in Stata
Unabhängig vom verwendeten statistischen Programm lassen sich einfache Moderationen mittels zweiseitiger Interaktionsvariablen modellieren. Dabei wird eine neue Variable berechnet, die das Produkt der beiden Ausgangsvariablen darstellt. In Stata sieht das wie folgt aus:

Diese Interaktionsvariable wird dann zusätzlich zu den Haupteffekten in das Modell aufgenommen. Alternativ kann in Stata die sogenannte Faktoren-Schreibweise verwendet werden. Man platziert dabei zwei Rauten (##) zwischen den Variablen, die in einer Interaktionsbeziehung stehen sollen. Mit einer Raute (#) werden Haupteffekte nicht in das Modell aufgenommen. Um die Faktoren-Schreibweise zu nutzen, sind die Variablen im Modell zwingend als kategorial (i.) oder metrisch (c.) zu kennzeichnen.
Die Modellierung der Interaktionseffekte in unserem Beispiel sieht dann entsprechend der gewählten Methode so aus:

oder alternativ:
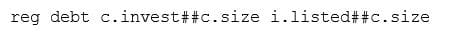
Interpretation: Interaktionseffekte in Stata
Betrachten wir nun den Output. Die Berechnungen wurden mit simulierten Daten durchgeführt. Die Zahlen haben somit keine empirische Entsprechung und dienen lediglich der Präsentation.
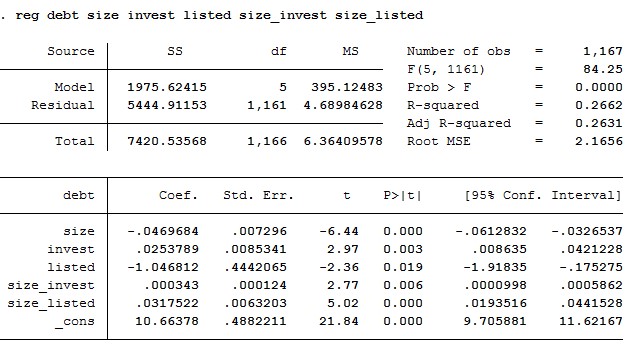
Die einfachste Möglichkeit, eine Interaktion zu interpretieren, ist die Koeffizienten gemäss der oberen Formel zu verrechnen. Hier ist darauf zu achten, dass in einem Modell mit Interaktionstermen Haupteffekte nicht mehr an sich aussagekräftig sind und nur in Kombination mit den Interaktionskoeffizienten interpretiert werden. In unserem Beispiel hat die Grösse eines Unternehmens (size) einen signifikanten negativen Einfluss auf den Verschuldungsgrad. Je grösser das Unternehmen, desto weniger verschuldet ist es. Aber auch der Interaktionskoeffizient size_invest ist signifikant. Seine Richtung ist gegenläufig; die Grösse fällt also weniger ins Gewicht, wenn das Unternehmen viel investiert. Für jede Einheit Investition müssen wir 0,0003 zu dem Haupteffekt der Grösse dazurechnen, was einen negativen Koeffizienten ausgleicht. Darüber hinaus fällt der Grösseneffekt auch bei börsennotierten Unternehmen schwächer aus, denn auch size_listed ist signifikant und positiv, zeigt also in die andere Richtung. Folglich bedingt die Zunahme um eine Einheit ‚Grösse‘ hier nicht 0,047, sondern 0,015 (=-0,047+0,032) weniger Verschuldungspunkte.
Zu beachten ist jedoch, dass ein solches lineares Herangehen in nichtlinearen Modellen wie z.B. in den beliebten logistischen oder Probit Regressionen nicht zulässig ist. In so einem Fall ist die Berechnung von sogenannten marginalen Effekten mittels des Befehls margins zu empfehlen. Aber auch bei linearen Modellen kann diese Anwendung sinnvoll sein, da sich hier übersichtliche grafische Darstellungsmöglichkeiten nutzen lassen.
Margins ist ein sogenannter „postestimate“-Befehl, d.h. er muss immer unmittelbar nach der betreffenden Regression durchgeführt werden. An dieser Stelle ist wichtig zu erwähnen, dass margins nur dann korrekt funktioniert, wenn die Faktoren-Schreibweise verwendet wurde!
Interpretation: Interaktionseffekte bei metrischen und binären Variablen
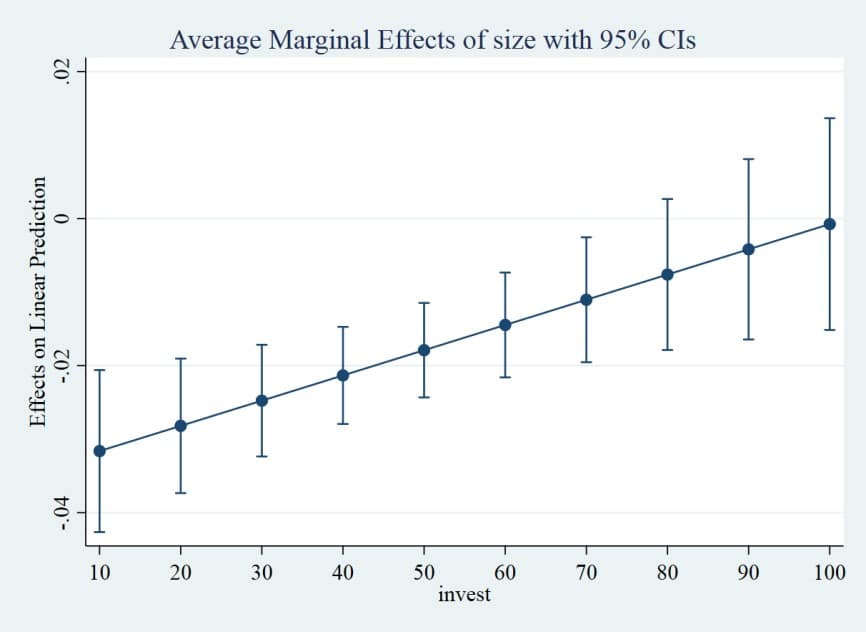
Für unsere erste Interaktion mit einer metrischen Variablen berechnen wir den geschätzten marginalen Effekt der Grösse abhängig von unterschiedlichen Ausprägungen des Investitionsvolumens. Der Zusatzbefehl marginsplot gibt eine entsprechende grafische Darstellung aus. In den Klammern wird die Skalierung der X-Achse, also die Spanne der Variable invest angegeben (hier fiktive 1 bis 100).

In unserem Beispiel sehen wir den Effekt der Grösse mit zunehmenden Investitionen gegen Null wandern, er wird also schwächer. Der Effekt ist in jenen Bereichen signifikant, in denen die Konfidenzintervalle nicht die Nulllinie schneiden. Es handelt sich um die sogenannten durchschnittlichen marginalen Effekte (AME). Stata erlaubt jedoch unterschiedliche Spezifikationen. Da wir ein lineares Modell als Beispiel nutzen, entspricht der marginale Effekt dem üblichen linearen Effekt.
Bei einer binären Variablen, bei der nur zwei Effektwerte verglichen werden, kann es von Interesse sein, ob der unterschiedliche Effekt der Grösse den absoluten Verschuldungsgrad zwischen notierten und nicht notierten Unternehmen beeinflusst. Interaktionen lassen sich also immer aus zwei Perspektiven interpretieren. Bei dieser Fragestellung empfiehlt sich eine andere Darstellungsweise, bei der die Schätzwerte der Verschuldung (also der abhängigen Variablen) in Abhängigkeit von der Grösse und getrennt nach beiden Unternehmensarten abgebildet werden.
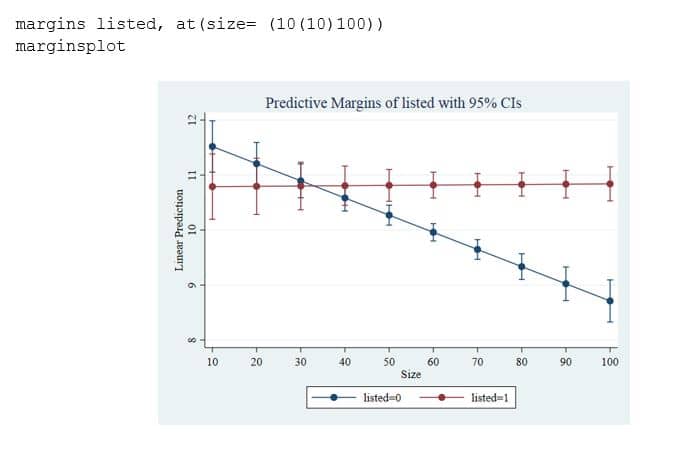
Die Abbildung verdeutlicht: Der Abstand zwischen den beiden Linien steigt konstant an. Das ist ein Indiz dafür, dass grössere börsennotierte Unternehmen deutlich höher verschuldet sind als nicht gelistete Unternehmen. In den Bereichen, in denen sich die Konfidenzintervalle überschneiden, ist der Unterschied nicht signifikant. Es lassen sich demnach keine Unterschiede bei kleinen Unternehmen feststellen.
Fazit
In diesem Beitrag haben wir mittels Stata das Beispiel einer einfachen Moderation dargestellt und den Effekt zwischen zwei Variablen behandelt. In komplexeren Moderationen in Stata sind Modellierung und Interpretation von Interaktionseffekten nicht mehr so intuitiv umsetzbar wie im dargestellten Beispiel. Wichtig ist hier ein gutes konzeptuelles Modell, denn Ergebnisse müssen plausibel sein. Stata bietet dafür vielfältige Lösungen und Novustat unterstützt Sie bei allen Schritten Ihrer Studie: konzeptuelle Ausarbeitung, Erstellung und Umsetzung eines Modells. Wenden Sie sich dafür gerne an uns über unsre Anfrageformular.