Neben dem rein wissenschaftlichen Erkenntnisgewinn ist gerade das Wissen um kausale Zusammenhänge der Schlüssel für eine praxisorientierte Anwendung von Forschungsergebnissen. In diesem Beitrag möchten wir die zentralen Herausforderungen datenbasierter Kausalanalysen erläutern und Impulse geben, wie man diesen Herausforderungen mit geeigneten statistischen und theoretischen Verfahren begegnet kann.
Zögern Sie nicht, uns zu kontaktieren, wenn Sie Fragen zur Analyse kausaler Zusammenhänge oder Datenauswertung haben. Wenden sie sich einfach an uns für eine Statistik Beratung. Unsere Expert*innen helfen Ihnen gerne, Ihr Projekt im Handumdrehen zum Erfolg zu führen!
Ziel einer Datenanalyse kann entweder eine Prognose mittels Predictive Modeling oder die Aufklärung von kausalen Zusammenhängen sein. Beide Anwendungsbereiche stellen zum Teil unterschiedliche Anforderungen an die Methodenwahl. So kommt es bei der Suche nach Kausalitäten weniger auf die Präzision der Schätzung und die allgemeine Erklärungskraft der Modelle an, sondern mehr auf das richtige Forschungsdesign und korrekte Kontrolle von beobachteten und unbeobachteten Störvariablen.
- Spiegelt der Zusammenhang, den ich statistisch beobachte, reale Prozesse wider?
- Würde sich das Ergebnis zwangsläufig ändern, wenn ich die Möglichkeit hätte, die eine andere Grösse zu manipulieren?
Korrelation vs. Kausalität
Von einer Korrelation spricht man, wenn ein statistischer Zusammenhang zwischen zwei Variablen beobachtbar ist, z. B. in Form eines signifikanten Korrelationskoeffizienten. Das bedeutet, dass bestimmte Werte einer Variablen mit einer höheren Wahrscheinlichkeit zusammen mit bestimmten Werten einer anderen Variablen auftreten. Mit anderen Worten: Eine Variable kann als Funktion einer anderen Variable beschrieben werden. Die Kenntnis dieser Beziehung mag oft ausreichen, wenn man nur an einer Prognose interessiert ist, sie kann aber sehr irreführend sein, wenn Aussagen über kausale Zusammenhänge im Mittelpunkt stehen.
Eine kausale Beziehung setzt immer eine statistisch signifikante Korrelation voraus, nicht aber umgekehrt. Das berühmte Beispiel mit Störchen und den Babys haben wir bereits gebracht und damit die Korrelation ohne Kausalität beschrieben. Kausalität setzt voraus, dass es für den beobachteten Zusammenhang eine plausible Erklärung gibt. Kausale Zusammenhänge sind oft komplex und laufen über Mechanismen. Diese müssen benennbar und ihrerseits (zumindest prinzipiell) testbar sein. Eine unabdingbare Voraussetzung für kausale Zusammenhänge ist die zeitliche Abfolge von der Ursache vor der Wirkung.
Grundproblem der Kausalanalyse
Kausale Zusammenhänge in ihrem etablierten Verständnis setzen die Annahme voraus, dass für jede Analyseeinheit mehrere potenzielle Ergebnisse möglich sind, je nach Ausprägung der kausalen Grösse oder des Treatments. Die Differenz zwischen den einzelnen Ergebnissen ist dann der kausale Effekt. Diese Situation ist jedoch kontrafaktisch, da zwei alternative Ereignisse für ein und dieselbe Einheit nicht existieren.
Die einzige verbleibende Untersuchungsmöglichkeit besteht darin, verschiedene Einheiten mit unterschiedlichen Treatment-Zuständen zu vergleichen. Das Problem besteht jedoch darin, dass diese Gruppen systematisch verschieden sein können, und zwar in Bezug auf die Faktoren, die für die Richtung oder Stärke des beobachteten Zusammenhangs relevant sein können. Ziel einer Kausalanalyse ist es, diese Verzerrung zu minimieren.
Zufallsexperimente
Einem klassischen Experiment liegt die Logik zugrunde, dass bei einer rein zufälligen Zuordnung der Untersuchungseinheiten in Gruppen ihre Eigenschaften – also auch die, die das Ergebnis verzerren könnten – gleich verteilt sind. Und zwar genauso wie in der Grundgesamtheit, aus der die Elemente gezogen wurden. Es gäbe also keine systematischen Unterschiede zwischen den Gruppen und man kann unterschiedliche Ergebnisse unbedenklich auf einen kausalen Effekt zurückführen.
Allerdings können bei der „zufälligen“ Zuweisung Fehler auftreten und es kommt auch häufig vor, dass die Stichproben nicht gross genug sind, um das Ergebnis auch inferenzstatistisch abzusichern. Das grösste Problem des experimentellen Designs besteht aber darin, dass es für viele, vor allem sozialwissenschaftliche Fragestellungen gar nicht durchführbar ist. Man würde z. B. niemandem verbieten, zur Schule zu gehen, um den genauen Effekt des Schulbesuchs zu untersuchen.
(Einige) nicht-experimentelle Methoden zur Schätzung kausaler Effekte
Standard-Regressionsverfahren
Entgegen einem weit verbreiteten Vorurteil kann eine „einfache“ Regression für Kausalanalysen verwendet werden. Denn durch eine geschickte Auswahl von Kontrollvariablen besteht die Möglichkeit, den theoretischen Kausalpfad zu separieren und zu testen. Komplexe Kausalzusammenhänge werden dann durch die Kombination mehrerer Regressionen, z. B. im Rahmen eines Strukturgleichungsmodells, abgebildet.
Dieser Ansatz funktioniert jedoch nur, wenn das Modell vollständig ist und alle potentiellen Störer tatsächlich und mit ausreichender Varianz gemessen wurden, was häufig nicht der Fall ist.
Propensity Score Matching
Dieses Verfahren versucht, die vorliegende Stichprobe in zwei möglichst identische Gruppen aufzuteilen, die sich nur in der Ausprägung des (vermutlich) kausalen Faktors unterscheiden. Der Unterschied im Ergebnis kann dann als kausaler Effekt interpretiert werden. In gewisser Weise wird damit versucht, ein experimentelles Design ex post zu replizieren. Das Matching erfolgt auf Basis der Ähnlichkeit in den relevanten Pre-Treatment-Variablen. Im Gegensatz zu einem reinen Zufallsexperiment müssen diese also bekannt und in den Daten enthalten sein.
Der Vorteil gegenüber einer Regression liegt darin, dass nicht bekannt sein muss, wie diese unabhängigen Variablen funktional mit der abhängigen Variable zusammenhängen. Der Nachteil besteht darin, dass Fälle, die keinen exakten „Zwilling“ haben, eliminiert werden, was oft zu grossen Fallzahlverlusten führt.
Fixed-Effects-Modelle
Die Idee dieses Modelltyps besteht darin, alle zeitkonstanten Unterschiede zwischen den Analyseeinheiten pauschal aus der Gleichung zu entfernen, statt potenzielle Störvariablen zu identifizieren und dafür zu kontrollieren. Dies geschieht, indem für jede Einheit eine Dummy-Variable in das Modell aufgenommen wird. Dies ist nur dann sinnvoll, wenn Paneldaten vorliegen, d. h. wenn es für jede Einheit auch mehrere Messungen gibt. Die abhängige Variable und die unabhängigen Variablen müssen im Zeitablauf unterschiedliche Werte annehmen können.
Difference-in-Differences (DiD)
Für DiD ist eine Messung vor und mindestens eine Messung nach Beginn des Treatments erforderlich. Zu diesem Zeitpunkt muss der Effekt bereits eingetreten sein. Man bildet für die Treatment- und Kontrollgruppe die Differenzen in der Ausprägung der abhängigen Variable nach und vor dem Treatment und anschliessend die Differenz dieser beiden Differenzen. Diese Differenz in Differenzen interpretiert man als den kausalen Effekt.
Der absolute Ausgangswert der abhängigen Variable (Baseline) und damit alle Merkmale, die ihn systematisch beeinflussen, werden damit irrelevant. Theoretisch können Störgrössen aber nicht nur die Baseline, sondern auch die Veränderung über die Zeit beeinflussen, was man dann fälschlicherweise als Teil des kausalen Effekts interpretieren würde. Dies soll bei der DiD ausgeschlossen werden können (Parallel Trend Assumption).
Regression Discontinuity Design (RDD)
Wenn keine Vergleichsgruppe, aber eine längere Messzeitreihe zur Verfügung steht, kann das RDD angewendet werden. Damit untersucht man die kausale Wirkung singulärer Ereignisse, indem man die Entwicklungen der abhängigen Variable vor und nach dem Ereignis statistisch vergleicht. Am häufigsten werden hierfür lineare Trends verwendet. Wenn ein kausaler Zusammenhang besteht, sollte ein signifikanter Unterschied vorliegen. Wichtig bei einer RDD ist die Bestimmung des korrekten funktionalen Zusammenhangs, dessen Diskontinuität untersucht wird. Das ist nicht immer trivial. Ausserdem muss ausgeschlossen werden, dass an der gleichen Schnittstelle alternative Ereignisse stattfanden, die den tatsächlichen Effekt verursacht haben.
Theoretische Vorarbeit
Kausalität bildet eigentlich eine theoretische Annahme und es gibt nicht die perfekte Methode, kausale Zusammenhänge per Design aufklärt. Vielmehr bedarf es eines klaren theoretischen Modells der kausalen Zusammenhänge und der möglichen systematischen Störbeziehungen. Erst dann wählt man ein empirisches Modell, das dem theoretischen möglichst nahekommt.
Dabei geht es nicht (nur) um abstraktes Theoretisieren, auch formale theoretische Modelle gewinnen zunehmend an Bedeutung. Eine Möglichkeit ist z. B. die Erstellung von Pfaddiagrammen nach bestimmten Regeln, sogenannte Directed Acyclic Graphs (DAGs). Damit können potenzielle Fehler in der kausalen Modellierung bereits in der Planungsphase erkannt werden.
Hier drei einfache klassische Beispiele:
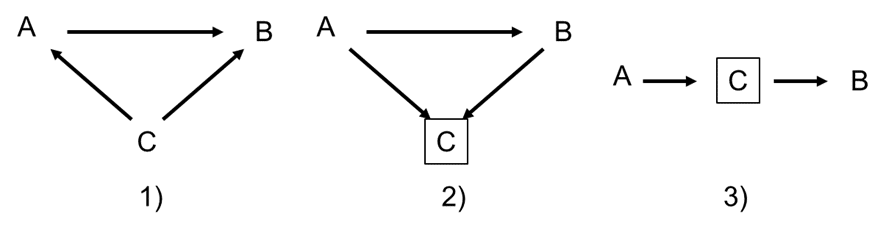
- Scheinkorrelation: kein kausaler Zusammenhang zwischen A und B, aber eine Korrelation, wenn C nicht kontrolliert wird
- Endogenous selection bias: kein kausaler Zusammenhang zwischen A und B, aber eine Korrelation, wenn C kontrolliert wird
- Mediation: ein kausaler Zusammenhang zwischen A und B, C ist der Mechanismus (der Mediator); keine Korrelation, wenn C kontrolliert wird
Fazit
Die Analyse von kausalen Zusammenhängen erfordert eine solide theoretische Vorbereitung sowie die richtige Wahl des Forschungsdesigns und der statistischen Methoden. Datenverfügbarkeit und -qualität spielen ebenfalls eine wichtige Rolle. Das häufig verwendete Schlagwort „Kausalanalysen“ darf nicht darüber hinwegtäuschen, dass es keine Anwendung gibt, die ohne Annahmen und Voraussetzungen Kausalitäten aufklärt. Die gute Nachricht ist, dass es mittlerweile eine grosse Palette an geeigneten Verfahren gibt. Sie sollten dabei der Forschungsfrage und Datenlage angemessen ausgewählt werden.
Und wenn Sie professionelle Hilfe bei der Aufstellung eines theoretischen Modells und der der Auswahl einer geeigneten statistischen Methode benötigen, wenden Sie sich an Sie unsere Statistik Beratung!
Weiterführende Literatur
Elwert, Felix; Winship, Christopher (2014): Endogenous selection bias. The problem of conditioning on a collider variable. In: Annual Review of Sociology 40, S. 31–53. https://www.annualreviews.org/content/journals/10.1146/annurev-soc-071913-043455
Legewie, Joscha (2012): Die Schätzung von kausalen Effekten. Überlegungen zu Methoden der Kausalanalyse anhand von Kontexteffekten in der Schule. In: Kölner Zeitschrift für Soziologie und Sozialpsychologie 64 (1), 123–153. https://link.springer.com/article/10.1007/s11577-012-0158-5