Eine Korrelationsanalyse ist ein beliebtes Mittel, um den Zusammenhang zwischen zwei Variablen zu untersuchen. In vielen Fällen können beobachtete Korrelationen jedoch durch Störvariablen beeinflusst werden. So entstehen häufig Scheinkorrelationen, gelegentlich kann aber auch ein bestehender Zusammenhang durch Störgrößen verdeckt werden. Wenn man den Einfluss von Störvariablen vermutet, kann man die partielle Korrelation (auch Partialkorrelation) berechnen, um bekannte Kontrollvariablen zu eliminieren. In diesem Artikel stellen wir daher die partielle Korrelation kurz vor und zeigen, wo diese sinnvoll eingesetzt werden kann.
Wenn Sie Unterstützung bei der Auswertung oder Interpretation Ihrer Daten benötigen, helfen unsere Statistiker Ihnen gerne weiter. Kontaktieren Sie uns für eine kostenlose Beratung & ein unverbindliches Angebot.
Dieser Artikel beantwortet folgender Fragen
- Was ist der partielle Korrelationskoeffizient?
- Wie wird der partielle Korrelationskoeffizient berechnet?
- Wie kann ich den partiellen Korrelationskoeffizienten interpretieren?
Wann wird die partielle Korrelation eingesetzt?
Möchte man den linearen Zusammenhang zwischen zwei Variablen (z.B. Rauchen und Blutdruck) untersuchen, wird häufig zunächst eine einfache Korrelationsanalyse herangezogen. Ein hierbei gefundener signifikanter Zusammenhang lässt jedoch nicht zwingend auf Kausalität schließen (z.B. bei Störchen und Babys). Im Allgemeinen dürfen wir davon ausgehen, dass jede Korrelation zwischen zwei Variablen von weiteren Variablen mitbestimmt wird.
Erhalten wir also eine signifikante Korrelation ohne kausalen Zusammenhang, liegt eine Scheinkorrelation vor. Mit hoher Wahrscheinlichkeit besteht die Korrelation nur durch eine dritte Variable, die sogenannte Kontrollvariable oder auch Störgröße. Umgekehrt kann eine solche Störgröße auch dazu führen, dass ein eigentlich bestehender Zusammenhang verdeckt wird. In beiden Fällen kommt die Partialkorrelation zum Einsatz. Mit Ihrer Hilfe kann die Kontrollvariable / Störgröße identifiziert und eliminiert werden. Als Ergebnis erhalten wir den eigentlich bestehenden Zusammenhang, der sich dann entweder als nicht vorhanden entpuppt oder deutlich stärker hervortritt.
Wünschen Sie ein maßgeschneidertes und individuelles Coaching zum Verständnis und Anwendung statistischer Verfahren? Oder Sie benötigen Hilfe bei der Auswertung und Interpretation Ihrer Daten? Von der Statistik Nachhilfe bis hin zur Unterstützung durch eine vollständige statistische Auswertung: Unsere Experten helfen Ihnen schnell und kompetent weiter!
Partielle Korrelation in der Praxis: Warum der Storch nicht die Babys bringt
Das wohl bekannteste Beispiel aus der Anwendung der partiellen Korrelation ist eine Studie, in welcher der Zusammenhang zwischen der menschlichen Geburtenrate und der Zahl der Storchenpaare untersucht wurde. Hier fand man eine signifikant positive Korrelation zwischen der Zahl der Geburten und der Zahl der Storchenpaare. In Regionen mit mehr Störchen gibt es also auch mehr Babys. Bringt der Storch nun also die Kinder? Natürlich nicht! Korrelation bedeutet noch nicht Kausalität. Da hier offensichtlich kein kausaler Zusammenhang bestehen kann, wird mit Hilfe der partiellen Korrelation die Störgröße oder auch Kontrollvariable gesucht und eliminiert. Tatsächlich ist die hier aufgedeckt Scheinkorrelation ein Resultat der Industrialisierung und Verstädterung und der damit verbundenen Ortswahl: in ländlichen Gegenden sind die Lebensbedingungen sowohl für Familien als auch für Störche besser. Es gibt auf dem Land somit aus demselben Grund mehr Familien mit Kindern und auch mehr Störche als in städtischen industrialisierten Ballungszentren.
Partielle Korrelation in klinischen Studien
Auch bei der statistischen Analyse von Ergebnissen aus klinischen Studien ist die Partialkorrelation ein wichtiges Werkzeug. Hier werden neben den zu untersuchenden Parametern häufig zusätzlich diverse demografische Variablen (Alter, Geschlecht, etc.) festgehalten.
Es konnte beispielsweise festgestellt werden, dass eine Reihe von äußerlich sichtbaren Gefäßveränderungen wie Krampfadern, Hämorrhoiden, kutane Venenerweiterungen usw. signifikant miteinander korreliert auftreten und sich als Ausdruck einer möglichen „allgemeinen vererbten Venenwanddysplasie“ manifestieren könnten. Alle im sogenannten „Status varicosus“ zusammengefassten Veränderungen treten mit zunehmendem Alter häufiger auf. Mit Hilfe der partiellen Korrelation konnte der Einfluss des Alters ausgeschaltet werden und es stellte sich heraus, dass es keinen engeren Zusammenhang zwischen den einzelnen Merkmalen gibt und jedes Merkmal für sich letztlich allein mit dem Alter zusammenhängt.
Andererseits kann ein Zusammenhang aber erst durch die Ausschaltung des Einflusses einer Störgröße sichtbar werden.
Im Allgemeinen ermöglich die Berechnung des partiellen Korrelationskoeffizienten, Störungen durch diejenigen Faktoren auszuschalten, welche im Versuch nur schlecht oder überhaupt nicht kontrolliert werden können. Störvariablen werden auch als konfundierende Variablen (engl. Confounder) bezeichnet. Eine Störung durch diese bezeichnet man als Konfundierung.
Berechnung partieller Korrelationskoeffizient
Um nun zu untersuchen, ob eine bereits gefundene statistisch signifikante Korrelation den eigentlichen Zusammenhang darstellt oder aber durch eine weitere Variable kontrolliert wird, berechnen wir den partiellen Korrelationskoeffizienten. Anders gesagt berechnen wir die Korrelation zwischen zwei Variablen x und y unter Ausschluss einer dritten Variablen z.
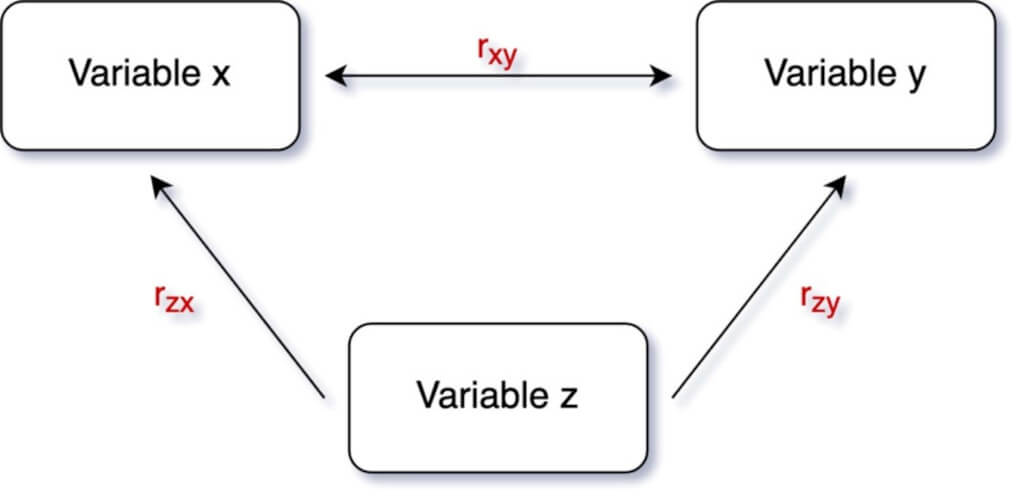
Wenn für drei Variablen x, y und z lineare Korrelationen vorliegen und rxy, rxz und ryzdie paarweise berechneten Korrelationskoeffizienten sind, wird der partielle Korrelationskoeffizient zwischen x und y unter Ausschluss von z wie folgt berechnet:
\(r_{xy,z}=\frac{r_{xy}-r_{xy}\cdot r_{yz}}{\sqrt{\left ( 1-r_{xz}^{2} \right )\cdot\left ( 1-r_{yz}^{2} \right )}}\)Der so berechnete partielle Korrelationskoeffizient erklärt also den Zusammenhang zwischen einer abhängigen und einer unabhängigen Variablen unter Ausschluss des Einflusses einer weiteren Einflussgröße.
Von partieller Korrelation 2. Ordnung spricht man, wenn statt einer Kontrollvariable zwei Kontrollvariablen berücksichtigt werden und der partielle Korrelationskoeffizient unter Ausschluss dieser beider berechnet wird.
Interpretation partieller Korrelationskoeffizient
Für die Interpretation wird der ursprüngliche (zweidimensionale) Korrelationskoeffizient zwischen x und y mit dem partiellen Korrelationskoeffizienten rxy.z verglichen. Die nachfolgende Schreibweise als Betrag berücksichtigt sowohl den positiven als auch den negativen Fall.
Wir erhalten folgende vier Fälle:
| |rxy.z|< |rxy| | Die partielle Korrelation ist kleiner als die ursprüngliche Korrelation. Die Korrelation rxy wurde aufgrund des Einflusses von z ursprünglich überschätzt. Im Extremfall erreicht rxy.z den Wert 0, d.h. die Partialkorrelation zeigt keinen Zusammenhang. Dann wurde eine Scheinkorrelation aufgedeckt. |
| |rxy.z|> |rxy| | Die partielle Korrelation ist größer als die ursprüngliche Korrelation. Die Korrelation rxy wurde aufgrund des Einflusses von z ursprünglich unterschätzt. Der partielle Korrelationskoeffizient ist hier besser geeignet, um den tatsächlichen Zusammenhang zu beschreiben. |
| |rxy.z|» |rxy| | Die partielle Korrelation hat in etwa den gleichen Wert wie die ursprüngliche Korrelation. Es liegt somit keine Störung durch z vor. Der einfache Korrelationskoeffizient rxy beschreibt den Zusammenhang hinreichend. |
| |rxy.z|und |rxy| sind beide signifikant | Sowohl der partielle Korrelationskoeffizient als auch der einfache Korrelationskoeffizient sind beide signifikant aber haben unterschiedliche Werte. In diesem Fall liegt nur eine geringe oder keine Störung vor. Die Variable z stellt somit einen zusätzlichen Einflussfaktor dar. Für diesen Fall kann eine multiple Korrelationsanalyse unter Einbezug von z als dritte Variable in Betracht gezogen werden. |
Störche bringen doch keine Babys
Betrachten wir dazu nochmals unser obiges Beispiel zur Analyse des Zusammenhangs zwischen Störchen und Babys. Hier wird für den partiellen Korrelationskoeffizienten ein Wert von p=0.08 berechnet. Er ist somit nicht nur deutlich kleiner als der ursprüngliche einfache Korrelationskoeffizient, sondern auch nicht signifikant und nahe Null. Hier liegt also eine eindeutige Scheinkorrelation (Fall 1: |rxy.z|< |rxy|) vor.
Einen Zusammenhang hätten wir nur dann annehmen dürfen, wenn die einfache Korrelation signifikant und größer oder gleich dem partiellen Korrelationskoeffizienten gewesen wäre. Dies ist jedoch nicht der Fall und deckt sich mit unserem Wissen, dass Störche keine Babys bringen.
Fazit
Wie wir in diesem Artikel zeigen konnten, bedeutet Korrelation nicht immer gleich Kausalität. Sind uns mögliche Störgrößen oder zusätzliche Kontrollvariablen bekannt, so kann es sich lohnen, eine Partialkorrelation zu berechnen. Scheinkorrelationen wie etwa zwischen Störchen und Babys werden damit schnell aufgedeckt.
Weiterführende Quellen
Sachs, L., Hedderich, J: Angewandte Statistik – Methodensammlung mit R.
Wagner, G: Zur Methodik des Vergleichs altersabhängiger Dermatosen. (Zeitschr. menschl. Vererb. – Konstit.-Lehre)
Lehrmaterial der Uni Ruhr-Bochum zur partiellen Korrelation (pdf-Datei)