Den Mittelwert – auch arithmetisches Mittel – kennt eigentlich jeder. Doch wann genau ist der Mittelwert eigentlich die richtige Wahl und was sind bessere Alternativen?
Gefährlicher Nachteil beim Mittelwert berechnen
Den Mittelwert zu berechnen stellt meistens kein besonderes Problem dar, jedoch muss bei der Interpretation darauf geachtet werden, dass der klassische Mittelwert auch wirklich die richtige Wahl für die Daten war. Besonders kritisch ist die Interpretation, wenn sich entweder viele oder einige sehr extreme Ausreisser im Datensatz befinden. Ausreisser sind Datenpunkte, die sehr weit über oder unter den anderen Datenpunkten liegen. Wir möchten Ihnen zeigen, wie Sie eine solche Fehlinterpretation vermeiden und stattdessen bessere Kennzahlen berechnen.
Im Folgenden Beispiel treffen sich fünf ehemalige Schulkameraden wieder und vergleichen ihr jährliches Nettoeinkommen.
| Alex | Sebastian | Jan | Philipp | Frederik |
| 32.000€ | 39.000€ | 44.000€ | 49.000€ | 350.000€ |
Berechnet man für die Fünf nun das durchschnittliche Einkommen kommt man auf 102.400€. Man sieht schnell, dass dieser Wert nicht wirklich repräsentativ dafür ist, was die fünf tatsächlich verdienen, da Frederik den Durchschnitt stark nach oben zieht.
Doch was tun, wenn man mit einem ähnlichen Datensatz konfrontiert wird? Es gibt drei Möglichkeiten grobe Fehler bei der Interpretation zu vermeiden.
In unserem Beispiel sieht das so aus: Einerseits könnte man das Gehalt von Frederik ausschliessen und das durchschnittliche Gehalt der anderen Vier berechnen. Stellt man sich aber nun vor, dass man mit einem grösseren Datensatz zum Einkommen arbeitet, würde dies bedeuten, das Sample nur für die Berechnung des Mittelwertes zu verändern. Das sollte man aber auf gar keinen Fall tun, da die gesamte Analyse mit demselben Sample stattfinden muss, um die Ergebnisse später angemessen interpretieren zu können. Entfernt man den Wert vollständig aus dem Sample, würden auch alle anderen Beobachtungen zu dieser Person verloren gehen und der Datensatz würde schrumpfen.
Die zweite Lösung wäre, eine Kategorie zu bilden. Zum Beispiel „mehr als 50.000€“. Das ist allerdings mit einem Informationsverlust verbunden, den man auch unbedingt vermeiden sollte.
Median berechnen, so wird’s gemacht – Die sinnvolle Alternative zum Mittelwert
Die dritte und beste Lösung wäre hier, den Median zu berechnen. Der Median ist der mittlere Wert aller Daten und teilt den Datensatz genau in der Hälfte. In unserem Beispiel gibt es fünf Werte – also ist der dritte der Median. Wichtig ist hierbei, dass die Werte der Grösse nach sortiert sein müssen. In unserem Beispiel liegt der Median also bei 44.000€. Diese Kennzahl trifft die Eigenschaften des Datensatzes wesentlich genauer und könnte korrekt interpretiert werden.
Insgesamt bietet sich eine Verwendung des Medians vor allem dann an, wenn es sich um eine sehr schiefe Verteilung handelt. Das wäre bei Daten mit wenigen Fällen zu grossem Einkommen aber vielen Fällen mit geringem Einkommen gegeben.
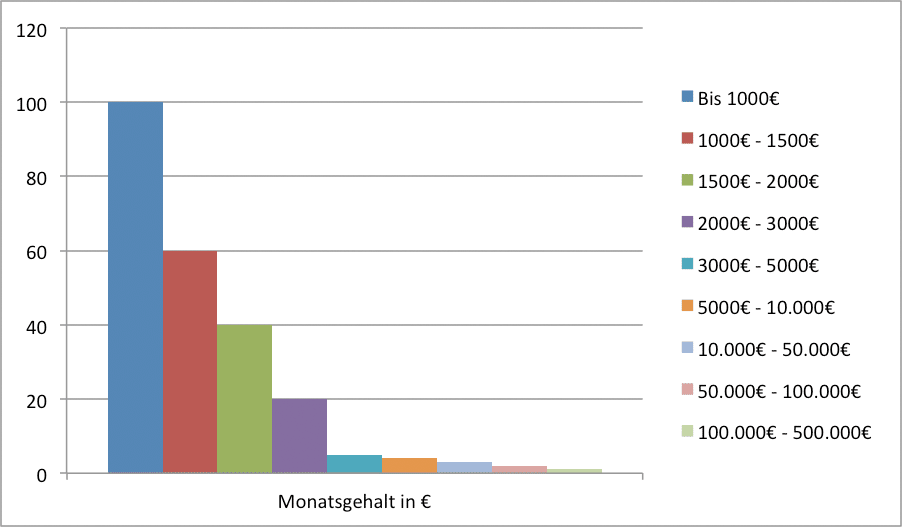
In diesem Beispiel mit 235 Fällen würde das mittlere Monatsgehalt bei 6466,17€ liegen. Ein Wert, der von der grössten Zahl der Fälle im Datensatz nicht ansatzweise erreicht wird.
Der Median hingegen wäre der 118. Fall. Dieser liegt in der zweiten Kategorie (1000€ – 1500€) ist somit 1250€. Das trifft die Eigenschaft der schiefen Verteilung wesentlich besser als das arithmetische Mittel.
Eine zweite Art von Daten, bei denen der Median sich besonders gut einsetzen lässt, sind sogenannte zensierte Daten. Es könnte zum Beispiel betrachtet werden, ob Personen nach ihrem Studienabschluss einer bestimmten Fachrichtung innerhalb von 18 Monaten auf ein Jahresgehalt von mindestens 30.000€ kommen oder nicht. Hier erhält man für die Personen, die das Ziel nicht erreichen den Wert „mehr als 18 Monate“, woraus sich kein Mittelwert berechnen lässt. Liegen allerdings mindestens die Hälfte der Beobachtungen unter dem Wert von 18 Monaten, lässt sich der Median als sinnvolle Kennzahl angeben.
Neben der Unempfindlichkeit Ausreissern gegenüber lässt sich der Median ausserdem auch auf ordinalskalierte Daten anwenden. Typisch dafür sind Angaben über die Produktzufriedenheit von „sehr unzufrieden“, „eher unzufrieden“, „eher zufrieden“ bis „sehr zufrieden“. Zwar ist hier noch eine Umwandlung in eine Skala von 1 – 4 möglich, um einen Mittelwert zu berechnen, jedoch funktioniert dies nicht immer.
Überprüft man zum Beispiel den Dienstrang beim Militär („General“, „Major“, „Leutnant“, „Feldwebel“, „Unteroffizier“, „Gefreiter“), würde eine Umwandlung in eine Skala nicht unbedingt sinnvoll sein, der Median liesse sich im Gegensatz zum Durchschnitt dennoch berechnen.
Modus – nur so lässt sich mit Nominalskalen arbeiten
Der letzte Teil in der Trias der Kennzahlen ist der Modus (Modalwert). Der Modus ist die am häufigsten auftretende Ausprägung einer Variable in einem Datensatz. Er sollte im Allgemeinen nicht dem arithmetischen Mittel oder Median zur Interpretation vorgezogen werden, da der Informationsgehalt oft eher gering ist. Allerdings ist der Modus die einzige Kennzahl, die sich für nominalskalierte Daten sinnvoll berechnen lässt. Möchte man zum Beispiel wissen, welche Produktfarbe bei den Kunden am besten ankommt, so ist der Modus die entscheidende Kennzahl, die diese Information liefern kann.
Es ist jedoch auch beim Umgang mit dem Modus Vorsicht geboten. In sogenannten bimodalen oder multimodalen Verteilungen kann es vorkommen, dass der Modus nicht eindeutig ist. Es kann sein das die gleiche Zahl an Kunden die grüne und blaue Ausführung des Produkts am besten findet.
Generell gilt: Am besten mit einem geeigneten Programm alle drei berechnen und überprüfen, wo eine Interpretation am besten möglich ist. Dafür reicht eine einfache Software zur Tabellenkalkulation schon aus.