Die Herstellung kostengünstiger, sicherer und qualitätskonformer Produkte ist für industrielle Unternehmen zweifelsohne entscheidend. Die Grundlage hierzu ist ein fundamentales Verständnis von Produkt und Prozessen unverzichtbar. Diese Kenntnisse werden in der Regel durch komplexe multivariate mathematische Modelle beschrieben, die ihrerseits wiederum aus empirisch erhobenen Daten abgeleitet werden. Die statistische Versuchsplanung (Design of Experiments im englischen – DoE) bietet hierzu eine Sammlung effizienter und effektiver Methoden aus dem Bereich des Quality Engineering. Diese Methoden erlauben die Daten möglichst systematisch und modellorientiert zu erheben.
Möchten Sie bei Ihrer Versuchsplanung von unserer professionellen Unterstützung profitieren? Informieren Sie sich gern über unsere Dienstleistungen für die statistische Versuchsplanung.
Google Rating
-
Ich habe ausschließlich positive Erfahrungen mit Novustat gemacht. Angefangen mit einer freundlichen Erstberatung erfolgte … Mehr im gesamten Prozess eine kompetente Betreuung meines Anliegens. Selbst auf kurzfristige Änderungen wurde schnell reagiert. Generell ist die Erreichbarkeit besonders hervorzuheben, da mein Ansprechpartner teilweise wenige Minuten nach Kontaktaufnahme auf meine Fragen geantwortet hat. Das Projekt konnte zu meiner vollen Zufriedenheit abgeschlossen werden. Dementsprechend ist Novustat eine klare Empfehlung meinerseits!
-
Meine Auswertungsdaten habe ich recht spontan erhalten und bin umso dankbarer, dass die Novustat Statistik-Beratung so kurzfristig … Mehr übernommen hat! Alle meine Zusatzfragen und -analysen wurden zu meiner Zufriedenheit geklärt und auch für Nachfragen & Erklärungen wurde sich viel Zeit genommen. So ist für mich alles verständlich und nachvollziehbar und ich bin sehr dankbar für ihre Flexibilität und Auswertung!
-
Wirklich schnelle und professionelle Hilfe. Sofort nach Anfrage wurde mir weitergeholfen, sodass keine Zeit verloren ging … Mehr und ich konnte mich jederzeit mit Fragen an meinen Bearbeiter wenden und kurzfristig Gesprächstermine ausmachen. Sehr zu empfehlen!
Dieser Artikel über statistische Versuchsplanung (DOE) beantwortet folgende Fragen
- Was ist statistische Versuchsplanung (Design of Experiments – DoE)?
- Welche Ziele verfolgt statistische Versuchsplanung
- Warum ist statistische Versuchsplanung so wichtig?
- Welche Phasen und Ansätze zur statistischen Versuchsplanung gibt es?
- Wie werden Daten aus Versuchsplanungsprojekten ausgewertet?
Was ist statistische Versuchsplanung (Design of Experiments – DoE)?
Im Rahmen eines „Quality-by-Design“ Ansatzes zur Qualitätsoptimierung spielt die statistische Versuchsplanung (DOE) eine besondere Rolle. Die systematische statistische Sammlung von Prinzipien und Methoden kann hier dazu dienen:
- Alle qualitätskritischen Parameter für Produkte und Prozesse zu identifizieren
- Die Einstellungen von Produkt- und Prozessparametern zu optimieren
- Grenzwerte und Spezifikationen der Parameter zu überprüfen
- Ein geeignetes „Prozessfenster“ („Design Space“) zu definieren, der ein annehmbares Qualitätsniveau sicherstellt
Gerne helfen wir Ihnen, einen statistischen Versuchsplan (DOE) professionell zu erstellen und zeitnah, verständlich, und kundenorientiert zu präsentieren. Nehmen Sie hierzu Kontakt mit uns auf für eine unverbindliche Erstberatung!
Hierzu wählt man meistens mögliche experimentelle Bedingungen aus einer Menge von unzähligen theoretisch möglichen Experimenten („Candidate Set“). Die ausgewählten experimentellen Bedingungen verwendet man dann zur empirischen Ermittlung mathematischer Optimierungsmodelle ausgewählt.
Diese Modelle können dann dazu genutzt werden, um komplexe Abhängigkeiten zwischen Produkt- und Prozessparameter einerseits und definierten Qualitätsparametern andererseits zu analysieren. Schließlich ist es mit diesen Modellen möglich die Qualität der Prozesse und Produkte systematisch und strukturiert zu optimieren.
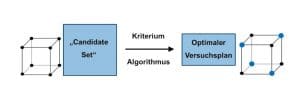
Durch diese systematischen Ansätze kann sichergestellt werden, dass die durchgeführten Experimente die maximalen Informationen zur Qualitätsoptimierung enthalten.
Welche Ziele verfolgt die statistische Versuchsplanung
Bei den meisten industriellen Anwendungen von statistischer Versuchsplanung ist die Verbesserung der Qualität das oberste Ziel. Diese Qualität lässt sich üblicherweise anhand von mehreren Qualitätsmerkmalen beschreiben. Qualitätsmerkmale können dabei allgemein von drei verschiedenen Parametertypen beeinflusst werden:
- Variablen, bei denen der Einfluss auf die Qualität und auch die optimalen Einstellungen bekannt sind.
- Störparameter („Noise“ – „Rauschen“), die entweder nicht kontrolliert werden können oder, beispielsweise aus Kostengründen, nicht kontrolliert werden sollen.
- Faktoren, bei denen der Einfluss auf die Produktqualität noch nicht bekannt ist. Diese Parameter werden üblicherweise in Versuchsplanungsstudien untersucht, während die Variablen auf der optimierten Einstellung konstant gehalten werden und es versucht wird, den Einfluss der Störparameter möglichst zu minimieren.
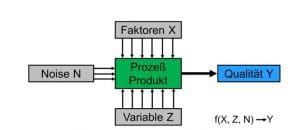
Eine Qualitätsoptimierung kann über die mathematische Funktionen f geschehen, die den Zusammenhang der Parametertypen – Variable, Noise und Faktoren – und der Qualität beschreiben und modellieren. Durch Schätzung der unbekannten Modellparameter kann der Einfluss der Parameter auf die Qualität quantifiziert werden, was es dann ermöglicht Einstellungen zu finden, die reproduzierbar zu akzeptabler, optimaler Qualität führen.
In diesem Zusammenhang können die Zielsetzungen der statistischen Versuchsplanung folgendermaßen formuliert werden:
- Identifizierung relevanter Parameter zur Optimierung der Produktqualität
- Robustheit von Prozess und Produkt
- Bestimmung optimaler Prozessfenster
- Qualitätsoptimierung im Sinne von
- Maximierung der Ausbeute
- Minimierung der Variabilität
- Maximierung der Zuverlässigkeit
Statistische Versuchsplanung: Welchen Versuchsplan soll ich wählen?
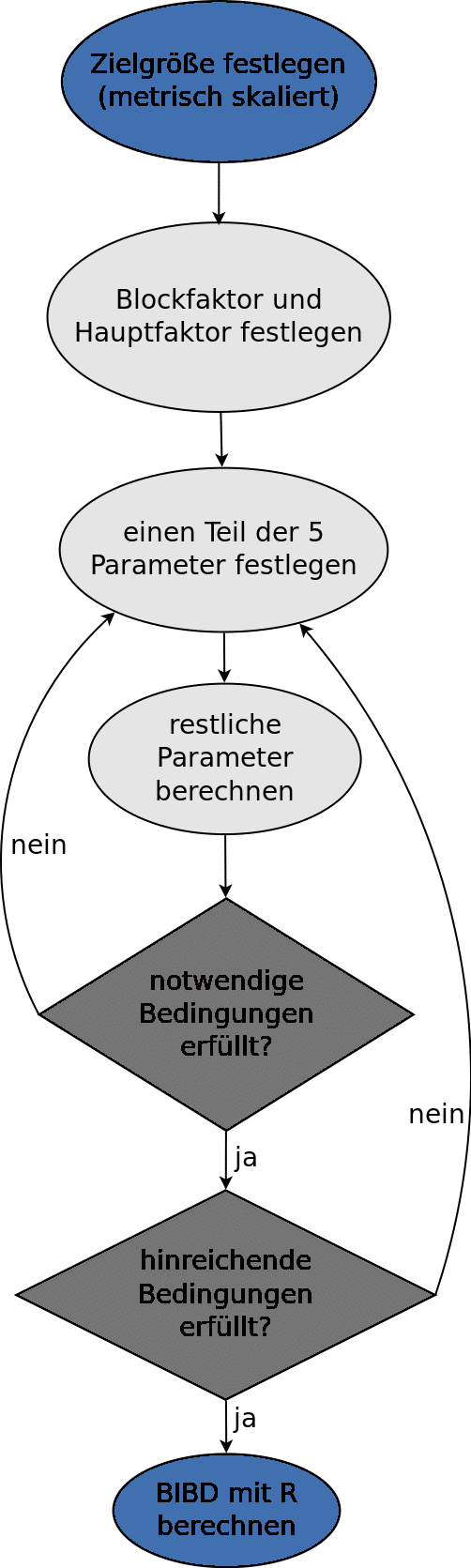
Die Vielzahl statistischer Versuchspläne lässt sich grob in zwei Kategorien gliedern, vollständige und unvollständige Versuchspläne. Möchten Sie alle Kombinationen an Faktorstufen in Ihrem Experiment testen, führen Sie einen vollständigen Versuchsplan durch. Bei einem Faktor A mit den fünf Stufen a1, a2, a3, a4 und a5 sind also fünf Einzelversuche durchzuführen. Kommt nun ein weiterer Faktor B mit den fünf Stufen b1, b2, b3, b4 und b5 hinzu, werden alle Stufen des Faktors A mit allen Stufen des Faktors B kombiniert. Die Versuchsplanung enthält also die 5*5 = 25 Kombinationen (a1,b1), (a1,b2), (a1,b3) und so weiter an Faktorstufen. Durch die Hinzunahme eines weiteren Faktors C mit fünf Stufen muss man sogar insgesamt 5*5*5 = 125 Einzelversuche durchführen. Möchten Sie einen vollständigen Versuchsplan erstellen, müssen Sie also berücksichtigen, dass der Stichprobenumfang exponentiell anwächst – und zwar mit jedem zusätzlichen Faktor und jeder zusätzlichen Faktorstufe. Das ist aus finanziellen und zeitlichen Gründen oftmals nicht durchführbar. Doch zum Glück bietet die Versuchsplanung eine Alternative zur Verfügung – den unvollständigen Versuchsplan. Beim unvollständigen Versuchsplan wird die große Anzahl an Faktorstufenkombinationen systematisch reduziert und zwar ohne dass es zu verzerrten Schätzungen der Effekte oder anderen Nachteilen kommt. Ein besonderer unvollständiger Versuchsplan ist der balancierte unvollständige Versuchsplan (englisch: BIBD = Balanced Incomplete Block Design), welcher neben einem Blockfaktor einen weiteren (den interessierenden) Faktor beinhaltet.
Phasen statistischer Versuchsplanung zur Prozess- und Produktoptimierung
Idealerweise werden Versuchsplanungsstudien zur Qualitätsverbesserung in drei aufeinander folgenden Phasen durchgeführt:
- In einer ersten „Screening“- Phase werden zuerst relevante Faktoren zur Qualitätsverbesserung aus einer Vielzahl von infrage kommenden Faktoren identifiziert. Diese Phase bildet somit die Basis für das Prozessverständnis und die weiteren experimentellen Studienphasen.
- In der sich anschließenden Optimierungsphase werden nun die zu optimaler Produktqualität führenden Einstellungen der vorher identifizierten, relevanten Faktoren bestimmt.
- Über Sensitivität bzw. Toleranzversuchspläne wird in einer letzten Phase ein geeignetes Prozessfenster für die zu optimaler Einstellungen der qualitätsrelevanten Faktoren bestimmt. Wenn sich die Einstellungen der Faktoren in diesem Bereich bewegen, kann von konstanter, akzeptabler Produktqualität ausgegangen werden.
Ansätze und Vorteile statistischer Versuchsplanung
Ganz allgemein können bei der Beschreibung und Analyse des Zusammenhangs von Parametern und Qualität verschiedene nicht-statistische und statistische Methoden zum Einsatz kommen:
„Versuch-und-Irrtum“: keine zuverlässige Planung möglich
Beim so-genannten „Versuch-und-Irrtum“ Ansatz („Trial-and-Error“ / „Spray&Pray“ / „Bulls-Eye Approach“) werden die Einstellungen der untersuchten Faktoren in unsystematischer Weise verändert. Klarer Nachteil dieser Vorgehensweise ist, dass hierdurch eine mathematische Modellierung erschwert wird. Weiterhin ist eine zuverlässige Planung von Ressourcen fast unmöglich. Im Extremfall kann zwar eine Qualitätsverbesserung erzielt werden, es bleibt aber unklar auf welchen Faktor die Qualität zurückzuführen ist.
„One-Factor-At-a-Time“ (OFAT): in der Praxis gebräuchlich, aber nicht unproblematisch
Der „One-Factor-At-a-Time“ (OFAT) Ansatz ist in der Praxis zur Versuchsplanung sehr gebräuchlich. Hierzu variiert man die Einstellungen der einzelnen Faktoren nacheinander, während die übrigen Faktoren konstant bleiben. Bei dieser Methodik ist eine a-priori Planung der benötigten Ressourcen möglich. Falls zwischen den untersuchten Faktoren keine (starken) Wechselwirkungen existieren, liefern diese Prozeduren auch zuverlässige Optimierungsergebnisse. Problematisch ist dieser Ansatz allerdings bei Wechselwirkungen. Der Einfluss eines Faktors ist dann abhängig von der Einstellung eines zweiten Faktors. In dem Fall kann dieser Ansatz deshalb zu Ergebnissen führen, die abhängig von der Versuchsreihenfolge sind.
Vollfaktorieller statistischer Versuchsplan: Theoretisch ideal, praktisch schwer umzusetzen
Der aus statistischer Sicht ideale Versuchsaufbau ist ein vollfaktorieller Versuchsplan. Bei diesem werden alle möglichen Faktoreinstellungen experimentell untersucht. Dieses Vorgehen ermöglicht die Analyse aller Faktoreinflüsse. Dies umfasst auch höhere Wechselwirkungen, welche mehr als zwei Faktoren beinhalten. Allerdings erfordern voll-faktorielle Versuchspläne unter Umständen extrem hohe Versuchsanzahlen. Bei drei zu untersuchenden Faktoren mit jeweils fünf Einstellmöglichkeiten wären beispielsweise bereits 53 = 125 individuelle Experimente notwendig. Deshalb ist der vollfaktorielle Ansatz für die industrielle Praxis nur bedingt anwendbar.
Statistische Versuchsplanung (DOE): nur die informativsten Experimente
Als Ausweg bieten sich Verfahren der statistischen Versuchsplanung an, die es ermöglichen, die Anzahl der Experimente zu reduzieren. Ganz allgemein handelt es sich dabei um Verfahren, die unter definierten Annahmen die „informativsten“ Experimente aus dem theoretisch möglichen voll-faktoriellem Versuchsplan auswählen.
Im Vergleich zu anderen unstrukturierten und unsystematischen Ansätzen zur Qualitätsoptimierung bieten die Methoden der statistischen Versuchsplanung für das Quality Engineering daher einige eindeutige Vorteile:
- Sie bilden die Basis für eine effiziente und effektive Qualitätsoptimierung
- Sie ermöglichen ein fundamentales Prozess- und Produktverständnis bei reduziertem Versuchsumfang
- Durch eine systematische und strukturierte Qualitätsoptimierung sind sie eine zuverlässige Basis für nachfolgende Optimierungsansätze
- Sie ermöglichen eine zuverlässige Planung von Ressourcen, Zeiten und Kosten
Erstellung eines geeigneten statistischen Versuchsplans
Wie in allen Bereichen der angewandten Statistik gibt es auch in der statistischen Versuchsplanung keinen „Overall-Best“ oder „One-Fits-All“ Ansatz. Kein Ansatz ist also für alle praktischen Situationen gleichmäßig gut geeignet. Vielmehr ist die Auswahl eines optimalen Versuchsplanes für eine konkrete Fragestellung von vielen Randbedingungen abhängig, wie:
- Zielsetzung des Projekts
- Modellkomplexität
- Versuchsraumeinschränkungen
- Ökonomische Restriktionen
Hierzu werden von der statistischen Theorie verschieden Typen von Versuchsplänen, die sich sowohl in ihrer Komplexität als auch in ihren mathematischen Voraussetzungen und Eigenschaften teilweise stark unterscheiden:
- Voll-faktorielle, teil-faktorielle oder Plackett-Burman Designs dienen in der Screening-Phase hauptsächlich zur (statistischen) Identifizierung von relevanten Faktoren.
- So-genannte Response-Surface-Method Designs oder Box-Behnken Designs kommen in der Optimierungsphase zum Einsatz, um die zur Qualitätsoptimierung führenden Faktoreinstellungen zu bestimmen.
- Für komplexere Fragestellungen sind optimale Designs geeignet. Denn diese Designs sind durch ihre algorithmische Konstruktion für nahezu alle praktischen Situationen – Versuchsraumeinschränkungen, spezielle Modellwahl, usw. – anwendbar.
- Im Gegensatz zu den bisher aufgeführten Versuchsplänen, die zu Konstruktion und Datenauswertung ein definiertes mathematisches Modell annehmen, bieten „Space-Filling“ Versuchspläne eine nichtparametrische Alternative. Durch diese Eigenschaft sind derartige Versuchspläne in der Praxis universell einsetzbar.
Datenauswertung: Von Beobachtungen über das Modell zur bestmöglichen Qualität
Ähnlich zur Konstruktion von geeigneten statistischen Versuchsplänen ist auch die verwendete Analysestrategie von einer Reihe Randbedingungen abhängig. Für die meisten Datenanalysen bilden dabei statistische Prozeduren aus den Bereichen die Grundlage:
- Multivariate, multiple, lineare und nicht-lineare Regression
- Loglineare und logistische Modelle für kategoriale Qualitätsmerkmale
- (Multivariate) ANOVA
- (Multivariate) ANCOVA
- Optimierungsalgorithmen
Als Besonderheiten statistischer Datenanalysen im Bereich der Versuchsplanung können darüber hinaus genannt werden:
- Spezielle grafische Analysen, oftmals in Form so-genannter Response-Surface-Method Plots, die Qualität in Abhängigkeit von Prozessparametern auf Basis eines quadratischen Regressionsmodells darstellen.
- Multiresponse Optimierung, die es ermöglicht simultan mehrere relevante und in der Regel voneinander abhängige Qualitätsmerkmale zu optimieren.
- „Sweetspot“ und „Design-Space“ Analysen, bei der die zu optimaler Qualität führenden Bereiche der Prozessparameter, das so-genannte Prozessfenster, genauer untersucht werden. Dies beinhaltet dann beispielsweise Prozessfähigkeits- und Risikoanalysen, um die Risiken nichtkonformer Qualität abzuschätzen und zu bewerten.
Zwischenfazit
In diesem Artikel haben wir die statistischen Methoden der Versuchsplanung (Design of Experiments – DOE) für Quality Engineering erläutert. Es wurden dabei die Vorzüge der statistischen Versuchsplanung im Gegensatz zu herkömmlichen Ansätzen zur Qualitätsoptimierung aufgezeigt.
Gerade im Bereich multivariater Qualitätsoptimierung oder bei starken Einschränkungen im zulässigen Versuchsbereich kommen oftmals komplexe Methoden der statistischen Versuchsplanung zum Einsatz. Auch in diesem Bereich helfen unsere Experten kompetent weiter, um Ihre Versuche effizient und effektiv zu planen!
Exkurs: Unvollständiger Versuchsplan
Wie kann ich einen balancierten unvollständigen Versuchsplan erstellen?
Angenommen, Hautkrebsforscher möchten drei verschiedene Sonnencremes testen. Dazu werden auf die Oberseiten der Hände eines Probanden zwei verschiedene Sonnencremes aufgetragen. Nach einer Bestrahlung durch UV-Licht werden anschließend die Hautschädigungen in Form von Sonnenbrand protokolliert.
Die linke und rechte Hand der Probanden bilden die Versuchsobjekte innerhalb eines Blocks (ein Block ist ein Proband in diesem Beispiel). Durch die Berücksichtigung des Blockeffekts ist es möglich davon auszugehen, dass beide Hände einer Person die identische Eigenschutzzeit aufweisen und eventuelle Unterschiede in der anschließenden Hautrötung tatsächlich auf die unterschiedliche Schutzwirkung der beiden Sonnencremes zurückzuführen sind und nicht auf unterschiedliche Hauttypen.
Ein balancierter unvollständiger Versuchsplan kann mit der Funktion design.bib aus dem R-Paket agricolae erzeugt werden. Dort anzugeben sind die Anzahl der Behandlungen (v = 3 Sonnencremes) und die Blockgröße (k = 2 Hände). Der genaue Befehl hierfür lautet design.bib ( trt = 1:3 , k = 2 , seed = 42 ). In der unten tabellierten Versuchsplanung wird in jedem Block oben die Behandlung der linken und unten die der rechten Hand aufgelistet. Beachten Sie hierbei, dass der Versuchsplan zufällig konstruiert wird und daher von der Saat Ihres Zufallszahlengenerators abhängt.
| Block | Behandlung |
| 1 | 2 |
| 1 | 3 |
| 2 | 1 |
| 2 | 2 |
| 3 | 3 |
| 3 | 1 |
Es werden b = 3 Blöcke und damit 3 Probanden benötigt, um einen balancierten unvollständigen Versuchsplan zu erhalten.
Die verwendeten Parameter der statistischen Versuchsplanung werden in der folgenden Tabelle festgehalten:
| v | Anzahl an Behandlungen |
| b | Anzahl an Blöcken |
| r | Anzahl an Blöcken, welche eine bestimmte Behandlung beinhalten |
| k | Anzahl an Behandlungen in einem Block |
| λ | Anzahl an Blöcken, welche zwei bestimmte Behandlungen beinhalten |
Die beiden Parameter v = 3 und k = 2 waren vom Versuchsleiter vorgegeben. Die restlichen drei Parameter werden von der Software dazu passend gewählt. 2 Blöcke (2 und 3) beinhalten die Behandlung 1 und entsprechendes gilt auch für die Behandlungen 2 und 3. Von daher ist r = 2 (r steht für repeat = Wiederholungen). Nur ein Block (3) enthält gleichzeitig die Behandlungen 1 und 2 und entsprechendes gilt für die Paare (1,3) und (2,3) von Behandlungen. Deshalb ist λ = 1.
Wann kann ich überhaupt einen balancierten unvollständigen Versuchsplan erstellen?
Ein Versuchsplan gilt als vollständig, falls in jedem Block jede Behandlung mindestens einmal vorkommt. Das ist aus verständlichen Gründen in diesem Beispiel nicht möglich, weil 3 Sonnencremes getestet werden, Menschen aber für gewöhnlich nur 2 Hände besitzen. Beispielsweise fehlt im ersten Block die erste Behandlung. Daher ist dieser Versuchsplan nicht vollständig. Man kann aber auch nicht immer auf einen balancierten unvollständigen Versuchsplan ausweichen. Für die Existenz eines BIBD sind die folgenden drei hinreichenden Bedingungen zu überprüfen:
- Die Anzahl an Behandlungen ist in jedem Block identisch. (k = 2)
- Jede Behandlung kommt in der gleichen Anzahl an Blöcken vor. (r = 2)
- Jedes Paar an Behandlungen kommt in der gleichen Anzahl an Blöcken vor. (λ = 1)
Wenn Sie diese drei hinreichenden Bedingungen und die genannten Parameterwerte (in Klammern) für dieses Beispiel mit der oben tabellierten Versuchsplanung vergleichen, werden Sie feststellen, dass es sich hier tatsächlich um einen balancierten unvollständigen Versuchsplan handelt.
Neben den hinreichenden Bedingungen gibt es auch notwendige Bedingungen für die Existenz eines BIBD:
- bk = vr
- λ(v-1) = r(k-1)
Diese notwendigen Bedingungen dienen dazu, geeignete Parameter für einen balancierten, unvollständigen Versuchsplan zu finden. Für die Existenz eines BIBD reicht es nicht aus, die fünf Parameter eines Versuchsplans auf die Einhaltung der notwendigen Bedingungen zu testen. Dafür sind in einem konkreten Versuchsplan die hinreichenden Bedingungen zu überprüfen. Allerdings kann man Parameterkombinationen ausschließen, wenn sie die notwendigen Bedingungen nicht einhalten. Dadurch lassen sich die für ein BIBD in Frage kommenden Parameterkombinationen deutlich beschränken, was bei der Auffindung eines solchen Versuchsplans hilfreich sein kann.
Wie Sie sehen, gibt es also Situationen, in denen kein balancierter unvollständiger Versuchsplan erstellt werden kann. Wenn Sie einen konkreten Versuch planen und einen Versuchsplan erstellen wollen, wählen Sie deshalb zunächst die Anzahl an Behandlungen insgesamt (v) und die Anzahl an Behandlungen in einem Block (k). Vielleicht haben Sie auch schon eine Vorstellung zur Anzahl der Wiederholungen r einer Behandlung oder der Anzahl an Blöcken b. Die verbliebenen beiden Parameter können Sie dann berechnen, indem Sie das obige Gleichungssystem (notwendige Bedingungen) lösen. Ist dieses nicht lösbar oder ergibt unsinnige Werte, existiert kein BIBD für diese Parameter. Dann sollten Sie die Parameter ändern. Ansonsten können Sie das BIBD gemäß der hinreichenden Bedingungen erstellen oder die Berechnung einfach Ihrer Statistik-Software überlassen.
So können Sie den Versuchsumfang erhöhen
Die obige statistische Versuchsplanung hat einen sehr kleinen Versuchsumfang mit gerade einmal 2 Wiederholungen einer Behandlung. Denn falls der Parameter r bei der R-Funktion nicht angegeben wird, erstellt die Funktion automatisch eine kleinstmögliche Versuchsplanung mit r = 2. Um die Anzahl jeder einzelnen Behandlung beispielsweise von 2 auf 4 zu verdoppeln, sollten Sie den Parameter r = 4 explizit angeben und mit dem Befehl design.bib ( trt = 1:3 , k = 2 , r = 4 , seed = 42 ) den Versuchsplan erstellen.
| Block | Behandlung |
| 1 | 1 |
| 1 | 2 |
| 2 | 3 |
| 2 | 1 |
| 3 | 3 |
| 3 | 2 |
| 4 | 3 |
| 4 | 1 |
| 5 | 2 |
| 5 | 1 |
| 6 | 3 |
| 6 | 2 |
mit Inzidenzmatrix:
| Behandlung | Block 1 | Block 2 | Block 3 | Block 4 | Block 5 | Block 6 |
| 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 2 | 1 | 0 | 1 | 0 | 1 | 1 |
| 3 | 0 | 1 | 1 | 1 | 0 | 1 |
Und so sieht das ganze in R aus:
Statistische Versuchsplanung mit Novustat
Zu Anfang dieses Artikel haben wir für Sie die Motivation begründet, einen statistischen Versuchsplan zu erstellen. Wir hoffen, dass wir Ihnen mit unserer Expertise in diesem Artikel eine Entscheidungshilfe für die Wahl zwischen einem vollständigen und einem unvollständigen Versuchsplan bieten konnten und Sie unsere Schilderung des Vorgehens zur Erstellung eines balancierten unvollständigen Versuchsplans in R für Ihr eigenes Projekt nutzen können. Wichtig ist jedoch zu beachten, dass dies nur ein Schritt auf dem Weg zu einem professionellen Forschungsplan ist. Wenn Sie einen Unterstützungsbedarf bei Ihrer Forschungskonzeption haben, kontaktieren Sie uns gern. Novustat unterstützt Sie individuell und kurzfristig in Ihrer statistischen Versuchsplanung bzw. wenn Sie einen Versuchsplan erstellen wollen!
Wir unterstützen Sie gerne individuell und bedarfsgerecht bei Ihrer statistischen Versuchsplanung. Unser Expertenteam von über 80 Statistikern ist versiert im Umgang mit der Planung von statistischen Versuchen aller Art.
Ihr Plus bei NOVUSTAT für die statistische Versuchsplanung
Als Statistik-Service-Dienstleister unterstützen wir Sie bedarfsgerecht:
- Jahrelange Erfahrung: Bereits über 1000 Kunden durften wir bei ihrem Statistik-Projekt betreuen
- Expertise in allen gängigen Statistik-Programmen (R, SPSS, Stata, Rapidminer usw.)
- vollständige Unterstützung in allen Belangen der statistischen Versuchsplanung (Bestimmung minimaler Versuchsumfang, Konstruktion des Versuchs, Störgrössen eliminieren usw.)
- auch im weiteren Verlauf unterstützen wir Sie mit Fragebogenerstellung, Hypothesenbildung usw. sowie
- Interpretations-Unterstützung der Ergebnisse
- Darstellung der Ergebnisse (Erstellung von Grafiken)
Welche Aspekte sind für die DoE Design of Experiments relevant?
Natürlich lässt sich nicht alles vorausplanen. Sie wissen nicht vorab, welche Messwerte Sie erhalten oder ob Ihre Hypothesen sich bestätigen. Sie können aber sehr wohl die Stichprobengröße so planen, dass statistisch signifikante Ergebnisse überhaupt möglich werden oder mögliche „Threats to validity“ (Gültigkeitsgrenzen) vorhergesehen und vermieden werden. Wenn erst bei der Diskussion Ihrer Ergebnisse die Frage aufkommt, ob unterschiedliche Vorerfahrung von Experimentteilnehmern die beobachteten Unterschiede verursacht haben könnten, Sie aber im Fragebogen nicht nach diesen Erfahrungen gefragt haben, dann verliert ihre Studie an Aussagekraft. Darum sollten Sie alle Hindernisse für statistisch signifikante Ergebnisse oder für die Gültigkeit der Ergebnisse während der Planungsphase schon diskutieren.
Wo sich während der Versuchsplanung noch offene Fragen auftun, kann man Experten befragen, nach Erfahrungen anderer recherchieren oder eine kleine Vorstudie durchführen, z.B. Probeinterviews oder Probemessungen und dann schon vorab diese kleine Statistik auswerten. In der industriellen Fertigung müssen aufwändige Pilotversuche durchgeführt werden, bevor ein Produkt oder ein Prozess serienmäßig eingesetzt wird. Zu den Vorversuchen zählen beispielsweise Prototypenversuche, Zuverlässigkeitstests, oder Vorserien. Dabei wird unter anderem die Lebensdauer eines Produktes ermittelt, der Einfluss von unterschiedlichen Bedingungen getestet, oder eine Optimierung des Prozesses durchgeführt.
Versuche kosten einem Unternehmen Geld, benötigen Zeit und Ressourcen. Statistische Methoden zur Versuchsplanung helfen, den notwendigen Aufwand hierfür so gering wie möglich zu halten um einen möglichst großen Erkenntnisfortschritt zu erlangen.
Typische statistische Versuchsplanung und deren Bestandteile
Folgende Aktivitäten und Ergebnisse gehören zur statistischen Versuchsplanung (englisch: DoE Design of Experiments):
Planung/Vorbereitung
- Auswahl der Variablen und Messmethoden: Welche Variablen eignen sich am besten dazu, die Forschungsfrage zu beantworten? Innerhalb welches Versuchsraums sollen diese Variablen liegen? Mit welchen Messmethoden erhebt man diese Variablen am verlässlichsten?
- Berechnen der minimalen Stichprobenzahl: Wie viele Personen muss man befragen, wie viele Projekte auswerten, wie viele Datenpunkte messen oder wie viele Datensätze sammeln, um statistisch signifikante Antworten auf die Forschungsfrage zu erhalten?
- Stichprobenerhebung und Gruppenzuordnung: Mit welchem Verfahren werden am besten Stichproben erhoben, so dass sie repräsentativ sind? Wie werden die Teilnehmer Gruppen zugeordnet, so dass diese möglichst ähnlich sind?
Durchführung
- Diskussion der verschiedenen Aspekte der Gültigkeit / Validität der Ergebnisse, insbesondere Inhaltsvalidität, Kriteriumsvalidität, Konstruktvalidität und Verallgemeinerbarkeit. Wie können diese vorab durch das Versuchsdesign vermieden oder möglicherweise kritische Faktoren geprüft werden?
- Umgang mit Störeffekten: Kann ein störender Effekt vorab eliminiert werden? Muss er stattdessen konstant gehalten werden oder durch Blockbildung oder Randomisierung neutralisiert?
- Planung der Durchführung: Das Ergebnis der Versuchsplanung ist ein genauer Projektplan, der genau beschreibt, welche Aktivitäten mit welchen Methoden und durch welche Person durchgeführt werden, welches Ergebnis erzeugt, wie viel Aufwand dafür veranschlagt wird und zu welchem Termin fertiggestellt werden soll. Auch Störeffekte, die durch eine suboptimale Versuchsdurchführung entstehen können, lassen sich vorab durch eine gute Planung vermeiden und sind daher für die statistische Versuchsplanung hochrelevant. Dazu gehört beispielsweise, dass eine Codierung unabhängig durch zwei Forscher durchgeführt wird. Manchmal ist das Ergebnis der sorgfältigen Versuchsplanung, dass mehr Personen, Durchläufe oder Messgeräte nötig werden als gedacht. Wir unterstützen Sie, diese rechtzeitig zu beantragen und beschaffen.
Datenauswertung
- Planung der Datenauswertung: Noch bevor die ersten Daten erhoben werden, muss festgelegt sein, mit welchem Werkzeug die Auswertungen durchgeführt werden. Eventuell kann ein Probelauf frühzeitig Planungsfehler offenbaren.
Statistische Versuchsplanung und Novustats Leistungen
Wir von Novustat erstellen gerne eine komplette Versuchsplanung für Ihr Vorhaben, prüfen Ihren bereits vorliegenden Versuchsplan oder diskutieren mit Ihnen gemeinsam die passende Planung für Ihr Projekt. Vier Augen sehen mehr als zwei!
Beauftragen Sie also Novustat möglichst frühzeitig in Ihrem Projekt, noch bevor Sie die ersten Daten erheben. Wir begleiten gerne den gesamten Arbeitsprozess mit, aber es kann auch Sinn machen, sich nur für die Versuchsplanung den Rat von Experten einzuholen und dann weiterzusehen, bei welchen Schritten eine weitere Unterstützung nützlich wäre.
Wir unterstützen Sie gerne bei Ihrer statistischen Versuchsplanung oder DoE Design of Experiments, unsere Statistiker helfen Ihnen gerne weiter. Unser Team von über 80 professionellen Statistikern unterstützt Sie gerne individuell und qualitätsgeprüft bei Ihrer statistischen Versuchsplanun
Weitere Quellen:
ICH (International Conference on Harmonization) Q10 (2008), “Pharmaceutical quality system”
FDA (Food and Drug Administration) (2011), “Guidance for Industry: PAT – A Framework for Innovative Pharmaceutical Development, Manufacturing and Quality Assurance”
Juran, J.M. (1992), „Juran on Quality by Design: The New Steps for Planning Quality into Goods and Services“
Montgomery, D. C. (1997), “Design and Analysis of Experiments”
Kleppmann, W. (2013), „Versuchsplanung. Produkte und Prozesse optimieren“
Weiterführende Links
[1] https://qe-informatik.uibk.ac.at/
[2] https://de.wikipedia.org/wiki/Statistische_Versuchsplanung