Gute statistische Modelle sind stabile, einfache, funktionale Zusammenhänge zwischen Einflussfaktoren und einer oder mehreren Zielvariablen. Stabilität bedeutet, dass das Modell nicht nur die erhobenen Daten optimal beschreibt, sondern auch für zukünftige Messungen (Prognose) anwendbar und allgemein gültig ist. Der Zusammenhang soll dabei so einfach wie möglich und so komplex wie nötig sein. Statistische Modelle sind Hilfsmittel, um die reale Welt etwas besser zu verstehen. Hat man nun endlich ein Modell gebildet, bleibt am Ende oft die Frage: Wie gut ist das Modell eigentlich? Zur Beurteilung der Modellgüte haben sich im linearen Modell das Bestimmtheitsmass R2 etabliert sowie der mittlere quadratische Fehler (engl. Mean Square Error oder kurz MSE), bzw. dessen Wurzel RMSE. Für das logistische Modell zeigen wir Ihnen, wie sie anhand einer Receiver Operating Characteristic die Fläche unter der ROC Kurve (engl. ROC Curve) als Masszahl für die Modellgüteheranziehen können. Ausserdem besprechen wir das sogenannte Pseudo-R2.
Bei Fragen zur Modellbildung oder allen anderen Fragen rund um das Thema Modellierung stehen Ihnen unsere Experten zur Verfügung. Wir bieten Ihnen ein breites Angebot von der Statistik-Beratung bis hin zur Statistik Auswertungen. Nehmen Sie Kontakt mit uns auf!
Folgende Fragen beantwortet dieser Artikel
- Wie beurteilt man die Güte (Fit) eines statistischen Modells?
- Welche Masszahlen gibt es hierfür?
- Wie berechnet man die Modellgüte in linearen Modell: Mean Square Error (MSE), RMSE und Bestimmtheitsmass R2 bzw. R2adj
- Welche Masszahlen gibt es im logistischen Modell? (z.B. ROC Kurve (ROC Curve), Area under the Curve (ROC AUC))
Die Güte (engl. Fit) eines Modells: Wie gut ist das Modell?
Wie gut ist das Modell?
Um es gleich vorab zu sagen: Darauf gibt es keine pauschale Antwort!
Philosophisch gesehen sollte ein gutes Modell aber mindestens stabil, einfach und universal gültig sein. Dies alles in einer mathematischen Kennzahl zusammenzufassen ist nicht möglich, zumal Begriffe wie „einfach“ auch unterschiedlich ausgelegt werden.
Die gebräuchlichen Masszahlen für die Modellgüte betrachten den Unterschied zwischen beobachteten Werten und den vom Modell vorhergesagten Werten. Bei einem sogenannten Informationskriterium wird ausserdem die Komplexität eines Modells strafend berücksichtigt.
MSE, RMSE, R2, ROC Curve, ROC AUC etc. – Welche Masszahl ist geeignet?
Die Masszahl für den Fit eines Modells ist im Wesentlichen vom Modell selbst abhängig. Für lineare Modelle mit stetiger Zielvariable und normalverteilten Fehlerterm wird das Bestimmtheitsmass R2, das adjustierte Bestimmtheitsmass R2adj oder der mittlere quadratische Fehler (Mean Square Error – MSE) oder dessen Wurzel (RMSE) verwendet.
Ist die Zielvariable dichotom (2 Ausprägungen, z.B. ja/nein) erfolgt die Modellierung oftmals über ein logistisches Modell. In diesem Modell werden sogenannte Pseudo- R2 (Nagelkerke, Cox-Snell, McFadden) berechnet. Alternativ kann die Modellgüte aber auch über die ROC Curve (Receiver-Operating-Characteristic) und der Fläche unter der Kurve (ROC AUC) angegeben werden.
Für die Auswahl der Masszahl ist es wichtig, ob die Masszahl nur dafür verwendet werden soll, um die Güte eines Modells zu beschreiben- in diesem Fall ist die Wahl der Kennzahl für den Modelfit prinzipiell dem Anwender überlassen. Im Sinne einer guten wissenschaftlichen Praxis muss diese Kennzahl aber im Vorfeld festgelegt und in der Arbeit beschrieben werden.
Wesentlich schwieriger wird es allerdings, wenn verschiedene Modelle miteinander verglichen werden sollen. Anhand der Modellgüte soll dabei letztendlich das „beste“ Modell gekürt werden. Dabei ist zu beachten, dass es keine allgemeingültigen Kriterien gibt.
Häufig werden verschiedene Modelle dann mit allgemeinen Masszahlen wie beispielsweise Residuen (relativ zum beobachteten Wert) untereinander verglichen.
Bestimmte Kennzahlen wie z. B. das Bestimmtheitsmass sind von der Anzahl der Einfussvariablen abhängig: Je mehr Variablen im Modell sind, desto höher fällt R2 aus, unabhängig davon, welchen Informationsgehalt die Variable tatsächlich hat.
Einen Überblick über die wichtigsten Kennzahlen der Modellgüte ist in folgender Abbildung dargestellt.
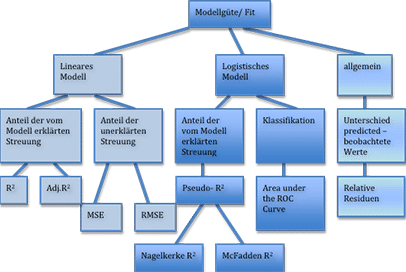
Die Berechnung und die Interpretation der einzelnen Kennzahlen für die Modellgüte betrachten wir in den folgenden Abschnitten anhand von Beispielen.
Beispiel Modellgüte: Arbeitsmotivation
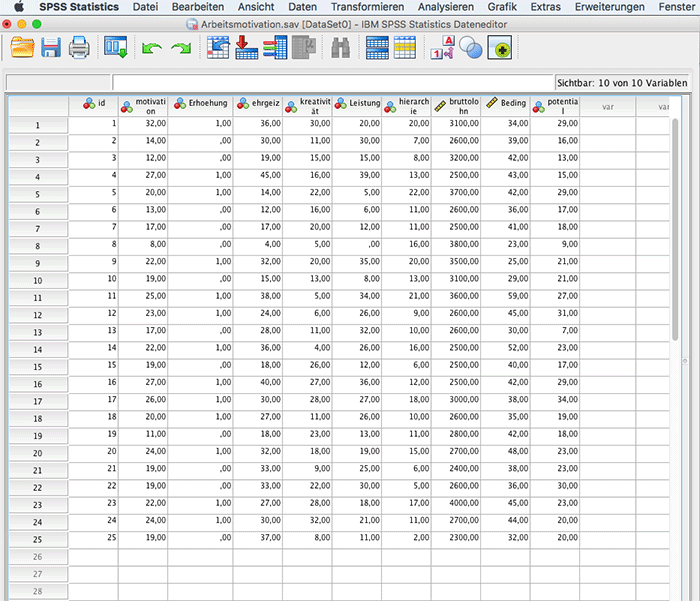
Für die folgenden Berechnungen verwenden wir einen Datensatz mit n=25 Beobachtungen. Ein Arbeitgeber hat von 25 Mitarbeitern Daten zur Motivation am Arbeitsplatz (Zielvariable Y). Die Motivation soll in Abhängigkeit von verschiedenen Prädiktoren beschrieben werden. Mögliche Prädiktoren sind Kreativität, Leistungsstreben, Position in der Hierarchie des Unternehmens, Bruttolohn pro Monat, und Lernpotential der Tätigkeit.
Zuerst soll in einer linearen Regression die stetige Variable Motivation durch die Prädiktoren modelliert werden. Anschliessend wird ein logistisches Modell verwendet, um die dichotome Variable Lohnerhöhung in Abhängigkeit dieser Faktoren zu modellieren.
Die Auswertungen hierzu werden mit SPSS durchgeführt. Eine kurze Programmeinführung zu SPSS finden Sie in unseren Serviceseiten.
R2 und mean square Error (MSE) – Modellgüte im linearen Modell
Für dieses Beispiel soll die Motivation in Abhängigkeit von dem Leistungsstreben des Mitarbeiters modelliert werden. Hierz wird ein einfaches lineares Modell verwendet. Dazu wählt man in der Menüleiste von SPSS Analysieren – Regression – Linear... . Als abhängige Variable wird die Zielvariable Motivation eingegeben, als Einflussvariable wird Leistungsstreben eingesetzt. Für die Berechnung der Modelgüte muss im Untermenü Statistiken der Punkt Anpassungsgüte des Modells aktiviert sein. Mean Square Error wird nicht automatisch berechnet. Um diesen im Anschluss manuell zu berechnen ist es hilfreich, sich die vom Modell vorhergesagten Werte ausgeben zu lassen. Dafür muss im Menü Speichern Vorhergesagte Werte – nicht standardisiert angekreuzt werden.
Abbildung 3 Lineare Regression in SPSS
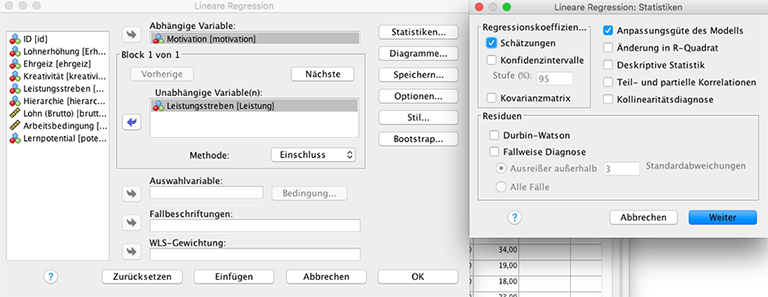
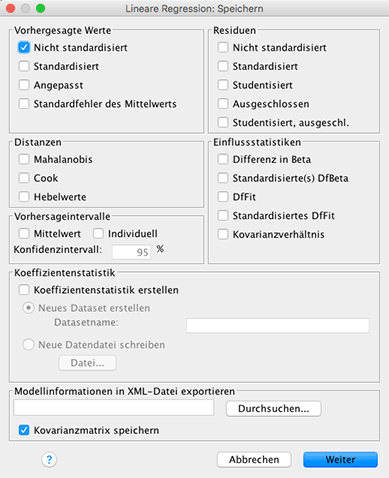
Bestätigt man mit Weiter, so erhält man folgende Ausgabe
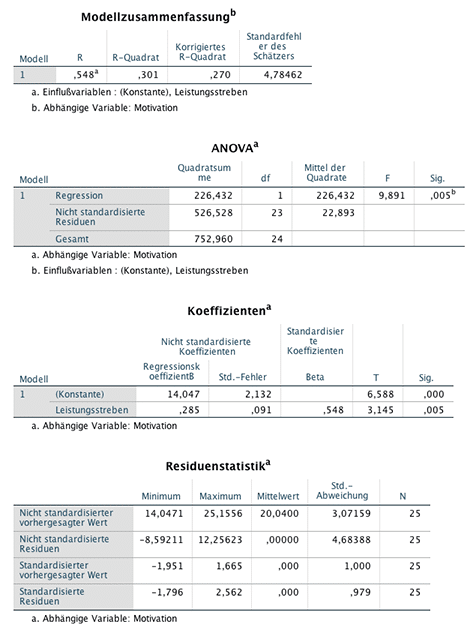
Bestimmtheitsmass R²: Wieviel Streuung kann das Modell erklären?
In der Tabelle Modellzusammenfassung wird das Bestimmtheitsmass R2=0,301 sowie das adjustierte R2 =0,270 (Korrigiertes R-Quadrat) angegeben. Die ANOVA Tabelle testet, ob das Modell insgesamt einen Erklärungsbeitrag für die Zielvariable liefert. In der Tabelle Koeffizienten kann man den Intercept und den Regressionskoeffizienten entnehmen sowie die zugehörigen Kenngrössen. Aus der Tabelle Residuenstatistik kann man Informationen bezüglich der Residuen, d.h. der Differenz zwischen beobachtetem und vorhergesagtem Wert entnehmen.
Anhand der Zahlen können wir folgendes interpretieren:
Leistungsstreben und Motivation besitzt einen positiven Zusammenhang der Art, dass mit einem erhöhtem Leistungsstreben auch eine hohe Motivation verbunden ist (R=0,548). Ändert sich das Leistungsstreben um eine Einheit, so ist damit eine Erhöhung der Motivation um den Faktor 0,285 verbunden (Regressionskoeffizient = 0,285; p=0,005). Mit diesem Modell kann 30,1% der in den Daten vorkommenden Streuung erklärt werden (R2=0,301). Die höchste Abweichung zwischen vorhergesagtem und beobachtetem Wert (Motivation) liegt bei 12,26 (s. Tabelle Residuenstatistik).
Mean square Error (MSE) und RMSE: Wie weit weichen die Daten von der Vorhersage ab?
Um den Mean Square Error (MSE) zu berechnen muss man zunächst die quadrierten Residuen berechnen. Dazu wählt man im Datenfenster Transformieren – Variable berechnen... und gibt die Berechnungsformel wie in folgender Abbildung gezeigt ist ein. Daraufhin wird eine neue Variable res_sq an den Datensatz angefügt.
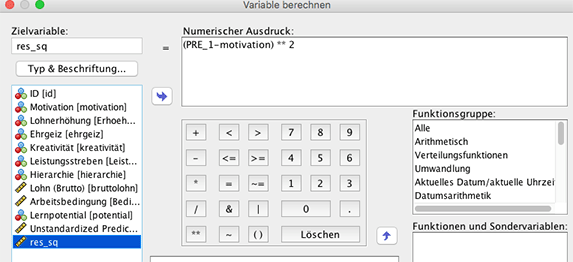
Das arithmetische Mittel der quadrierten Residuen wird als Mean Square Error (MSE) bezeichnet. Die Wurzel aus Mean Square Error heisst RMSE.
Um diese Berechnung von RMSE durchzuführen muss man in SPSS bei Analysieren – Deskriptive Statistik den Mittelwert von res_sq berechnen lassen. Dies führt zu folgender Ausgabe:

Der mittlere quadratische Fehler liegt bei 21,0611 (MSE), der RMSE bei 4,589 (\(\sqrt{21,0611}\)).
R², MSE und RMSE interpretieren: Ist mein Modell wirklich gut?
Ob das Modell nun gut oder schlecht ist, lässt sich nicht generell sagen, auch nicht mithilfe der berechneten Gütemasse. 30% der Streuung können durch das Modell erklärt werden, da ist noch Platz nach oben. Allerdings ist die Erklärung mit dem Modell besser als gar keine (ANOVA: p=0,005)!
Die RMSE = 4,589 gibt an, dass die durchschnittliche Distanz der beobachteten Datenpunkte von der Regressionsgerade 4,589 Einheiten (vertikal) beträgt.
Vielleicht lässt sich das Modell durch Hinzunahme weiterer Variablen verbessern?
Modellgüte mit vielen Einflussfaktoren: R2 und MSE im multiplen linearen Modell
Wie ändert sich die Modellgüte, wenn zusätzliche Prädiktoren aufgenommen werden? Führen wir nochmals eine lineare Regression durch, allerdings nehmen wir noch 3 zusätzliche Prädiktoren in das Modell auf: Kreativität, Position in der Hierarchie des Unternehmens und Bruttolohn pro Monat. Damit ergibt sich folgende Ausgabe:
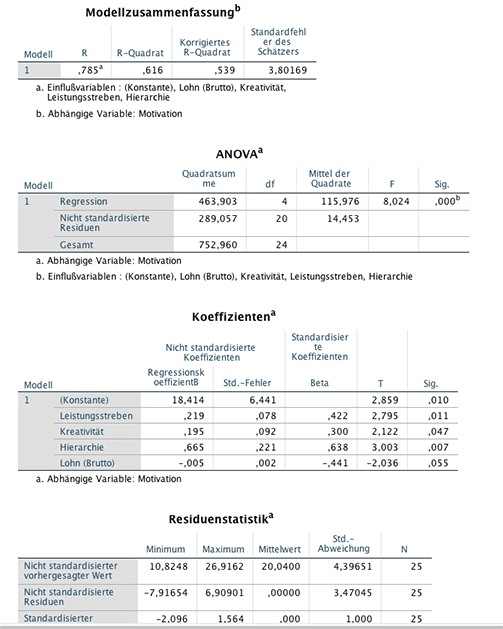
Interpretation – Was sagen die Zahlen aus?
Das Bestimmtheitsmass hat sich auf R2=0,616 erhöht durch die Hinzunahme weiterer Prädiktoren. Durch die 4 Einflussvariablen kann das Modell 60 % der in den Daten vorhandenen Streuung erklären. Das adjustierte R2 liegt mit einem Wert von R2 adj=0,539 unter dem Bestimmtheitsmass. Das liegt daran, dass R2 adjustiert einen Strafterm enthält, der die Anzahl der Einflussvariablen sowie die Fallzahl berücksichtigt. Das Modell soll ja so einfach wie möglich bleiben. Modelle mit unterschiedlicher Anzahl von Parametern können sinnvoll nur mit Gütekriterien verglichen werden, die die Anzahl der Parameter berücksichtigen.
Die ANOVA Tabelle zeigt, dass das Modell insgesamt eine Erklärung für die Zielvariable liefert (F=8,0254, p<0,001). In der Tabelle Koeffizienten werden die Regressionskoeffizienten angegeben und in der Tabelle Residuenstatistik sieht man, dass sich die extremen Residuen auf -7,9 bzw. 6,9 reduziert haben. Berechnet man Mean Square Error und RMSE analog zu der einfachen linearen Regression, so ergeben sich folgende Werte:
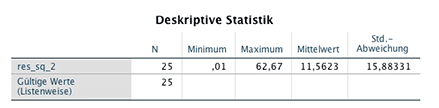
Mean Square Error (MSE)=11,5623, RMSE=3,40. Die Kennzahlen Mean Square Error und RMSE haben sich auch gegenüber dem linearen Modell reduziert.
Pseudo-R2 und ROC AUC der ROC Curve – Modellgüte im logistischen Modell
Liegt eine dichotome Zielvariable (2 Ausprägungen, z. B. ja/nein) vor, so ist eine logistische Regression meist ein geeignetes Modell. Als Ergebnis einer logistischen Regression erhält man in Abhängigkeit von den Prädiktoren geschätzte Wahrscheinlichkeiten für das Eintreffen eines Ereignisses.
Pseudo-R2 – gibt es tatsächlich!
Einige Statistiker und Mathematiker haben versucht, die Berechnung des Bestimmtheitsmasses an diese Situation anzupassen: Die beobachteten Werte haben die Ausprägung 0 und 1 (oder können dahin transformiert werden), die vorhergesagten Werte liegen im Bereich von 0 bis 1. Die Interpretation dabei ist gleich: Pseudo R2 gibt die vom Modell erklärte Streuung an, liegt zwischen 0 und 1 und hohe Werte sprechen für eine gute Anpassung des Modells an die Daten. Eine Auflistung verschiedenster Ansätze ist in Wikipedia zu finden. SPSS verwendet den Ansatz von Nagelkerke bzw. Cox Snell.
Wie bei allen Kennzahlen gilt auch hier: Man kann nur gleiches mit Gleichem sinnvoll vergleichen. Da es viele Pseudo-Masse gibt, ist es wichtig genau auf die Bezeichnung zu achten.
Receiver Operating Characteristic (ROC Curve) und Area under the curve (ROC AUC)
Gerade im logistischen Modell bietet sich noch eine weitere Möglichkeit an, die Modellgüte zu beurteilen. Die Vorhersagewerte im logistischen Modell sind stetig und liegen im Bereich von 0 bis 1. Sie werden als Auftretenswahrscheinlichkeiten gedeutet. Was heisst jetzt aber: Patient A hat eine geschätzte Auftretenswahrscheinlichkeit für eine Krankheit? Ist er nun krank oder nicht? Um aus den vorhergesagten Wahrscheinlichkeiten eine ja/nein Aussage zu gewinnen, muss ein Schwellenwert (Trennwert, Grenzwert, threshold value) festgesetzt werden: Wahrscheinlichkeiten unter diesem Wert werden der einen Kategorie zugeordnet, predicted values, die darüber liegen, der anderen Kategorie. Die Wahl des Grenzwertes ist dem Anwender überlassen. Die Festsetzung des Grenzwertes führt dazu, dass die predicted values in eine dichotome Variable überführt werden.
Nun ist es möglich, die beobachteten Werte konkret mit den dichotomisierten predicted values des Modells zu vergleichen. Für jeden Grenzwert kann eine Vierfeldertafel angegeben werden, in dem korrekt zugeordnete, falsch positive und falsch negative Zuordnungen dargestellt sind.
| beobachtet | predicted | |
| 0 | 1 | |
| 0 | 🙂 | 🙁falsch positiv |
| 1 | 🙁falsch negativ | 🙂 |
Abbildung 9 Klassifikationstabelle
ROC Curve
In einer Receiver Operating Characteristic (kurz ROC Kurve oder engl. ROC curve) werden für alle möglichen Grenzwerte die relativen Häufigkeiten der richtig positiv klassifizierten Fälle (y-Achse) gegen die relativen Häufigkeiten der falsch positiv klassifizierten (x-Achse) abgetragen. Somit erhält man Kurven, die durch den Wert (0/0) und (1/1) gehen.
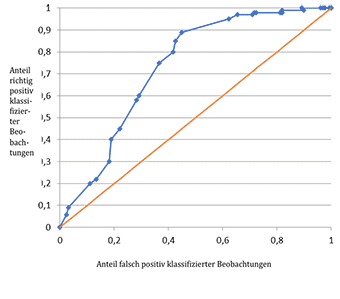
Die denkbar schlechteste Möglichkeit eines statistischen Modells zur Vorhersage einer dichotomen Zielvariable ist der pure Zufall, z. B. ausgedrückt in Form eines Münzwurfes. Wirft man eine Münze, um daraus die Zielvariable vorherzusagen, so hat man für jeden möglichen Grenzwert gleich viele richtig positive und falsch positive Fälle. Die ROC curve ist in diesem Fall die Winkelhalbierende. Je mehr sich die ROC curve des statistischen Modells von der Winkelhalbierenden unterscheidet, um so zuverlässiger und besser sagt das Modell die beobachteten Werte vorher. In obiger Graphik ist die Zufälligkeit mit der roten Winkelhalbierenden gekennzeichnet.
Area under the curve (ROC AUC)
Als Masszahl zur Beschreibung einer Kurve hat sich die Fläche unter der Kurve (engl. Area under the curve ROC AUC) durchgesetzt. Aufgrund des Wertebereichs der x-und y- Werte hat die Winkelhalbierende eine Fläche von 0,5 Einheiten. Der beste Test, der in jeder Situation die dichotome Zielvariable richtig vorhersagt, hat eine ROC AUC von 1. Logistische Regressionsmodelle sind also umso besser, je näher ihre ROC AUC bei 1 liegt. Umgekehrt zeigen schlechte logistische Regressionsmodelle in der ROC curve eine ROC AUC bei 0,5.
Logistische Regression am Beispiel Arbeitsmotivation
Betrachten wir das Vorgehen anhand obigen Beispiels: Der Personalchef bietet einigen seiner Mitarbeitern eine Lohnerhöhung an. Die Information Lohnerhöhung (ja/nein) ist im Datensatz in der Variable Erhöhung abzulesen. Im Folgenden wollen wir die Zielvariable Erhöhung in Abhängigkeit von dem Prädiktoren Leistungsstreben modellieren. Dazu berechnen wir ein logistisches Modell in SPSS.
Hierzu wird die logistische Regression über Analysieren – Regression – binär logistisch... aufgerufen.
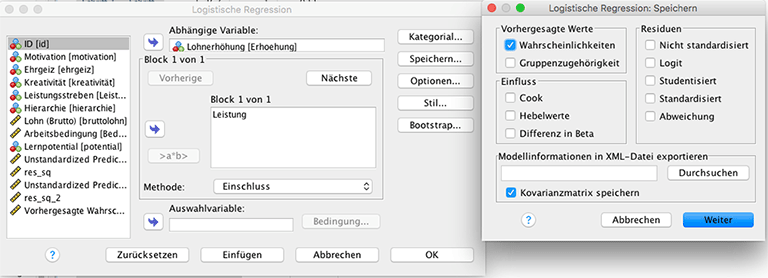
Im Untermenü Speichern wählen wir dann bei Vorhergesagte Werte – Wahrscheinlichkeiten aus. Die Gruppenzugehörigkeit macht zunächst noch keinen Sinn, da wir ja den optimalen Grenzwert noch nicht kennen. Die Standardeinstellung bei SPSS liegt bei 0,5.
Bestätigung mit Weiter erzeugt folgende Ausgabe:
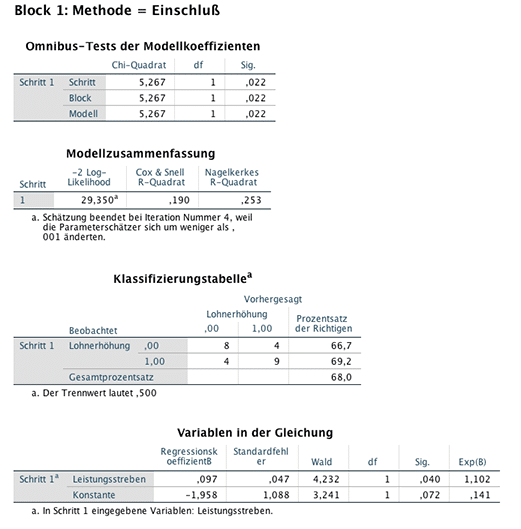
Die Modellzusammenfassung zeigt ein Pseudo R2 nach Cox und Snell von 0,190 und Nagelkerkes R2 von 0,253. Die Werte sind im unteren Bereich. Einen grossen Teil der Variabilität der Daten kann das Modell demzufolge nicht erklären. Dennoch zeigt der Omnibus Test, dass das Modell eine Erklärung liefert, die besser ist als eine Münze zu werfen (Chi-Quadrat=5,267, p=0,022). Die Tabelle Variablen in der Gleichung gibt die Regressionskoeffizienten an. In der Klassifizierungstabelle sind die Anzahlen der richtig und falsch klassifizierten Beobachtungen abzulesen. Allerdings ist diese Tabelle für einen Trennwert von 0,5 erstellt. Um zu sehen, welcher Trennwert für das Modell optimal ist, muss eine Receiver Operating Characteristic (ROC Kurve bzw. ROC curve) berechnet werden.
ROC Curve berechnen
Dazu wählt man Analysieren – ROC-Curve. Die Variablen werden dann wie in der folgenden Abbildung eingegeben.
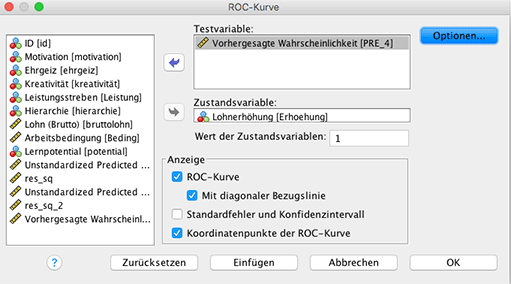
Dies führt zu folgender Ausgabe:
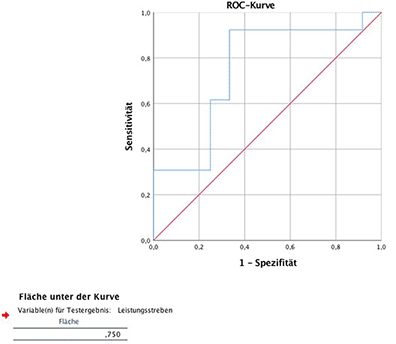
In der Abbildung der ROC Kurve (ROC curve) erkennt man, dass die blaue Linie, die aus dem Modell stammt, sich von der roten Linie der Zufälligkeit unterscheidet und absetzt. Eine genaue Auflistung aller möglichen Trennwerte mit zugehörigen x-und x-Werten der ROC curve ist in folgender Abbildung zu sehen.
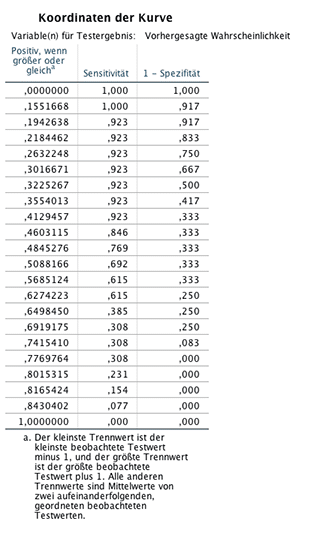
Dadurch, dass nur 25 Beobachtungen vorliegen, zeigt die ROC curve Sprünge. Die von der blauen Kurve und der x-Achse eingeschlossene Fläche beträgt ROC AUC=0,750, liegt also genau zwischen 1 (Maximum) und 0,5 (Minimum). Eine Verbesserung des Fits könnte durch Hinzunahme weiterer Prädiktoren erfolgen.
Zusammenfassung
Die Beurteilung der Modellgüte ist ein zentrales Thema in der statistischen Modellierung. Auch im Kontext von Data Mining werden oft zahlreiche Modelle gebildet, um anschliessend das Beste zu selektieren. In diesem Zusammenhang ist die Festlegung sinnvoller und vergleichbarer Kriterien für die Modellgüte wichtig. Dabei sollte man nicht nur die Anpassung der vorhergesagten Werte an die Daten beachten. Denn auch die Komplexität der Modelle spielt eine wichtige Rolle. Universelle Gütekriterien existieren nicht. Jedes Modell hat eigene Kennzahlen, z.B. ROC curve und ROC AUC im logistischen Modell und mean square Error (MSE), RMSE oder Bestimmtheitsmass im linearen Modell. Auch die Interpretation ist nicht immer einfach. Modelle mit kleinen Gütezahlen können oftmals in der Praxis wichtiger sein als Modelle mit einem hohen Bestimmtheitsmass. Feste Regeln dafür gibt es nicht.
Gute Modelle können immer nur in enger Zusammenarbeit mit Statistikern und Anwendern gebildet werden. Unsere Experten unterstützen sie bei ihren Projekten. Nehmen Sie Kontakt mit uns auf!