Mathematische Definitionen wirken mitunter kompliziert und wenig einleuchtend. Die Bayessche Regel macht da keinen Unterschied. Dabei ist sie grundlegend wichtig, nicht nur für die Bayessche Statistik. Die meisten empirischen Studien basieren auf Schllussfolgerungen eben durch diese Regel. In diesem Artikel wollen wir sie daher im Detail erläutern und anhand eines einfachen Satz von Bayes-Beispiel untersuchen.
Sie möchten wissen wie Sie den Satz von Bayes wann anwenden und was genau hinter der Bayessche Regel steckt und wie diese einzusetzen ist? – Dann wenden sie sich dafür an uns für eine professionelle Beratung.
In diesem Artikel erklären und zeigen wir Ihnen:
- Grundlegende Definitionen und Erkläuterungen zu: Bayessche Regel und bedingte Wahrscheinlichkeit
- Wie man den Satz von Bayes wann anwenden kann sowie
- Ein hilfreiches und unterstützendes Beispiel, das den Satz von Bayes verständlich erklärt.
Die bedingte Wahrscheinlichkeit einfach erklärt
Die Grundlage, um den Satz von Bayes zu verstehen, ist die sogenannte bedingte Wahrscheinlichkeit. Ihr Formelzeichen wird wie folgt geschrieben:
P(A/B)
Gelesen wird dies: P ist die Wahrscheinlichkeit, dass ein gewisses Ereignis A eintritt, wenn vorher ein gewisses Ereignis B eingetreten ist. Also beispielsweise könnte A ein Lottogewinn sein und B ein gezogener bzw. erworbener Lottoschein. Dann würde man also wie folgt lesen: P ist die Wahrscheinlichkeit, im Lotto zu gewinnen, vorausgesetzt man hat vorher einen Lottoschein gezogen. Das klingt auf den ersten Blick etwas unschlüssig, aber man muss sich vorstellen, dass P(A) die allgemeine Wahrscheinlichkeit ist, im Lotto zu gewinnen. Auch ohne Spielschein.
Die bedingte Wahrscheinlichkeit wird definiert über die Formel:
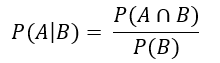
Hier beschreibt P(A ∩ B) die Wahrscheinlichkeit, dass A und B gemeinsam auftreten. P(B) dagegen bezeichnet allein die Wahrscheinlichkeit des Eintretens von B. Folglich errechnet sich in unserem Beispiel die bedingte Wahrscheinlichkeit für den Lottogewinn mit vorherigem Kauf eines Lottoscheins aus der gemeinsamen Wahrscheinlichkeit eines Lottogewinns unter der Bedingung, einen Schein gezogen zu haben, geteilt durch die Wahrscheinlichkeit, dass man sich auch tatsächlich (zuvor) einen Schein gekauft hat.
Sollten Sie konkrete Fragen zu diesem Thema haben, zögern Sie bitte nicht uns anzusprechen. Wir freuen uns auf Ihre Anfrage über das Kontaktformular!
Was muss ich wissen, um den Satz von Bayes wann anwenden zu können?
Die Bayessche Regel lautet bekanntlich:
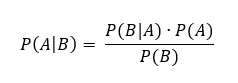
Der Trick ist also das Umdrehen der bedingten Wahrscheinlichkeit von P(B/A) zu P(A/B). Um vereinfacht zu erklären, was damit konkret gemeint ist, nachfolgend ein Satz von Bayes-Beispiel:
Aktuell und in aller Munde ist das Beispiel eines medizinischen Schnelltests. P(B) ist hier die Wahrscheinlichkeit, dass eine bestimmte Krankheit vorliegt. P(A) dagegen die Wahrscheinlichkeit, dass ein Test positiv anschlägt. Eine wichtige Überlegung dazu lautet: Warum gilt nicht P(A/B) = P (B/A)? Die bedingte Wahrscheinlichkeit behandelt demnach zwei unterschiedliche Fragestellungen:
„Wie lautet die Wahrscheinlichkeit, dass ein Test positiv ist, wenn die Patientin die Krankheit hat?“ = P(A/B)
„Wie lautet die Wahrscheinlichkeit, dass eine Patientin die Krankheit hat, wenn der Test positiv ist? = P(B/A)
Das sind zwei sehr unterschiedliche Aussagen und genau aus diesem Grund ist die Bayessche Regel so wichtig! Ein einfaches Gleichsetzen der Wahrscheinlichkeiten würde falsche Aussagen treffen.
Brauche ich einen Satz von Bayes Rechner?
In der nachfolgenden Visualisiereung ist das eben genannte Satz von Bayes-Beispiel grafisch dargestellt. Die Zahlen wurden vereinfacht, um den Sachverhalt klar erkennbar zu machen. Hier lässt sich sehr schnell erkennen, dass ein Umdrehen der bedingten Wahrscheinlichkeit nicht einfach dechungsgleich möglich ist. Konkret: Wenn eine Patientin erkrankt ist, dann zeigt der Test mit 90 % Wahrscheinlichkeit ein positives Ergebnis. Aber wenn der Test positiv ist, dann ist die Patientin nur mit 8,3 % Wahrscheinlichkeit auch tatsächlich krank.
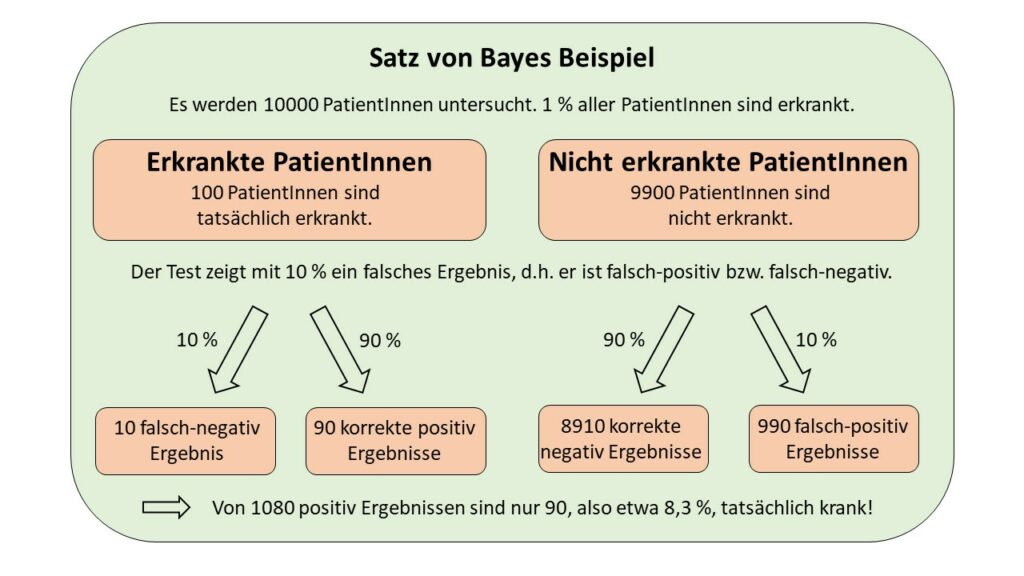
Man muss nur die Bayessche Regel anwenden, um diesen Zahlen zu erklären, ein spezieller Satz von Bayes Rechner ist dafür nicht nötig:
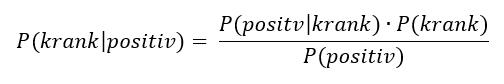
Setzen wir nun die Werte ein, die wir oben in der Grafik festgelegt haben, so ergibt sich folgendes Ergebnis:
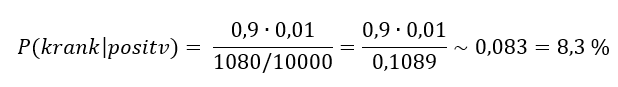
Die Zahlen decken sich eindeutig und plausibel mit den Überlegungen aus dem Schaubild. Dies ist nur eine von vielen Anwednungsmöglichkeiten, um den Satz von Bayes beispielhaft darzustellen. Jede Art von medizinischen Tests zeigt eine Möglichkeit, wie wir den Satz von Bayes wann anwenden können.
Jetzt ganz konkret: Den Satz von Bayes wann anwenden?
Wie eingangs erwähnt gibt es eine Menge an Anwendungsgebieten für die Bayessche Statistik, die immer auf der hier vorgestellten Regel basiert. Im Bereich von Big Data werden sogenannte Bayes-Klassifikatoren angewendet. In der Bioinformatik, den Neurowissenschaften und vielen weiteren Wissenschaften gibt es Verfahren, die den Satz von Bayes dann anwenden, wenn eine Schlussfolgerung umgedreht werden muss. Die bedingte Wahrscheinlichkeit umzudrehen ermöglicht also die verschiedenen statistischen Tests.
Wenn Sie einen konkreten Anwendungsfall odr eine Problemstellung haben und einen Satz von Bayes Rechner benötigen, dann nehmen Sie gerne Kontakt mit uns auf. Wir bieten professionelle Statistik-Beratung zu diesem und vielen anderen statistischen Themen!
Weiterführende Links
- https://www.mun.ca/biology/scarr/4250_Bayes_Theorem.html
- https://probabilityandstats.wordpress.com/2017/09/04/bayes-formula-gives-better-perspective-on-medical-testing/
- https://corporatefinanceinstitute.com/resources/data-science/bayes-theorem/
- https://medium.com/m/global-identity?redirectUrl=https%3A%2F%2Ftowardsdatascience.com%2Fwhat-is-bayes-rule-bb6598d8a2fd