Wenn wir uns im Internet über statistische Verfahren oder auch Machine Learning Algorithmen informieren, stossen wir früher oder später auf die Diskussion zwischen der sogenannten Bayes Statistik und der klassischen Statistik mit Hypothesentest und p Wert. Was man aber nur selten dazu findet, sind verständliche Erklärungen, wo die Unterschiede zwischen den beiden Ansätzen liegen und was das für die Anwender bedeutet. Mit diesem Artikel wollen wir das ändern: Wie erklären Ihnen einfach und verständlich wesentliche Grundlagen der Bayes Statistik und zeigen mögliche Stärken und Schwächen auf.
Wenn Sie dazu Fragen haben, zögern Sie nicht sich bei uns zu melden! Wir bieten professionelle Coachings zu diesen und vielen weiteren Themen rund um Statistik an. Wenden sie sich hierzu an uns für eine professionelle Beratung!
Die Definition der Wahrscheinlichkeit
Wo liegen nun die Unterschiede zwischen klassischer Statistik, auch frequentistische Statistik genannt, und der Bayes Statistik? Dazu muss man wissen, dass Statistik immer auf einer bestimmten Definition von Wahrscheinlichkeit basiert. In der untenstehenden Abbildung haben wir die Definitionsunterschiede einmal gegenübergestellt. Einige Begriffe, die man im Zusammenhang mit Statistik häufig hört, haben wir der jeweiligen Methode zugeordnet.

Auf den ersten Blick mag es so wirken, als wäre Wahrscheinlichkeit in der Bayes Statistik stärker wie ein Gefühl definiert. Doch das täuscht: Beiden Ansätze liegen eindeutig definierte mathematische Regeln zugrunde. Vorweg gilt es zu betonen, dass in den meisten alltäglichen Anwendungsfällen beide Methoden die gleichen identen Ergebnisse liefern. Das ist gut und wichtig, denn sonst gäbe es ja eine klare Entscheidung vorab, welche Methode richtig und damit besser wäre.
Bayes Statistik in der Praxis: a priori und a posteriori
In der Bayes Statistik geht man vorab mit einer bestimmten Erwartung an statistische Auswertungen heran. Diese Erwartung nennt man a priori Wahrscheinlichkeit. Sie besteht also bereits, bevor wir uns die Ergebnisse eines bestimmten Experiments anschauen.
Stellen wir uns folgendes Szenario vor: Es soll untersucht werden, mit welcher Wahrscheinlichkeit beim Münzwurf Kopf fällt (also ob die Münze manipuliert ist). Aus seiner Erfahrung im Glücksspiel geht der Bayessche Statistiker davon aus, dass die Wahrscheinlich in etwa bei 50 % liegen wird (der Statistik Experte würde hier fomulieren: die a priori Wahrscheinlichkeit sei eine eng gestreute Normalverteilung um den Mittelwert p = 0.5 mit einer Standardabweichung SD = 0.1).
Im nächsten Schritt geht es nun an das Daten sammeln: Die Münze wird viermal geworfen. Dabei – so nehmen wir mal an – fällt viermal Zahl. Ist zwar ungewöhnlich, aber nicht völlig unwahrscheinlich. Die Wahrscheinlichkeit dafür beträgt p = 0.5*0.5*0.5*0.5 = 0.0625 = 6,25 %. Der Bayes Statistiker schreitet nun zur Tat und aktualisiert entsprechend seine Vorstellung. Dies funktioniert nach bestimmten Algorithmen, die alle auf dem Satz von Bayes basieren. Er kommt zu dem Schluss, dass die Erwartung nach unten zu korrigieren ist.
Die sogenannte a posteriori Wahrscheinlichkeit beträgt nunmehr 43 % für Kopf (und demzufolge 57 % für Zahl). Die Schlussfolgerung aus dem Experiment für den Bayes Statistiker: Die Münze scheint manipuliert.
Für konkrete Fragen zur Bayes Statistik und zu klassischer Wahrscheinlichkeit zögern Sie nicht, sich bei uns zu melden! Unser erfahrenes Team bietet professionelle Hilfe und individuell zugeschnittene Coachings!
Was sagt die klassische Statistik: p Wert
In der klassischen Statistik untersucht man mittels Hypothesentest, ob Kopf bzw. Zahl mit einer Wahrscheinlichkeit von 50 % fallen. Diese Annahme formulieren wir in der soganannten Nullhypothese. Auf Basis eines Signifikanzniveaus von 95 % ist der entsprechende p Wert des Chi-Quadrat Tests kritisch (hier: für viermal Zahl bei vier Würfen).
Eine Signifikanz von 95 % bedeutet: die Wahrscheinlichkeit, dass wir uns irren, wenn wir die Nullhypothese verwerfen, liegt bei maximal 5 %. In unserem konkreten Fall liegt diese – als p Wert bezeichnete – Wahrscheinlichkeit nun unter 5 %. Folglich verwirft der Statistiker die Nullhypothese und nimmt an, dass die Münze nicht mit 50 % Wahrscheinlichkeit Kopf zeigt, also nicht fair ist.
Wo liegt der Unterschied in den Interpretationen? Die Schlussfolgerung ist in beiden Fällen ähnlich: Beide Ansätze gehen nicht länger davon aus, dass die Münze mit jeweils 50 % Kopf bzw. Zahl zeigt. Was sich aber grundlegend unterscheidet, ist der Informationsgehalt: Die Bayes Statistik hat zusätzlich noch die a posteriori Wahrscheinlichkeit berechnet. Damit lässt sich die wohl begründete Vermutung äussern, wie hoch die tatsächliche Wahrscheinlichkeit für Kopf (und damit auch für Zahl) mit dieser Münze ist. Dies können klassische Statistik und p Wert nicht.
Und jetzt nochmal: Was genau besagt der Satz von Bayes?
Der Satz von Bayes, oder auch Bayes Theorem genannt, wurde 1763 vom Mathematiker Thomas Bayes entwickelt. Entgegen der landläufigen Meinung bildet dieses Theorem auch die Grundlage für die klassische frequentistische Statistik. Es handelt sich um eine logische und recht einfache Folgerung aus der Definition der bedingten Wahrscheinlichkeit.
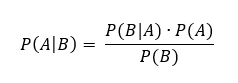
Diese Formel lässt sich wie folgt interpretieren: Die Wahrscheinlichkeit, dass A eintritt, unter der Bedingung, dass B bereits eingetreten ist, entspricht dem Quotient aus der Wahrscheinlichkeit das B eintritt, wenn A eingetreten ist, multipliziert mit der Wahrscheinlichkeit für A und der Wahrscheinlichkeit für B.
Klingt auf den ersten Blick kompliziert, aber wir machen es gleich verständlicher. Um zu verstehen, wie die Bayes Statistik diese Formel nutzt, um Schlussfolgerungen über die a posteriori Wahrscheinlichkeit zu ziehen, werfen wir einen Blick auf die folgende Umformulierung des Satz von Bayes (Ws = Wahrscheinlichkeit):

Die Plausibilitätsfunktion ist hier als das Ergebnis des statistischen Experiments zu verstehen. Die Multiplikation der a priori Wahrscheinlichkeit mit der Plausibilitätsfunktion führt also zu a posteriori Wahrscheinlichkeit. (Im Englischen bezeichnet man diese Anpassung auch als ‘Bayesian Updating’). Die marginale Wahrscheinlichkeit ist schwierig zu verstehen und sollte hier einfach als eine Art Skalierungsfaktor verstanden werden.
Wo liegen nun Stärken und Schwächen der Bayes Statistik?
Einerseits wird in der Bayes Statistik die bisherige Erfahrung der Wissenschaft in Form der a priori Wahrscheinlichkeit berücksichtigt. Dies ist eine wichtige Besonderheit, denn sie erlaubt es bereits mit sehr geringen Fallzahlen, wohl fundierte Schlüsse zu ziehen. Wenn man es nämlich ganz genau nimmt, dann sind vier Münzwürfe mathematisch gar nicht dazu geeignet, einen Hypothesentest mit p Wert durchzuführen. Klarer Pluspunkt für die Bayes Statistik!
Weiters ist die Interpretation der a posteriori Wahrscheinlichkeit gemeinhin sehr intuitiv und gut verständlich. Das Ergebnis der Berechnungen nach dem Satz von Bayes liefert eine mathematisch saubere Schätzung für die Wahrscheinlichkeit, mit der bestimmte Ereignisse eintreten. Es lassen sich auch Regressionsanalysen und verschiedene Methoden des Machine Learnings mit Bayes Statistik-Methoden realisieren.
Zusammenfassend mag es nun so scheinen, als wäre die Bayes Statistik besser geeignet als die klassische frequentistische Statistik. Aber so pauschal lässt sich das nicht behaupten: Die Bayessche Statistik hat auch Schwächen: Sie benötigt wesentlich mehr Rechenkraft und dauert dementsprechend oftmals deutlich länger. Ausserdem ist die Wahl der a priori Wahrscheinlichkeit eine Herausforderung und nicht immer eindeutig und klar bestimmbar.
Warum Sie zur Bayes Statistik wechseln sollten
Gerade im Bereich der Sozialwissenschaften und der Medizin (Biostatistik), wenn nur eine begrenzte Anzahl an Testobjekten zur Verfügung steht, liefert die Bayes Statistik zuverlässige Ergebnisse und eine höhere Aussagekraft als der p Wert der klassischen Statistik. Auch in der Marktforschung wird mehr und mehr auf die neu-entdeckte Bayessche Statistik zurückgegriffen. In einem folgenden Artikel werden wir daher weitere konkrete Anwendungen der Bayes Statistik im Detail erläutern. Gerne unterstützen wir auch Sie in Form einer Statistik-Beratung, ob und wie Bayes Statistik zu Ihrem Forschungsfeld passt!