Viele der geläufigen parametrischen statistischen Methoden gehen von normal verteilten Daten aus. Dazu gehören der t-Test, ANOVA, Regression und zahlreiche andere statistische Tests. Auch wenn Sie Ihre Daten standarisieren indem Sie für z Transformation SPSS nutzen, unterstellen Sie eine Normalverteilung der Daten.
Was aber tun, wenn der SPSS Test auf Normalverteilung negativ ausfällt? Nicht normal verteilte Daten können gerade bei kleineren Stichproben parametrische Tests ungültig werden lassen. Um für eine z-Transformation SPSS zu nutzen sollten in jedem Fall normal verteilte Daten vorliegen. In allen Fällen kann eine Transformation oft schnell Abhilfe schaffen.
In diesem Artikel wollen wir Ihnen daher eine schnelle und einfache Anleitung zum transformieren Ihrer Daten geben.
Ausreisser entfernen
Wenn beim Test auf Normalverteilung SPSS eine nicht normale Verteilung anzeigt, kann dies durch Ausreisser bedingt sein. Bevor Sie die Normalverteilung testen, sollten Sie in jedem Fall Ausreisser ausschliessen. Wir empfehlen Ihnen Ausreisser mit Hilfe von Boxplots zu identifizieren und auszuschliessen.
Verteilung bestimmen
Der nächste Schritt sollte dann eine visuelle Inspektion der Daten sein. Dies kann durch Q-Q Plot und Histogramm geschehen. Notieren Sie sich dabei folgende Punkte:
- Liegt eine rechts- oder linksschiefe Verteilung vor?
- Wie stark weicht die Verteilung von einer Normalverteilung ab?
- Welchen Wert haben der Minimalwert und der Maximalwert der Verteilung?
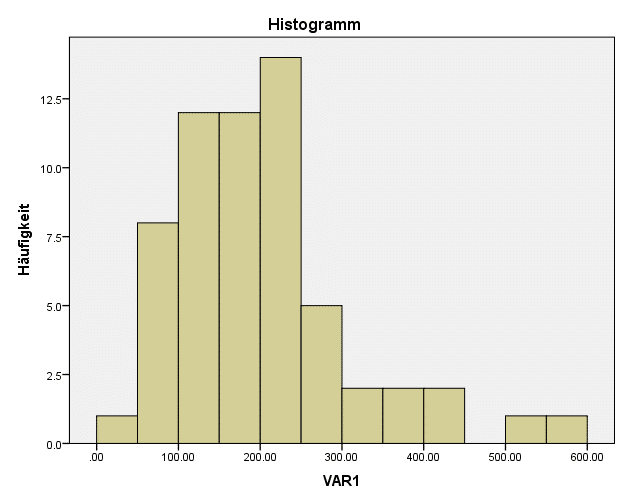
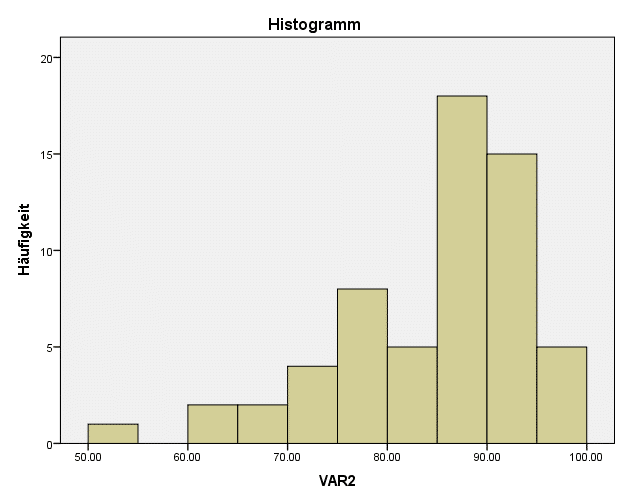
Das weitere Vorgehen hängt davon ab, ob es sich um eine rechts- oder linksschiefe Verteilung handelt. Dabei gestaltet sich das Transformieren einer rechtsschiefen Verteilung ein klein wenig leichter. Wir zeigen Ihnen daher zuerst wie Sie mit rechtsschiefen Verteilungen umgehen.
Rechtsschiefe Verteilung transformieren
In diesem Artikel werden wir auf die drei häufigsten Transformationen eingehen. Diese sind in der folgenden Tabelle dargestellt. X gibt dabei immer den zu transformierenden Wert und Min den Minimalwert der Verteilung an.
| Transformation | Geeignet für | Formel | Erläuterung |
| Wurzeltransformation | Schwache Abweichung von Normalität | \({ \sqrt[]{x+a} }\) | Wenn \(Min < 1:\) a = (\(Min\) * -1) + 1 Wenn \(Min < 1:\) a = 0b: Basis des Logarithmus ( empfohlen: \(\textit{e }oder\textit{ }10\ \) ) |
| Logtransformation | Mittlere bis starke Abweichung von Normalität (je nach Basis) | \( log_{b} \left( x+a \right) \) | |
| Inverse Transformation | Starke Abweichung von Normalität | \(\frac{1}{x+a}\ast-1 \) |
Wie Sie sehen wird bei jeder Transformation zuerst eine Konstante a zum Wert addiert. Dies dient dazu, den Wert vor der Transformation mindestens auf 1,0 zu setzen.
Am einfachsten erledigen sie die Transformation Ihrer Daten in SPSS mit der Syntax. Erstellen Sie dazu zuerst eine neue Syntax in SPSS.
Im Syntax Fenster können Sie dann mit Hilfe des COMPUTE Befehls transformierte Variablen erstellen. Im folgenden Beispiel wird eine rechtsschiefe Variable mit einem Minimum von 0 transformiert.:
*** Transformation für rechtsschiefe Daten ***.
COMPUTE VAR1_SQR =SQRT(VAR1+1). /* Wurzeltransformation.
COMPUTE VAR1_Lgn=LN(VAR1+1). /* Logtransformation mit Basis e.
COMPUTE VAR1_Lg10= LG10(VAR1+1). /*.Logtransformation mit Basis 10.
COMPUTE VAR1_INV =(1/(VAR1+1))*-1. /* Inverse Transformation.
EXECUTE.
Anschliessend können die transformierten Variablen auf Normalverteilung geprüft werden. Dies geschieht wieder durch Histogramme und Q-Q Plots.
In unserem Beispiel weicht die Verteilung nur leicht von einer Normalverteilung ab. Der SPSS Test auf Normalverteilung zeigt bereits, dass eine Wurzeltransformation ausreicht, um eine annähernd normale Verteilung zu erhalten.

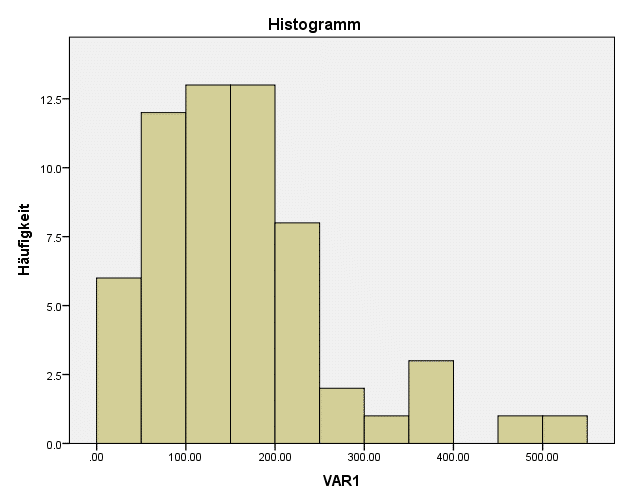
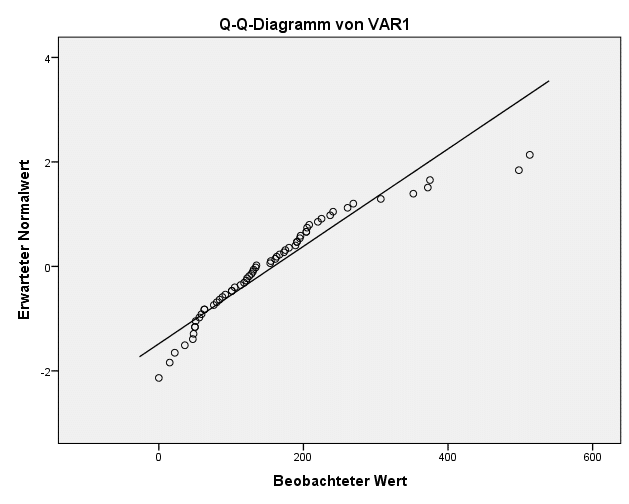
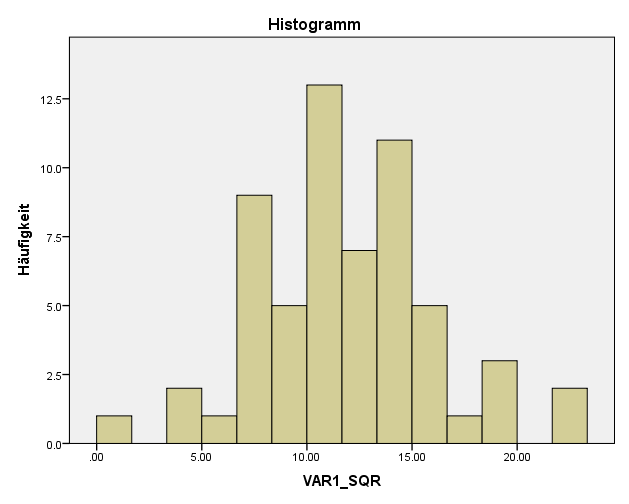
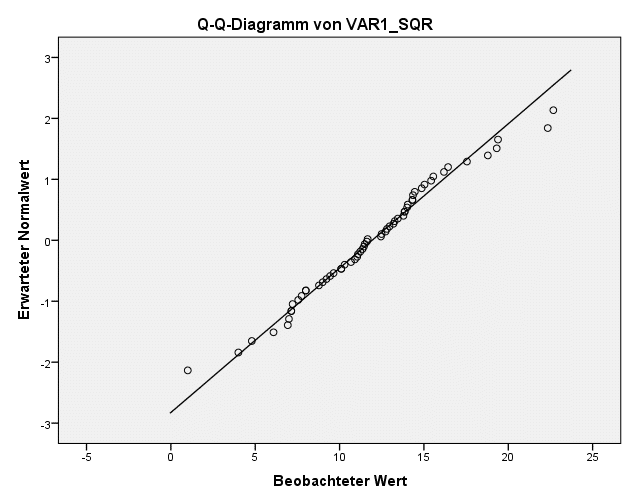
Die Daten aus der Wurzeltransformation könnten also für Verfahren, die eine Normalverteilung annehmen (wie parametrische Tests oder z-Transformation SPSS) verwendet werden.
Gleichzeitig ist auch zu erkennen, dass eine starke Transformationen wie die inverse Transformationen die Verteilung noch verschlechtert.
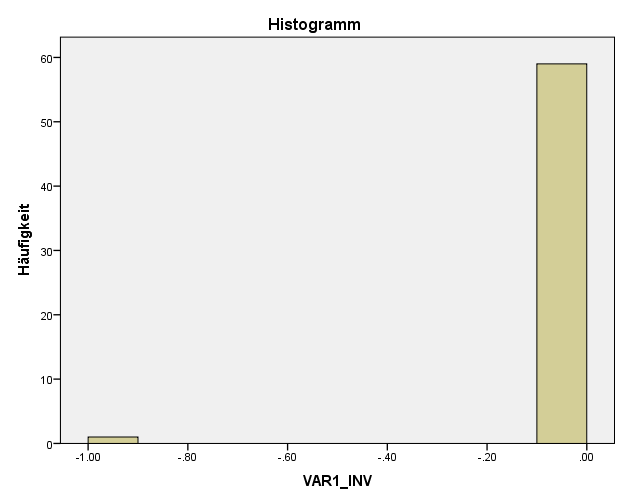
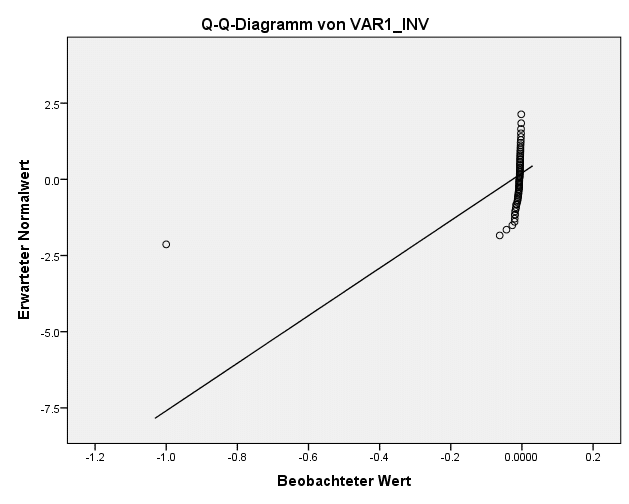
Die schwach rechtsschiefe Verteilung wurde in eine starke linksschiefe Verteilung umgewandelt. Diese Transformation ist also nur bei sehr starken Abweichungen von der Normalverteilung sinnvoll.
Linksschiefe Verteilung transformieren
Bei einer linksschiefen Verteilung verfahren Sie ähnlich wie bei einer rechtsschiefen Verteilung. Sie müssen lediglich noch einen zusätzlichen Schritt ausführen: Da die gängigen Transformationen für rechtsschiefe Verteilungen geeignet sind, reflektieren Sie vor der Transformation Ihre linksschiefe Variable einfach. So erhalten Sie eine rechtsschiefe Verteilung.
Dazu multiplizieren Sie alle Werte mit -1. Zusätzlich addieren Sie noch eine Konstante zur Variable um alle Werte mindestens auf 1,0 zu setzen:
\( x_{ref}= \left( x\ast-1 \right) +a\)
Mit dem reflektierten Wert führen Sie dann die Transformation durch. Nach der Transformation multiplizieren Sie den Wert wieder mit -1 um die Reihenfolge der Werte wiederherzustellen. Dieses Verfahren wird noch einmal in der folgenden Tabelle zusammengefasst:
| Transformation | Geeignet für | Formel | Erläuterung |
| Wurzeltransformation | Schwache Abweichung von Normalität | \({ \sqrt[]{x_{ref}}\ast-1 }\) | \(x_{ref}= \left( x\ast-1 \right) +a \)
wenn \(Max>- 1:\) Wenn \(Max \leq – 1:\) b: Basis des Logarithmus (empfohlen: \(\textit{e }oder\textit{ }10\ \)) |
| Logtransformation | Mittlere bis starke Abweichung von Normalität (je nach Basis) | \(log_{b} \left( x_{ref} \right) \ast-1\) | |
| Inverse Transformation | Starke Abweichung von Normalität | \(\frac{1}{x_{ref}}\) |
Auch für linksschiefe Verteilungen führen Sie eine Transformation am Besten in der SPSS Syntax durch. Im folgenden Beispiel wurde eine Variable mit einem Maximalwert von 100 transformiert:
*** Transformation für linksschiefe Daten ***
* Werte reflektieren und auf Minimum von 1,0 setzen*.
COMPUTE VAR2_REF = (VAR2*-1)+101.
* Werte transformieren und dann erneut reflektieren.
COMPUTE VAR2_SQR =(SQRT(VAR2_REF))*-1. /* Wurzeltransformation.
COMPUTE VAR2_Lgn=(LN(VAR2_REF))*-1. /* Logtransformation mit Basis e.
COMPUTE VAR2_Lg10=(LG10(VAR2_REF))*-1. /*.Logtransformation mit Basis 10.
COMPUTE VAR2_INV =(1/VAR2_REF). /* Inverse Transformation.
EXECUTE.
In unserem Beispiel hat die Variable eine mittelstarke Abweichung von der Normalverteilung. Deshalb zeigt sich eine mittelstarke Transformation wie die Logtransformation als die effektivste.
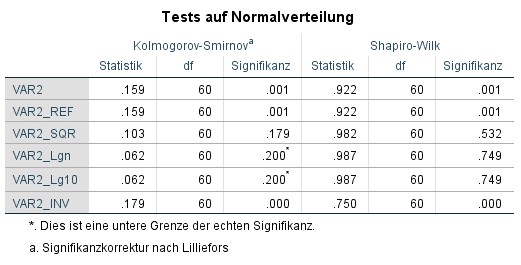
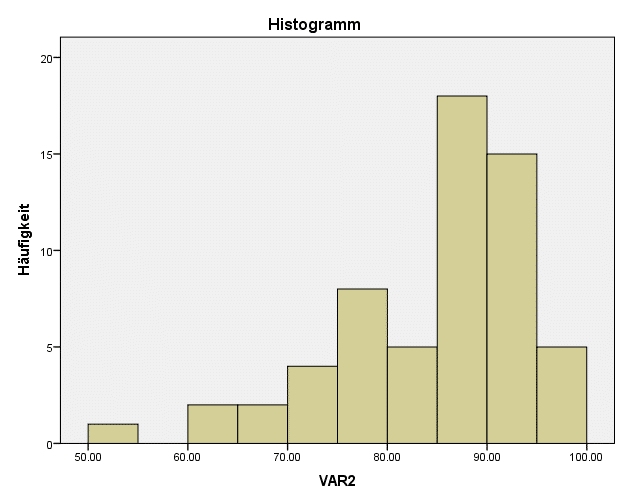
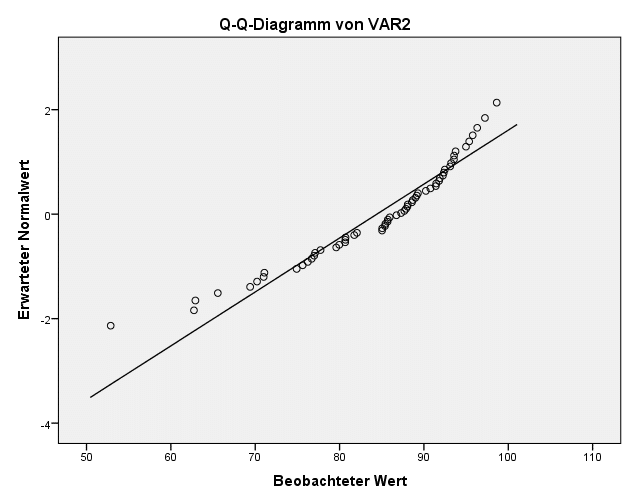
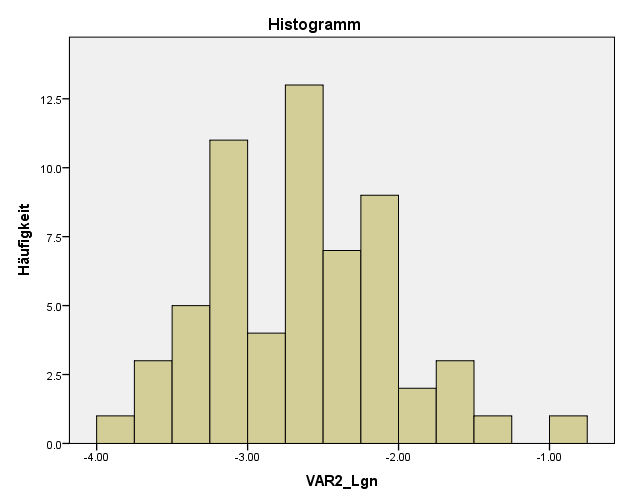
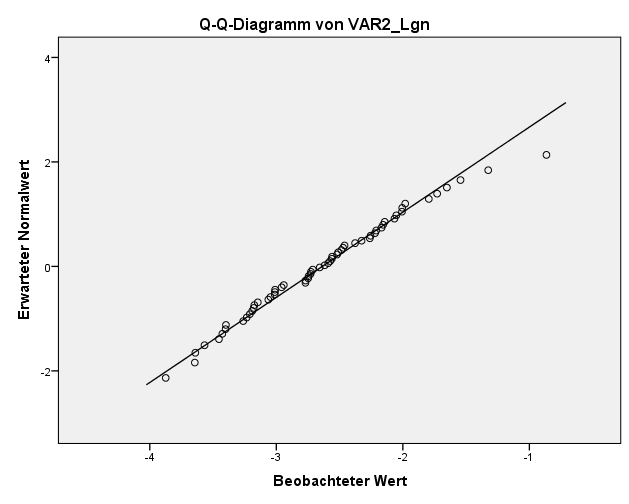
In diesem Fall könnte also die Logtransformation durchgeführt werden. Damit könnten auch für diese Variable parametrische Tests durchgeführt werden oder für ein z-Transformation SPSS verwendet werden.
Zusammenfassung: Bei fehlender Normalverteilung SPSS Transformationen verwenden
Wenn beim SPSS Test auf Normalverteilung eine nicht normale Verteilung anzeigt, heisst dies nicht zwingend, dass Sie auf parametrische Tests oder das Durchführen einer z Transformation in SPSS verzichten müssen. In diesem Artikel haben Sie gelernt wie Sie in wenigen Schritten durch eine Transformation eine normale Verteilung erhalten können.
Bei Verwendung von transformierten Werten sollten Sie aber stets beachten, dass unstandarisierte Kennzahlen wie Regressionskoeffizienten sich auf die transformierten Werten beziehen.
Gelegentlich kann es passieren, dass die gängigen Transformationen nicht weiterhelfen. In solch einem Fall muss bewertet werden ob die geplanten statistischen Verfahren robust gegenüber nicht normalen Daten sind oder ob Sie lieber auf nicht parametrische Verfahren zurückgreifen sollten. Unsere Experten können Ihnen bei Fragen zu dieser Thematik selbstverständlich kompetent weitergehend beraten!
Weiterführende Quellen
[1] https://scholarworks.umass.edu/items/e412a2c0-09f4-40d2-b971-d8f475fef67d
[2] http://www.biostathandbook.com/transformation.html
[3] https://www.ucl.ac.uk/child-health/user/login?destination=node/7147