Die Analyse von Daten zur Prozessdauer bzw. Überlebensdauer kann mit herkömmlichen statistischen Methoden zu schwerwiegenden Fehlinterpretationen der Daten führen. Wir haben bereits Techniken zur Überlebensanalyse (eng. survival analysis) präsentiert, die gruppenspezifische Risiken hinsichtlich einer Prozessdauer berechnet und vergleicht. In diesem Beitrag wollen wir die Cox Regression präsentieren, die eine multivariate Analyse von Daten zur Überlebensdauer ermöglicht.
Gerne unterstützen Sie unsere Expertinnen und Experten bei ihrer eigenen Studie im Rahmen einer Überlebensanalyse: von einer professionellen Statistik Beratung bis hin Datenauswertung und Hilfe bei der Berichterstellung. Wenden Sie sich dazu unverbindlich an uns!
In diesem Beitrag wollen wir folgende Punkte näher beleuchten:
- Was ist die Grundidee der Überlebensanalyse?
- Wir funktioniert die Coх Regression in der Theorie?
- Wie sieht ein Anwendungsbeispiel in SPSS inklusive der Anforderungen an die Datenstruktur aus?
Grundidee der Überlebenszeitanalyse
Die Überlebenszeitanalyse ist eine statistische Methode zur Untersuchung einer zeitlichen Dauer. Der Name deutet bereits darauf hin, dass die Methode ihre Ursprünge in der Biologie und der Medizin hat, als man – im wahrsten Sinne des Wortes – die Dauer bis zum Tod eines Organismus untersuchte.
Diese Methode ist allerdings nicht darauf begrenzt, denn es lassen sich grundsätzlich alle Zeiträume und jede zeitliche Fortdauer untersuchen, die durch ein benennbares Startereignis und ein benennbares Endereignis definiert sind. Aus diesem Grund ist die Methode auch unter dem Namen Ereignisanalyse (engl. event history analysis) bekannt.
Wozu benötigt man nun eine gesonderte Anwendung für die Analyse einer zeitlichen Dauer anstatt diese als schlichte metrische Grösse zu behandeln? – Eben genau das sollte man auf keinen Fall tun, besonders wenn Rechtszensierungen in den Daten vorliegen. Das bedeutet, dass der Zeitpunkt des Startereignisses bekannt ist, das Endereignis aber noch nicht eingetreten ist.
Ein Beispiel: Paar A war 10 Jahre verheiratet und ist nun geschieden, Paar B ist seit 5 Jahren verheiratet. Die Frage: Wessen Ehe dauert länger? lässt sich so natürlich nicht beantworten, da wir nicht wissen, ob und wie lange Paar B in Zukunft noch verheiratet sein wird.
Beide Zeiträume (bzw. zeitliche Dauern) bis zum Ereignis und bis zur Zensierung (also dem Ende der Beobachtungszeit) können jedoch bei einer Überlebenszeitanalyse genutzt werden, um die sogenannte bedingte Übergangsrate (engl. hazard rate) zu berechnen, also das aggregierte Risiko, dass ein Endereignis zu, jetzigen Zeitpunkt eintritt, wenn das bis dahin noch nicht geschehen ist. Daraus wiederum lässt sich die mittlere Prozessdauer, genannt Verweildauer, prognostizieren.
Cox Regression: Idee und Modell
Bei deskriptiven Methoden wie der Kaplan-Mayer-Schätzung wird die Übergangsrate für mehrere Zeitpunkte nach dem Startereignis auf Basis der bis dahin stattgefundenen individuellen Endereignisse bestimmt und damit wird das ‘Ableben’ der Stichprobe (ggf. aufgeteilt nach Gruppen) beschrieben.
Das Ziel einer multivariaten Modellierung ist eine explizitere und passgenauere Beschreibung der Wirkung der Kofaktoren. Cox Regression nimmt dafür die Existenz einer über die Zeit konstanten Basisrate an. Je nach der Zusammensetzung der Kovariablen bei einer beobachteten Person kann für sie die Basisrate um einen Faktor erhöht werden. Dieser wird folgendermassen bestimmt:
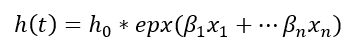
Das Modell liefert dafür die β-Koeffizienten. Aufgrund der Notwendigkeit, die linearen Modellkoeffizienten bei der Umrechnung in die Übergangsraten zu exponieren, wird das Modell auch oft Exponentialmodell genannt.
Ein positiver Koeffizient bedeutet einen positiven Einfluss der Kovariablen auf die Übergangsrate, ein negativer Wert impliziert einen negativen Einfluss. Wichtig dabei ist, dass die Verweildauer die Umkehrung der Übergangsrate ist! Eine kleinere Rate bedeutet also eine längere mittlere Prozessdauer und vice versa.
Überlebenszeitanalyse: Anforderung an Daten
Die Daten für eine Überlebenszeitanalyse sind in Episoden organisiert. Ein Proband kann dabei mehrere Episoden haben (zB. mehrere Arbeitsverhältnisse, Ehen, Krankheiten etc.). Zwei Informationen sind für die weiteren Analysen entscheidend, die Verweildauer der Episode und die Ereignisvariable:
- Verweildauer der Episode: Der genau Startzeitpunkt ist hier nicht notwendig, es sei denn, man möchte in weiterer Folge diesen kontrollieren.
- Ereignisvariable: Sie zeigt an, ob die Beobachtung mit einem Endereignis oder einer Zensierung endet.
Typischerweise kann nur die letzte beobachtete Episode einer Person zensiert sein. Diese Variable kann auch mehr als zwei Ausprägungen haben, wenn mehrere konkurrierende Zielzustände vorliegen (zB. Ende einer Ehe wegen Scheidung oder wegen Verwitwung).
Möchte man die Verweildauer bis zu einem bestimmten Zielzustand messen, dann werden die anderen Variablen/Ausprägungen als Zensierung behandelt. Die Daten können durch weitere Variablen zur Person oder zur Episode ergänzt werden, so wie im nachfolgenden Beispiel Geburtskohorte und Geschlecht.
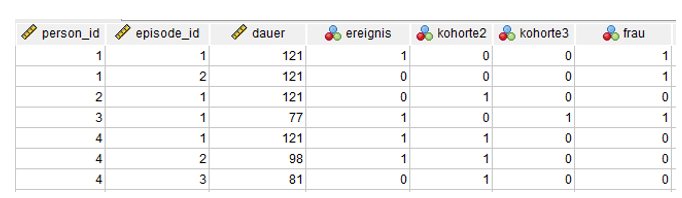
Cox Regression: Umsetzung in SPSS
Wir nutzen die oben gezeigten Daten, um die Umsetzung der Cox Regression in SPSS zu demonstrieren. In diesem Beispiel wird der Einfluss der Geburtskohorte und des Geschlechts auf die Vertragsdauer bei einem Mobilfunkanbieter, gemessen in Monaten ab dem Vertragsabschluss, untersucht.
In SPSS wählen wir: Analysieren –> Überleben –> Cox-Regression
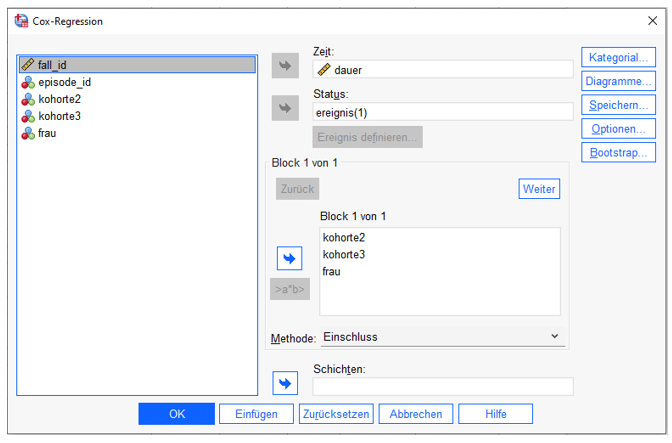
Im Feld ‘Zeit’ wählen wir zunächst unsere Variable dauer. Ins Feld ‘Status’ ziehen wir die Ereignisvariable und definieren die Ausprägung, die auf das untersuchte Ereignis (und nicht: Zensierung bzw. konkurrierende Zielzustände) hinweist.
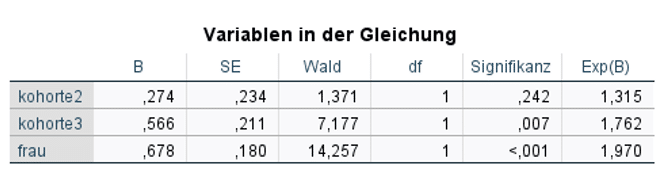
So sieht nun der für uns interessante Teil des Ergebnisoutputs aus. Der Koeffizient B zeigt die Wirkungsrichtung der unabhängigen Variablen auf die Übergangsrate an. Ein positiver Koeffizient bedeutet eine höhere Rate und damit kürzere Verweildauer.
Die Signifikanz des Wald-Tests zeigt zusätzlich, dass der Effekt von kohorte2 nicht signifikant, das heisst auf einem nicht akzeptablen Niveau von null verschieden ist. Die weiteren Effekte im Modell (kohorte3, frau) sind dagegen signifikant.
Durch das Exponieren des Koeffizienten (Exp(B)) berechnet das Programm das sogenannte hazard ratio. Damit kann ähnlich einem odds ratio die Stärke des Effekts beziffert werden. Hazard ratio zeigt an, um welchen Faktor die Übergangsrate bei einem Punkt Zunahme in der unabhängigen Variablen wächst.
Bei Dummy Variablen entspricht dem Vergleich zwischen abgebildeten und Referenzkategorien. Eine detaillierte Interpretation von hazard ratio fidnet sich einem früheren Beitrag.
Mithilfe des Felds ‘Diagramme’ läösst sich schliesslich die auf dem Modell basierte Überlebensfunktion berechnen. Ihre Interpretation ist analog einer Kaplan-Maier-Überlebenskurve. Interessant sind vor allem Gruppenvergleiche, wie hier am Beispiel des Geschlechts.
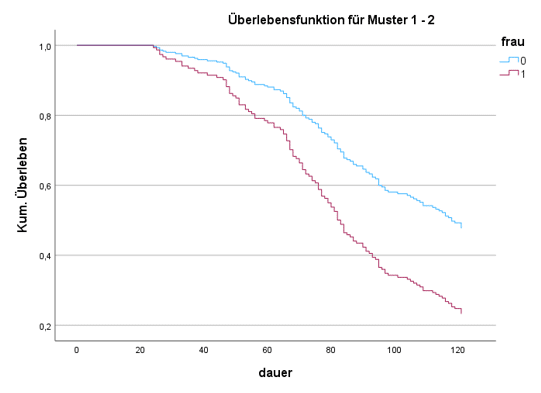
Hier zeigt die Grafik, dass der konstante Geschlechtereffekt auf die Übergangsrate zu einem immer grosser verwenden Abstand in Überlebensquoten führt. So haben nach 120 Monaten bereits 80 Prozent der Frauen, aber nur 50 Prozent der Männer ihren Vertrag gekündigt (Berechnung: (1 – Wert der Überlebensfunktion) * 100). Nach 40 Monaten beträgt der Abstand dagegen nur wenige Prozentpunkte.
Überlebensanalyse in SPSS: Fazit
Das Cox-Regression ist die erste Wahl bei einer Analyse von zeitlicher Prozessdauer bzw. Überlebensdauer. In SPSS lassen sich damit komplexe Zusammenhänge unter Berücksichtigung der spezifischen Datenstruktur mit Rechtszensierungen untersuchen.
In seiner Grundversion lässt sich das Modell sehr leicht im SPSS umsetzen und aussagekräftig interpretieren. Allerdings gibt es Forschungsdesigns, bei denen diese Grundversion nicht mehr ausreicht, etwa wenn
- man Variablen hat, die ihren Wert im Laufe des beobachteten Prozesses ändern (zeitabhängige Kovariablen)
- die Übergangsrate nicht zeitkonstant ist, sondern abschnittsweise konstant oder gar eine funktionale zeitliche Form besitzt.
Mit gewissen Anpassungen lassen sich diese Szenarien allerdings zumindest teilweise auch im SPSS umsetzen, allerdings haben Programme wie Stata oder R diesbezüglich deutlich besser entwickelte Anwendungen.
Fragen Sie dazu gerne beim erfahrenen Team von Novustat nach weiterführender Unterstützung und Hilfestellung bei der Arbeit mit unterschiedlichen Statistikprogrammen wie SPSS, Stata und R. Nutzen Sie dazu einfach das schriftliche Kontaktformular für ein unverbindliches Angebot!