Was haben selbst-fahrende Autos, „Smart Homes“ und die Börse gemeinsam? Richtig, es fallen im Verlauf der Zeit grosse Mengen an Daten an, die allesamt mit einer Zeitkomponente versehen sind. Daten mit einer Zeitkomponente nennt man auch Zeitreihe (Time Series), die Analyse dieser Daten entsprechend Zeitreihenanalyse. In der digitalisierten Welt werden Kenntnisse in diesen Bereichen immer wichtiger. Wir möchten diesem Guide deshalb die wichtigsten Grundlagen der Zeitreihenanalyse vermitteln. Unser Tutorial ist dabei anhand eines Beispiels verständlich erklärt – also quasi „Zeitreihenanalyse für Dummies“!
Dieser Artikel beantwortet folgende Fragen:
- Was ist eine Zeitreihe?
- Wie geht man bei der Analyse von Zeitreihen vor?
- Wie kann man zukünftige Werte einer Zeitreihe vorhersagen?
Einführung: Was ist eine Zeitreihe?
Am häufigsten ist eine Zeitreihe (oftmals auch „Time Series“) eine Sequenz von Datenpunkten, die zu aufeinanderfolgenden, gleich grossen Zeitpunkten erfasst wird (zum Beispiel jede Sekunde, jeden Tag oder jeden Monat). Die Analyse von Zeitreihen ist aufgrund des industriellen Bedarfs, insbesondere der Prognose von Nachfrage, Umsatz und Angebot von kommerzieller Bedeutung. Andere Beispiele für Zeitreihen sind die Höhe der Meeresgezeiten, die Anzahl der Sonnenflecken und der tägliche Schlusswert des Dow Jones Industrial Average. Oft verwendet man auch die Zeitreihenanalysen für Umsatzanalysen und Kostenanalysen.
Zeitreihenanalyse für Dummies – die wichtigsten Schritte
Wie in einem der vorherigen Tutorials über die Poisson-Regression wird in diesem Guide wieder ein Standard-R-Datensatz verwendet. Hierzu muss man zunächst das R-Paket „datasets“ importieren:
require(datasets)
Für diesen Guide werden wir den „USAccDeaths“ Datensatz verwenden. Dieser Datensatz beschreibt die Anzahl der Todesfälle durch Unfall in den USA von 1973 bis 1978. Wie so oft in der Datenanalyse beginnen wir mit einer Begutachtung der Time Series:
show(USAccDeaths)

Für die Zeitreihenanalyse ist es hilfreich, den Datensatz in einer R-Variable abzuspeichern. Das erreichen wir mittels
time_series = USAccDeaths
Grafische Analyse der Zeitreihe
Der in Abbildung 1 dargestellte Datensatz ist ziemlich unübersichtlich. Wir empfehlen daher in der Regel Zeitreihen über Liniendiagramme darzustellen. So sind Zusammenhänge (Trends und Saisonalitäten) häufig viel schneller zu erkennen. Dies erreichen wir mit dem R-Befehl
plot.ts(time_series)
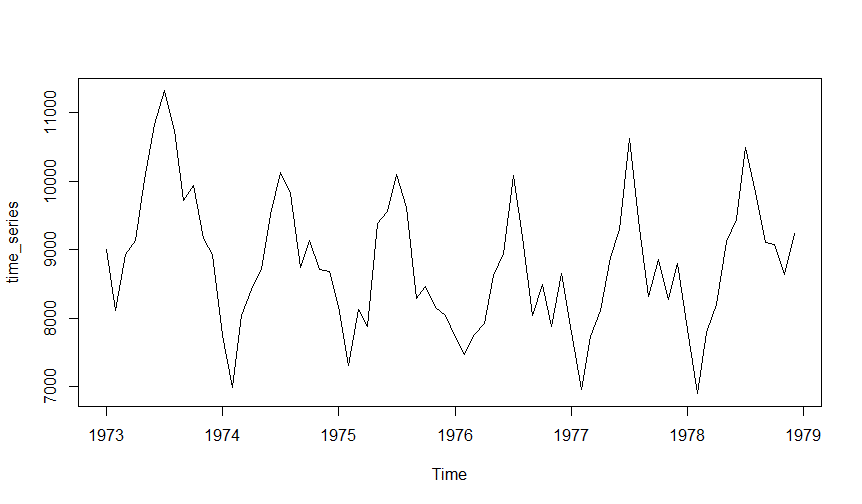
Der Graph ist bereits vielversprechend! Man kann schon erkennen, dass R die Zeitreihe richtig interpretiert, und auf der x-Achse die Jahreszahlen abträgt.
Komponenten einer Zeitreihe
Bevor der Plot genauer betrachtet wird, behandeln wir zunächst ein wenig Hintergrundwissen. Generell bestehen Zeitreihen aus den folgenden Komponenten:
- Trend, also wie entwickeln sich die Todesfälle „in der Tendenz“?
- Saisonale Komponenten: gibt es wiederkehrende Schwankungen in den Todesfälle, z.B. systematisch weniger Todesfälle zu Anfang eines Jahres?
- Fluktuationen (Zufällige Schwankungen): Möglicherweise treten z.B. zufällig und unsystematisch in einer Zeitspanne viele Todesfälle auf
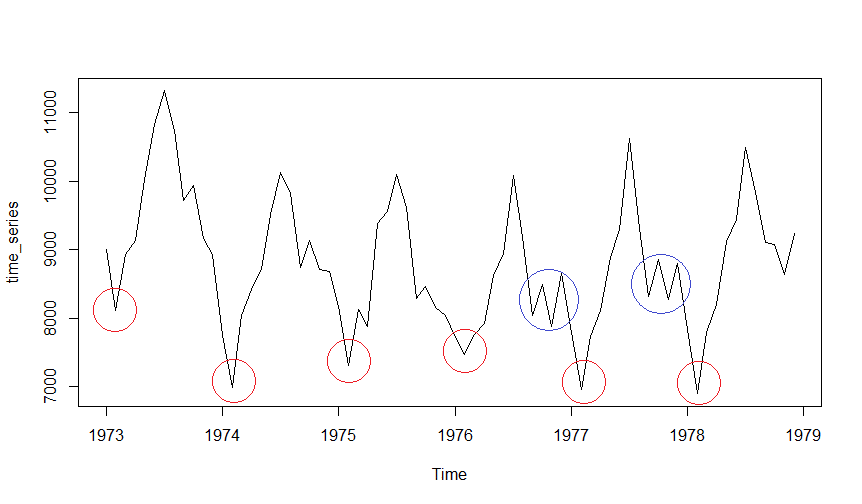
Was kann man nun im Plot genau erkennen? Scheinbar tritt immer zu Jahresbeginn ein Minimum auf (rote Kreise in der Abbildung oben). Dieses Phänomen ist, wie besprochen, Saisonalität. Wie man Saisonalität modelliert, ist zum Beispiel hier beschrieben. Abgesehen von diesen „groben“ Schwankungen gibt es auch „feinere“ Schwankungen (blaue Kreise in der Abbildung oben). Dies sind sogenannte Fluktuationen oder „weisses Rauschen“.
In R gibt es eine Funktion, mit deren Hilfe man Zeitreihen in die drei Komponenten Trend, Saisonalität und zufällige Fluktuationen aufteilen kann:
time_series_components <- decompose(time_series)
Der Rückgabewert time_series_components dieser Funktion enthält eine Liste, welcher verschiedene Komponenten enthält. Ein Plot dieser Liste zeigt Folgendes:
plot(time_series_components)
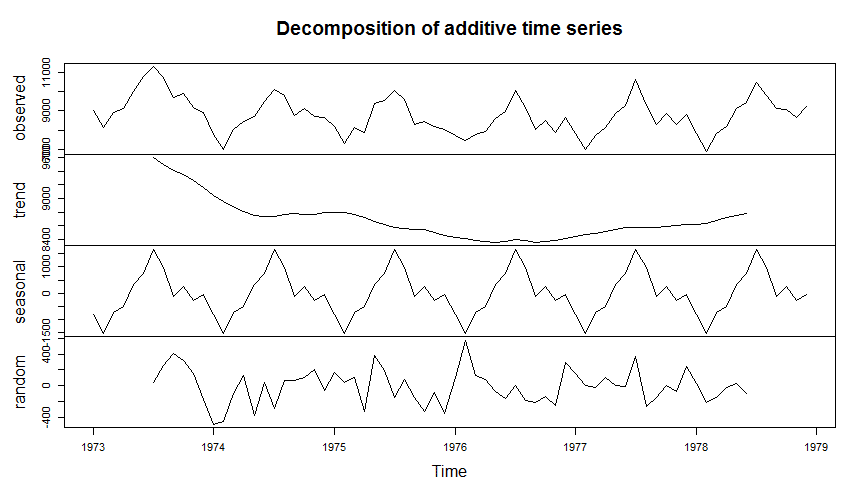
Die erste Zeile des Plots trägt zunächst die ursprüngliche Zeitreihe ab („observed“). In der zweiten Zeile („trend“) sieht man, wie die Todesfälle im Trend erst nach unten entwickeln und sich gegen Ende leicht erholen. In dieser Darstellung sind also saisonale und zufällige Komponenten „herausgerechnet“, diese finden sich in den Zeilen drei und vier des Plots („seasonal“ und „random“).
Zeitreihenanalyse für Dummies – Modellierungsverfahren
In vielen Business-Anwendungen mit Zeitreihen ist die Vorhersage ein essenzieller Bestandteil. Diese wird im Folgenden besprochen. Es wird wieder die Zeitreihe von Todesfällen benutzt:
time_series_vorhersage <- HoltWinters(time_series, alpha=0.1, beta=FALSE, gamma=FALSE)
Wie man sieht, wird die Methode von Holt-Winters (genauere Informationen über diese Vorhersagemethode finden sich hier) benutzt. Diese Methode ist in R bereits eingebaut. Wieder können wir das Ganze plotten:
time_series_vorhersage
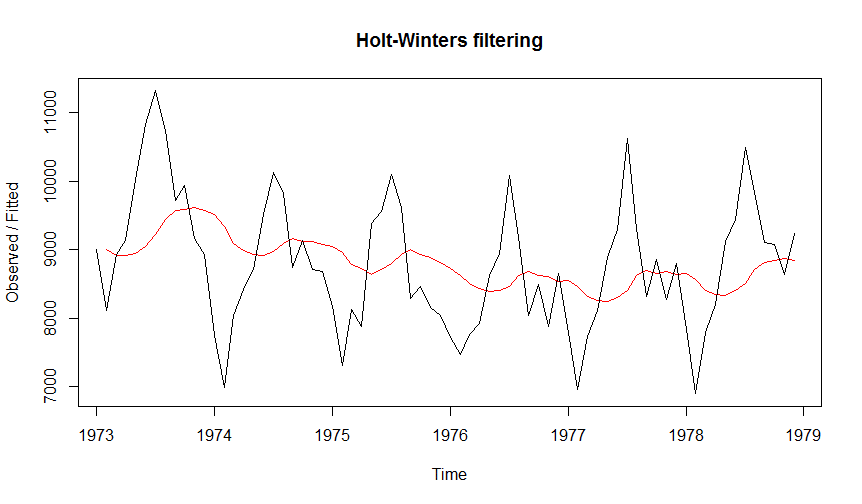
Der Plot zeigt zu jedem Zeitpunkt, was das Modell vorhergesagt hätte (auf Basis der Zeitreihe bis exakt VOR diesem Zeitpunkt).
Wie kommen nun Vorhersagen zustande? Um die Vorhersagen in R zu berechnen, benötigen wir noch die Bibliothek forecast. Falls diese nicht auf Ihrem System installiert ist, können Sie diese mittels install.packages(„forecast“) installieren.
library("forecast")
Jetzt können wir die Vorhersagen in R berechnen.
forecast:::forecast.HoltWinters(time_series, h=8)
Der Parameter h gibt hierbei die Anzahl der Zeitpunkte an, für die Vorhersagen gemacht werden (hier also 8).
Die Ausgabe hiervon lautet dann:
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
Jan 1979 8884.955 7663.197 10106.71 7016.438 10753.47
Feb 1979 8884.955 7657.103 10112.81 7007.118 10762.79
Mar 1979 8884.955 7651.040 10118.87 6997.845 10772.06
Apr 1979 8884.955 7645.006 10124.90 6988.617 10781.29
May 1979 8884.955 7639.002 10130.91 6979.434 10790.48
Jun 1979 8884.955 7633.026 10136.88 6970.294 10799.62
Jul 1979 8884.955 7627.078 10142.83 6961.199 10808.71
Aug 1979 8884.955 7621.159 10148.75 6952.146 10817.76
Zur Erinnerung: Unsere ursprüngliche Zeitreihe ging nur bis Dezember 1978. Hier sieht man also Vorhersagen für 8 Monate. Die hinteren Spalten geben sogenannte Konfidenzintervalle an – zum Beispiel ist im Januar 1979 der wahre Wert mit 95% Sicherheit zwischen 7016 und 10753 Todesfällen.
Fazit
Die Zeitreihenanalyse (Time Series Analysis) gewinnt in Zeiten von Big Data an Bedeutung und ist ein nützliches Tool in der statistischen Werkzeugkiste. Eine Zeitreihe enthält immer eine Zeitkomponente und lässt sich in Trend, Saisonalität und Zufallskomponente aufteilen. Es gibt verschiedene Vorhersagemodelle wie zum Beispiel die Methode von Holt-Winters, mit deren Hilfe zukünftige Werte vorhergesagt werden können.
Falls Sie weitere Fragen haben oder Hilfe bei Ihrem persönlichen Data-Mining-Projekt benötigen, können wir Ihnen jederzeit kompetent weiterhelfen.
