Jamovi ist ein kostenfreies sowie quelloffenes Statistik Programm und bietet eine vollwertige SPSS Alternative. Die Grundstruktur und allgemeinen Funktionsweisen haben wir im ersten Teil des jamovi Tutorials detailliert erläutert. Im zweiten Teil {Link] wurden umfassende Analysemöglichkeiten für deskriptive Statistik näher beleuchtet. Der dritte Teil widmet sich dem jamovi Tutorial für statistischer Tests wie etwa jamovi ANOVA.
Möchten Sie eigenständig oder mit Unterstützung von Expert*innen aussagekräftige statistische Analysen durchführen sowie Auswertungen mithilfe von jamovi umsetzen? Wenden sie sich hierzu gerne an uns für eine professionelle Statistik Beratung.
Analog zum Vorgehen bei deskriptiver Statistik nutzen wir für statistische Tests den Menü-Bereich “Analysen”: Die fünf (rechten) hier zur Verfügung stehenden Unterpunkte im Menübereich ermöglichen unterschiedliche statistische Tests. In diesem Artikel werden drei wichtige Testverfahren näher beschrieben, die sich mit dem Statistik Programm jamovi einfach und aussagekräftig umsetzen lassen. Dies sind: Kreuztabellen, Korrelation und Varianzanalyse (jamovi t-Test). In den nachfolgenden Beispielen wird der bereits aus Teil eins und zwei des Tutorials bereits TALIS-Fragebogen (mit fiktiven Daten) verwendet.
Jamovi Tutorial: Kreuztabellen
Die Kreuztabelle, umgesetzt durch den Chi-Quadrat Test – konkret Chi-Quadrat-Unabhängigkeitstest –, finden wir unter dem Menüpunkt “Häufigkeiten” aufgelistet. Dieses Testverfahren wird für nicht metrische, also kategoriale Variablen (nominal und ordinal) verwendet.
Der Begriff “Häufigkeiten” mag zunächst irreführend anmuten, das Symbol von vier Quadraten verdeutlicht aber sehr gut den Charakter einer Kreuztabellierung.
Grundlage aller statistischen Testverfahren ist ein Forschungsdesign mit Forschungsfrage und ausformulierten Hypothesen.
Im Beispiel wird konkret der Einfluss des Geschlechts als unabhängige Variable (UV) auf die Berufswahl (abhängige Variable) der Lehrkräfte untersucht. Es gilt also, statistisch die Frage nach der Unabhängigkeit der beiden Variablen voneinander zu testen. Für die Umsetzung empfiehlt es sich, neben den beobachteten Werten auch die erwarteten Werte sowie die Prozentwerte der UV – in diesem Fall die Zeilenprozentwerte – anzuklicken. Damit lässt sich eine detaillierte Analyse sowohl der Kreuztabelle als auch des Chi-Quadrat-Wertes (hier: 0,205) durchführen (Anmerkung: jamovi gibt Werte in der angloamerikanischen Schreibweise mit einem Punkt statt eines Kommas aus).
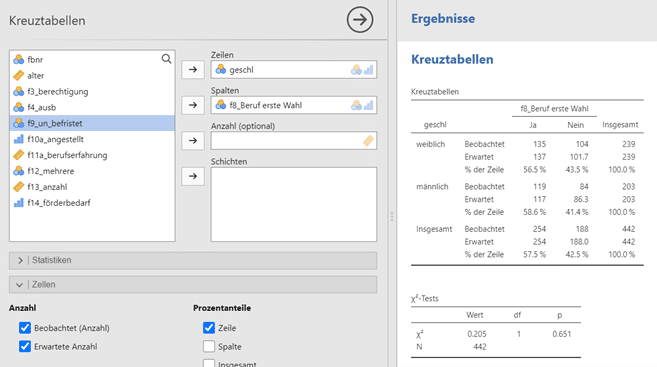
Die geringen Unterschiede in den Prozentwerten bei den Ausprägungen weiblich und männlich signalisieren bereits die Unabhängigkeit. Dies wird durch den (niedrigen) Chi-Quadrat-Wert von 0,205, der als Prüfgrösse die Differenz von beobachteten und erwarteten Werten in den Daten darstellt, widergespiegelt. Die erwarteten Werte sind hierbei theoretische Kennwerte für die Unabhängigkeit der einzelnen Variablenausprägungen. Je kleiner also der Chi-Quadrat-Wert ausfällt, desto unabhängiger sind die Variablen voneinander.
Schliesslich prüfen wir mittels p-Wert die Untersuchungshypothese. Dieser Wert liegt mit p = 0,651 deutlich über der 5-%-Grenze, somit wird die Nullhypothese beibehalten.
Jamovi Tutorial: Korrelation
Die Analyse der Korrelation ist unter dem Menüpunkt “Regression” zu finden, wir nutzen hier die Korrelationsmatrix. Dieses Testverfahren wird für metrische Variablen verwendet.
Im vorliegenden Beispiel testen wir den Einfluss des Alters auf die Berufserfahrung in Jahren. Bei beiden Variablen handelt es sich um metrisch skalierte Merkmale (auch sichtbar durch das Lineal-Symbol).
Die Umsetzung erfolgt analog den vorherigen Tests, bei den Korrelationskoeffizienten orientieren wir uns an Pearson’s r. Sollten die beiden Variablen allerdings nicht normalverteilt sein, dann wählen wir alternativ den Rangkorrelationskoeffizienten Spearman. Als Visualisierung liesse sich ergänzend noch ein Streudiagramm (scatterplot) darstellen, zu finden unter dem Menüpunkt “Exploration”.
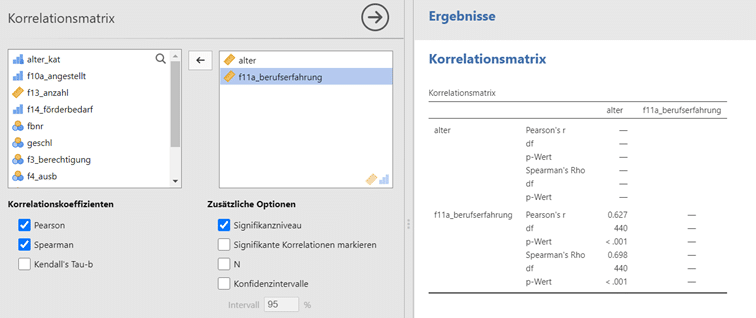
Der Ergebnisoutput rechts weist einen starken linearen positiven Zusammenhang zwischen den beiden Variablen auf (Wert über 0,6). Das lässt sich wie folgt interpretieren: je höher das Alter, desto mehr Berufserfahrung weisen die Lehrkräfte auf.
In Bezug auf den Hypothesentest zeigt sich ein p-Wert < 0,001, was auf einen signifikanten Zusammenhang zwischen Alter und Berufserfahrung schliessen lässt. Konkret besagt der Wert, dass die Wahrscheinlichkeit, sich zu irren, wenn man die Nullhypothese verwirft, bei unter 0,1 Prozent liegt.
Jamovi Tutorial: ANOVA
Als drittes Testverfahren soll abschliessend die univariate Varianzanalyse, konkret die einfaktorielle ANOVA im Menüpunkt “ANOVA” vorgestellt werden. Alternativ zur jamovi ANOVA eignet sich für kleine Stichproben und maximal zwei Variablenausprägungen auch der t-Test für unabhängige Stichproben. In diesem Testverfahren wird der Einfluss einer kategorialen UV auf eine metrische abhängige Variable getestet.
Im unterstehenden Beispiel prüfen wir konkret die Frage nach dem Einfluss des Alters auf die Berufserfahrung der Lehrkräfte in Jahren. Für die Analyse klicken wir zunächst die Überprüfung auf Homogenität (Levene Test) als wichtige Voraussetzung für die Durchführung der ANOVA an. Ergänzend können wir uns gegebenenfalls auch die Prüfung auf Normalverteilung anzeigen lassen.
Zusätzlich klicken wir die Tabelle mit Deskriptivstatistik an und eventuell die Diagrammdarstellung mit den Fehlerbalken.
Der Homogenitätstest weist einen Wert deutlich über 5 % aus, dies bestätigt die Homogenität der Varianzen der Variablen. Somit können wir für den Hypothesentest den sogenannten Fisher’s Test anwählen (bei ungleichen Varianzen würde alternativ der Welch’s Test durchgeführt).
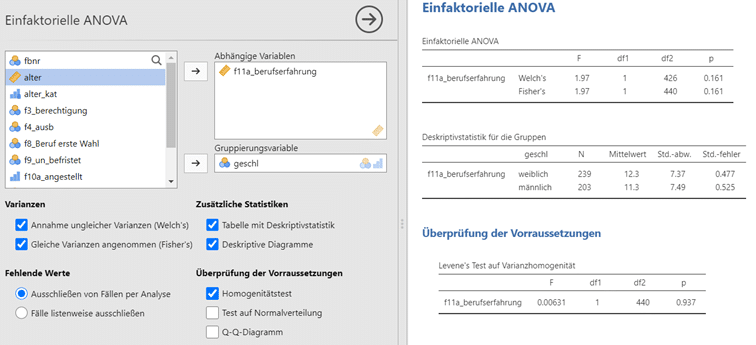
Das Ergebnis zeigt – auf Basis der nur geringen Unterschiede in den Mittelwerten von 11,3 Jahren bei Frauen und 12,3 Jahren bei Männern – einen p-Wert von 0,161. Dieser Wert liegt über der 5-%-Grenze, somit wird die Nullhypothese beibehalten und es lässt sich auf keinen signifikanten Einfluss des Alters auf die Berufserfahrung aller Lehrkräfte schliessen.
Fazit
Jamovi als kostenloses open source Statistik Programm bietet interessierten Nutzer*innen einen einfachen Zugang zu Analysen für deskriptive Statistik und statistische Tests. Ob jamovi ANOVA, Kreuztabelle oder Korrelation: Das dreiteilige jamovi Tutorial hat gezeigt, dass alle gängigen statistischen Tests einfach sowie schnell umsetzbar sind und jamovi eine qualitativ hochwertige SPSS Alternative darstellt.
Bei weiteren Fragen zu Programmierung, Auswertung und Interpretation, etwa für jamovi ANOVA, stehen Ihnen die Expert*innen von Novustat gerne zur Verfügung. Nutzen Sie dazu unverbindlich unser schriftliches Kontaktformular!