Bevor man eine univariate Varianzanalyse (ANOVA) durchführt, sollte man in jedem Fall die Voraussetzungen für diese Analyse prüfen. Ohne eine sorgfältige Prüfung der ANOVA Voraussetzungen sind Ergebnisse der Analyse möglicherweise ungültig. Signifikanztests können dann nicht zuverlässig interpretiert werden! Eine gründliche Überprüfung der Voraussetzungen für eine univariate Varianzanalyse ist aber glücklicherweise kein Hexenwerk. In diesem Artikel führen wir Schritt für Schritt durch den Voraussetzungen-Check für die Varianzanalyse. Zur Veranschaulichung werden wir dabei Beispiele in SPSS verwenden. So zeigen wir z.B., wie man zur Prüfung der Normalverteilung und Varianzhomogenität SPSS verwendet (Levene Test SPSS). Wenn Sie weitere Unterstützung zum Thema univariate Varianzanalyse benötigen, zögern Sie nicht unsere Statistik Hilfe in Anspruch zu nehmen!
Dieser Artikel beantwortet folgende Fragen:
- Welche ANOVA Voraussetzungen gibt es?
- Wann sind die Messungen unabhängig?
- Wie prüfe ich auf Normalverteilung?
- Wie verwende ich zur Prüfung der Varianzhomogenität SPSS (Levene Test SPSS)?
Univariate Varianzanalyse – Die Voraussetzungen auf einen Blick!
Im Wesentlichen gibt es 5 ANOVA Vorrausetzungen. Für einen ersten Überblick sind diese in der folgenden Tabelle dargestellt:
| Voraussetzung | Bedeutung | Prüfverfahren |
|---|---|---|
| Intervallskalierte abhängige Variable | Ist die abhängige Variable intervallskaliert? | (Geht aus Versuchsdesign hervor) |
| Kategoriale unabhängige Variable(n) | Sind alle unabhängigen Variablen nominalskaliert? | (Geht aus Versuchsdesign hervor) |
| Unabhängigkeit | Sind die Messwerte der Gruppen unabhängig voneinander? | (Geht aus Versuchsdesign hervor) |
| Normalverteilung | Ist die abhängige Variable für jede Gruppe in etwa normal verteilt? | Q-Q Diagramm Shapiro Wilk Test |
| Varianzhomogenität | Ist die Varianz für die abhängige Variable über alle Gruppen gleich? | Levene Test (SPSS) |
Im Folgenden werden wir auf jede dieser ANOVA Voraussetzungen im Detail eingehen.
Voraussetzung 1 – Intervallskalierte abhängige Variable
Zunächst geht eine univariate Varianz davon aus, dass die abhängige Variable intervallskaliert ist. Dies ist besonders häufig für die Auswertung von Fragebogen relevant: Die Antworten auf eine einzelne Frage sind nämlich häufig nur ordinal skaliert (wie z.B. bei einer Likert Skala). Daher sollten die Antworten auf eine einzelne Frage nicht als abhängige Variable für eine univariate Varianzanalyse verwendet werden. Mittelwerte aus mehreren Fragen verhalten sich dagegen annähernd intervallskaliert. Die abhängige Variable sollte in Fragebogen-Studien daher immer durch mehrere Fragen gemessen werden. Daher sollte man die geplante Analyse bereits bei der Gestaltung des Fragebogen Aufbau im Blick haben.
Voraussetzung 2 – Kategoriale unabhängige Variable(n)
Eine univariate Varianzanalyse vergleicht die Werte der abhängigen Variable über mehrere Gruppen. Daher sollten alle unabhängigen Variable natürlich auch Gruppen beinhalten. Alle unabhängigen Variablen sollten also kategorial sein. Ein Beispiel für eine ANOVA wäre etwa ein Vergleich der Geschmacksbewertung unterschiedlicher Tester für mehrere Eissorten. Die Geschmacksbewertung wäre dann eine intervallskalierte abhängige Variable. Die Eissorte wäre eine kategoriale unabhängige Variable. Denkbar wäre auch noch das Geschlecht der Tester als zweite kategoriale unabhängige Variable aufzunehmen. Wenn hingegen der Einfluss von kontinuierlichen Variablen (wie z.B. Alter) auf die abhängige Variable untersucht werden soll, bietet sich eventuelle eine lineare Regression als Alternative an.
Voraussetzung 3 – Unabhängige Messungen
Zu den ANOVA Voraussetzungen gehört die Annahme von unabhängigen Messungen. Häufig wird dieser Voraussetzung nur wenig Aufmerksamkeit geschenkt. Tatsächlich zählt diese Annahme aber mit Abstand zu den wichtigsten ANOVA Voraussetzungen! Selbst bei einer geringen Abweichung von dieser Annahme kann sich der Fehler 1. Art um ein vielfaches (!) vergrössern. Das bedeuten, dass das Signifikanzniveau α in Wirklichkeit um ein Vielfaches höher liegt als angenommen. Während man also möglicherweise glaubt ein Signifikanzniveau von α = 0,05 zu verwenden, liegt α möglicherweise tatsächlich bei 25%! In so einem Fall wäre jeder vierte “signifikante” Effekt in Wirklichkeit zufällig entstanden. Ergebnisse für so eine univariate Varianzanalyse wären also offensichtlich völlig unbrauchbar. Man sollte diese Voraussetzung also auf keinen Fall ignorieren!
Unabhängigkeit – Was bedeutet das jetzt genau?
Unabhängigkeit ist also wichtig – aber was bedeutet Unabhängigkeit der Messwerte genau? Bei unabhängigen Messwerten ist jeder Messwert unabhängig von anderen Messwerten zu Stande gekommen. Zur Verdeutlichung kommen wir auf unser Beispiel mit dem Geschmackstest zurück.
Nehmen wir an, wir möchten die Geschmacksbewertung verschiedener Tester für mehrere Eissorten vergleichen. Wenn jeder Tester genau eine Geschmacksbewertung abgibt, können wir im Regelfall von unabhängigen Messungen ausgehen. Problematisch wäre es aber, wenn jeder Tester mehrere Bewertungen abgibt – etwa für jede Sorte eine. Dann wären die verschiedenen Messungen von einem Tester nämlich abhängig voneinander. Wenn wir z.B. wissen, dass Tester 1 eine hohe Wertung für die Sorte Schoko und Zitrone abgegeben hat, können wir vermuten, dass die Wertung für Vanille auch eher hoch ausfällt. Dieser Tester wertet scheinbar Eis einfach allgemein höher. Die Bewertungen des Testers hängen also miteinander zusammen. Sie sind nicht unabhängig.
Probleme mit Unabhängigkeit treten für univariate Varianzanalyse häufig auf, wenn mehrere Messungen für dieselbe Person vorliegen (wie in unserem Beispiel). Dies ist besonders häufig bei Messungen über verschiedene Zeitpunkte der Fall. Ein typisches Beispiel wären medizinische Studien, die Patienten über mehrere Messzeitpunkte beobachten. Aber auch manche Gruppierungseffekte können zu abhängigen Beobachtungen führe. Dies kann beispielsweise bei einer Mitarbeiterbefragung über Zufriedenheit über mehrere Abteilungen der Fall sein: Wenn mehrere Mitarbeiter aus derselben Abteilung befragt werden, sind die Beobachtungen möglicherweise nicht unabhängig. Ein unzufriedener Mitarbeiter in einer Abteilung könnte die Stimmung für die gesamte Abteilung runterreissen. Andere Mitarbeiter wären dann also aufgrund dieses einen Mitarbeiters auch eher unzufrieden. Die Werte von Zufriedenheit innerhalb einer Abteilung hängen dann also voneinander ab und sind nicht unabhängig.
Was tun bei abhängigen Messwerten?
Bei abhängigen Messwerten kann eine Varianzanalyse mit Messwiederholung (repeated Measures) oder eine Mehrebenenanalyse (multilevel Model) sinnvoll sein. Unsere Experten von Novustat sind auch in der Anwendung solcher komplexer multivariater Verfahren erfahren – wir helfen ihn mit einer Statistik Beratung gerne weiter!
Voraussetzung 4 – Normalverteilung
Die univariate Varianzanalyse gehört zu den parametrischen Verfahren. Dies bedeutet, dass als Teil der ANOVA Voraussetzungen bestimmte Annahmen über die Verteilung der Daten gemacht werden. Bei einer ANOVA wird davon ausgegangen, dass die abhängige Variable in jeder getesteten Gruppe normal verteilt ist. Bevor man auf Normalverteilung kontrolliert, sollte man die Daten allerdings auf Ausreisser überprüfen. Dies kann beispielsweise durch einen SPSS Boxplot geschehen. Die Normalverteilung prüft man anschliessend am Besten über so genannte Q-Q Diagramme. Ergänzend kann man auch noch den Shapiro Wilk Test verwenden. Ähnlich wie beim Levene Test SPSS ist die Annahmenprüfung allein durch statistische Tests allerdings nicht ganz unproblematisch. Man sollte den Shapiro Wilk Test daher höchstens als Ergänzung zu Q-Q Diagrammen einsetzen.
In SPSS lässt sich beides über den Menüpunkt “Analysieren → Deskriptive Statistiken → Explorative Datenanalyse” anfordern. Die abhängige Variable wird dafür in das Feld “abhängige Variable” bewegt. Die zu analysierende Gruppe(n) werden als dann Faktoren festgelegt. Zusätzlich wählt man dann unter dem Menüpunkt “Diagramme” die Option “Normalverteilungsdiagramm mit Tests”.
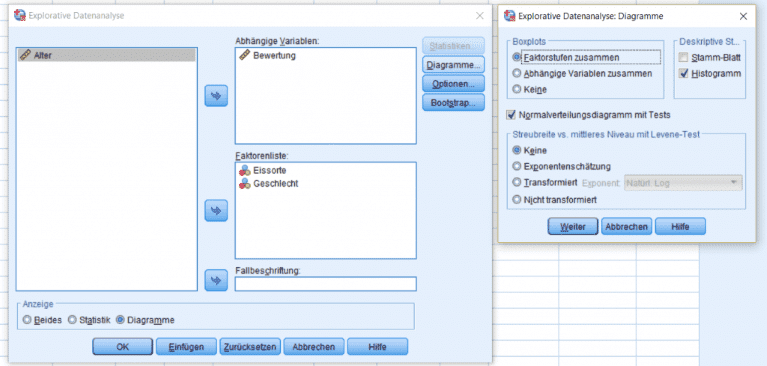
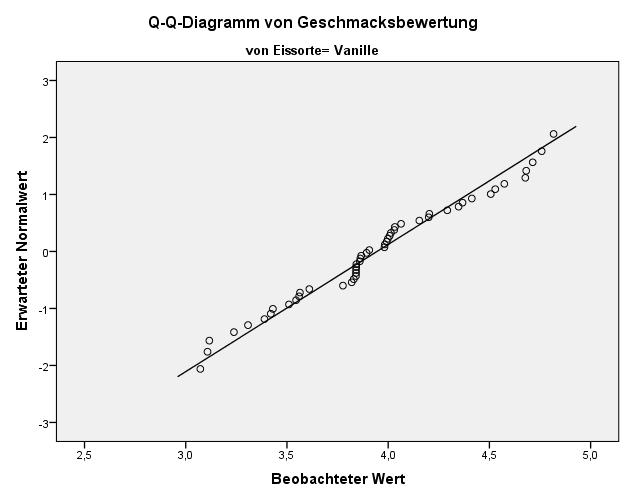
Bei einer (annähernden) Normalverteilung sollten die Beobachtungen in etwa der Diagonalen im Q-Q Diagramm folgen. Eine detaillierte Anleitung zur Prüfung der Normalverteilung findet sich in unserem Voraussetzungen-Check für parametrische Tests. Wenn die Normalverteilung verletzt sein sollte kann man versuchen die Daten zu transformieren oder auf nicht-parametrische Verfahren wie den Kruskal-Wallis-Test ausweichen.
Voraussetzung 5 – Varianzhomogenität (Levene Test SPSS)
Die letzte der ANOVA Voraussetzungen geht davon aus, dass die Varianzen über alle getesteten Gruppen gleich sind. Die Gleichheit der Varianzen wird bezeichnet man auch als Varianzhomogenität, SPSS liefert die benötigten Infos aber praktischerweise mit. Dafür muss man für die univariate Varianzanalyse lediglich die richtigen Kennzahlen anfragen. Für eine ANOVA wählt man zunächst in SPSS den Menüpunkt “Analysieren → Allgemeines lineares Modell → Univariat”. Dann wählt man die entsprechende abhängige Variable aus. Unabhängige kategoriale Variablen werden dem Feld “Feste Faktoren” zugeordnet. Um für die Prüfung der Varianzhomogenität SPSS zu verwenden, wählt man unter “Option” die Optionen “Deskriptive Statistiken” und “Homogenitätstest”.
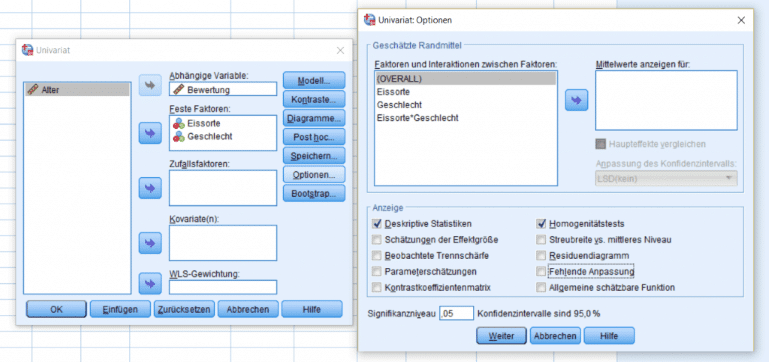
Mit Hilfe der Ausgabe für die univariate Varianzanalyse prüft man nun die Varianzhomogenität, SPSS liefert nun sowohl die Varianzen per Gruppe als auch den Levene Test (SPSS ordnet beide vor der eigentlichen ANOVA an).
Varianzhomogenität prüfen in SPSS: Beispiel
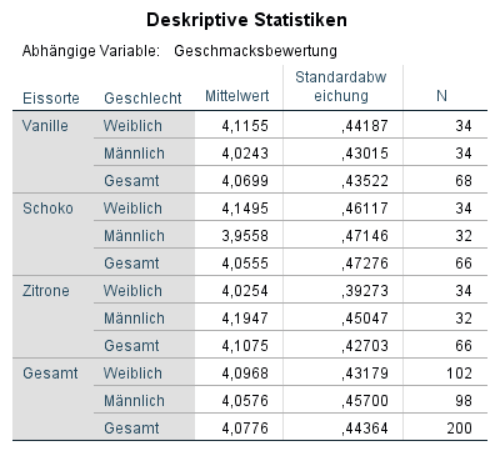
Man sollte zunächst die Gruppe mit der grössten Varianz mit der Gruppe der kleinsten Varianz vergleichen. Als Faustregel hat sich etabliert, dass die grösste Varianz nicht mehr als 1.5x grösser als die kleinste Varianz sein sollte. In unserem Beispiel ist die Gruppe mit der Grössten Varianz Zitrone & weiblich (Varianz = 0,39). Die Gruppe mit der kleinsten Varianz ist Schoko & männlich (Varianz = 0,47). Die grösste Varianz ist in etwa 1,21mal so gross wie die kleinste Varianz. Die Varianzhomogenität scheint also gegeben zu sein.

Der Levene Test SPSS bietet einen statistischen Test, um die Varianzen miteinander zu vergleichen. Um für die Überprüfung der Varianzhomogenität SPSS mit dem Levene Test SPSS zu verwenden, sollte man prüfen, ob der Test signifikant ausfällt. Bei einem signifikanten Ergebnis unterscheiden sich die Varianzen signifikant voneinander und die Varianzhomogenität ist nicht gegeben. In dem oben abgebildeten Beispiel wäre der Test nicht signifikant (F (5,194) = 0,14; p = 0,98). Die Varianzhomogenität scheint also gegeben zu sein. Wie oben bereits erwähnt haben formale Tests zur Prüfung von ANOVA Voraussetzungen (wie der Levene Test SPSS) allerdings einige Schwächen. Im Zweifelsfall sollte man daher der oben beschriebenen Faustformel den Vorrang geben. Der Levene Test (SPSS) sollte höchstens als Ergänzung zur manuellen Überprüfung eingesetzt werden.
Zusammenfassung: ANOVA Voraussetzungen überprüfen
Bevor man eine univariate Varianzanalyse durchführt, sollte man immer erst alle ANOVA Voraussetzungen gründlich prüfen. Nur so kann man sicher gehen, dass alle gewonnenen Erkenntnisse auch tatsächlich gültig sind. Darum haben wir in diesem Artikel demonstriert, wie man die ANOVA Voraussetzungen korrekt überprüft. Dabei haben wir auch gezeigt wie man für die Überprüfung mancher Annahmen wie Varianzhomogenität SPSS verwenden kann. Wir hoffen, Ihnen mit dieser Anleitung eine nützliche Hilfe für Ihre univariate Varianzanalyse geboten zu haben. Wenn Sie jedoch für Annahmeprüfung Ihrer Analyse oder darüber hinaus Statistik Hilfe benötigen, so zögern Sie nicht, unsere professionelle Hilfe anzufordern!