Die Wahl des richtigen statistischen Verfahrens ist nicht immer ganz einfach. Idealerweise haben Sie bereits klare Hypothesen formuliert und eine Vorstellung über das grundlegende statistische Verfahren. Aber selbst dann müssen Sie bei der Analyse noch entscheiden ob sie parametrische Tests verwenden möchten oder lieber auf einen nicht-parametrische Test zurückgreifen möchten. Die Entscheidung zwischen parametrischen Test oder nicht-parametrischen Test ist eine grundlegende Entscheidung für die statische Analyse. Darum wollen wir in diesem Artikel die Unterschiede zwischen den beiden Familien von statischen Verfahren erklären und Ihnen zeigen wie Sie sich für den richtigen Test entscheiden. Für eine tiefergehende Beratung zur Wahl und Durchführung des optimalen Verfahrens vereinbaren Sie ganz unkompliziert einen Termin zur Statistik Beratung bei uns!
Diese Fragen werden in diesem Artikel beantwortet:
- Wie unterscheiden sich parametrische Tests von einem nicht-parametrische Test?
- Welcher parametrische Test oder nicht-parametrische Test kommt für Ihr Projekt in Frage?
- Wie prüfen Sie die Voraussetzungen für einen parametrischen Test?
Parametrische Tests vs. nicht-parametrische Tests: Auf die Verteilung kommt es an
Parametrische und nicht-parametrische Tests bilden beide eine eigene Familie von verschiedenen statistischen Methoden. Wie alle statistischen Verfahren sind diese nur unter bestimmten Voraussetzungen gültig oder sinnvoll. So geht Pearson Korrelationskoeffizient r zum Beispiel davon aus, dass das beide analysierten Variablen kontinuierlich sind.
Parametrische Tests haben dabei alle eine Sache gemeinsam: Jeder parametrische Test geht davon aus, dass die Daten aus einer ganz bestimmten Verteilung stammen. Die meisten parametrischen Test gehen von einer Normalverteilung aus. Nehmen wir einen Vergleich von Performance-Ratings in einem Unternehmen von zwei unterschiedlichen Abteilungen. Ein möglicher parametrischer Test wäre hier der t-test. Dieser wäre aber nur zulässig, wenn die Ratings von beiden Abteilungen annähernd normal verteilt sind.
Dagegen haben nicht-parametrische Tests keinerlei Annahmen über die Verteilung der Daten. Diese Tests werden daher auch verteilungsfreie Tests genannt.
Parametrische Test: Vorsprung durch Power
Nicht-parametrische Tests sind also in mehr Situationen zulässig als parametrische Tests. Daher werden nicht-parametrische Tests auch als robuste Tests bezeichnet. Warum sollten Sie dann überhaupt parametrische Tests einsetzen? Schliesslich sind diese ja in weniger Situationen zulässig. Parametrische Tests gleichen diesen Nachteil allerdings dadurch aus, dass Sie eine grössere Teststärke oder auch Power als nicht-parametrische Tests haben. Mit anderen Worten: Wenn tatsächlich ein Effekt in der Population vorliegt, haben Sie mit einem parametrischen Test bessere Chancen diesen Effekt auch nachzuweisen.
Im Zweifel gilt deshalb: Wenn es die Verteilung der Daten zulässt, verwenden Sie einen parametrischen Test. Wenn die Verteilung der Daten aber den Annahmen eines parametrischen Tests widerspricht weichen Sie auf nicht-parametrische Tests aus.
| Vorteil | Nachteil | |
| Parametrische Tests | Grössere Teststärke – wenn Annahmen erfüllt | Geht von bestimmter Verteilung der Daten aus (meist Normalverteilung) |
| Nicht-parametrische Tests | Keine Annahmen über Verteilungen | Wenn Annahmen für parametrischen Test erfüllt: Geringere Teststärke |
Welcher statistische Test für welche Situation?
Für Ihre Datenanalyse sollten Sie also zunächst prüfen ob ein parametrisches Verfahren verfügbar ist und ob Ihre Daten über die benötigte Verteilung verfügen. Sollte dies nicht der Fall sein, können Sie immer noch auf ein nicht-parametrisches Verfahren ausweichen.
Einige häufig verwendeten Verfahren haben wir für Sie in der folgenden Tabelle dargestellt.
| Situation | Parametrischer Test | Nicht-parametrischer Test | Beispiel |
| 2 unabhängige Stichproben vergleichen | t-Test für unabhängige Stichproben | Mann-Whitney-U Test | Unterscheidet sich das Performance Rating von Abteilung A von Abteilung B? |
| 2 abhängige Stichproben vergleichen | t-Test für abhängige Stichproben | Wilcoxon-Test | Zeigen Mitarbeiter bessere Fähigkeiten in Excel nach einem Trainingskurs (Vergleich vor und nach Trainingskurs)? |
| 3+ unabhängige Stichproben vergleichen | Varianzanalyse (ANOVA / ANCOVA) | Kruskal-Wallis-Test | Welches der 4 Designs für unsere Webseite führt zu mehr Bestellungen? |
| 3+ abhängige Stichproben vergleichen | Varianzanalyse mit Messwiederholungen | Friedman-Test | Erhöht sich die Kaufabsicht für eines von 4 Autos nach einer Probefahrt (Vergleich vor und nach Trainingsfahrt)?
Unterscheidet sich der Effekt einer Probefahrt zwischen den 4 untersuchten Automodellen? |
| Zusammenhang zwischen 2 Variablen | Pearson-Korrelation | Kendalls Tau oder Spearman-Korrelation | Gibt es einen Zusammenhang zwischen der Arbeitsbelastung und Krankheitstagen? |
Natürlich gibt es natürlich noch eine Vielzahl weiterer parametrischer und nicht-parametrischer Test für spezielle Situationen. Sie sind unsicher, welches Verfahren für Ihr Forschungsprojekt das richtige ist? Wenden Sie sich doch einfach an unsere Experten für eine Statistik Beratung!
Der Voraussetzung-Check für Ihren parametrischen Test
Wenn Sie den idealen parametrischen Test für Ihre Hypothesen identifiziert haben, müssen Sie erst prüfen ob Ihre Daten über die benötigte Verteilung verfügen. Dabei gehen Sie in zwei Schritten vor.
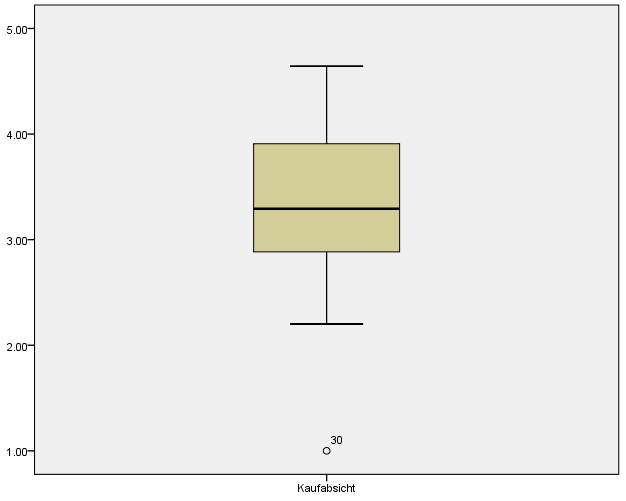
1 – Daten auf Ausreisser prüfen
Ausreisser verfälschen sehr schnell die Verteilung Ihrer Daten. Zudem sind auch einige nicht parametrische Verfahren anfällig gegenüber Ausreissern. Daher sollten Sie Ihre Daten in jedem Fall zuerst auf Ausreisser prüfen. Ausreisser können Sie dann gegebenenfalls von der weiteren Analyse ausschliessen. Wie Sie Ihre Daten korrekt auf Ausreisser überprüfen können Sie in unserem Artikel über Boxplots nachlesen.
2 – Verteilung überprüfen
Nun sind Sie bereit die Verteilung Ihrer Daten zu überprüfen. Die überwiegende Mehrheit parametrischer Tests geht von einer Normalverteilung aus. Daher zeigen wir Ihnen in diesem Artikel, wie Sie Ihre Daten auf die Normalverteilung prüfen. Einen ersten Eindruck über die Verteilung der Daten kann Ihnen natürlich ein Histogramm liefern. Ein Histogramm kann aber je nach Breite der Balken schnell einen verfälschten Eindruck liefern. Für eine korrekte Überprüfung verlassen Sie sich daher am Besten auf spezialisierte Methoden: Wenn Sie für den Test auf Normalverteilung SPSS verwenden gehören dazu vor allem der QQ-Plot, der Shapiro-Wilk Test und der Kolmogorov-Smirnov Test. Beide Verfahren können Sie in SPSS über den Menüpunkt „Deskriptive Statistiken Explorative Datenanalyse“ anfordern.
Für den QQ-Plot sollten die Datenpunkte in etwa der Geraden folgen. Weiterhin sollten die Tests auf Normalverteilung nicht signifikant ausfallen.

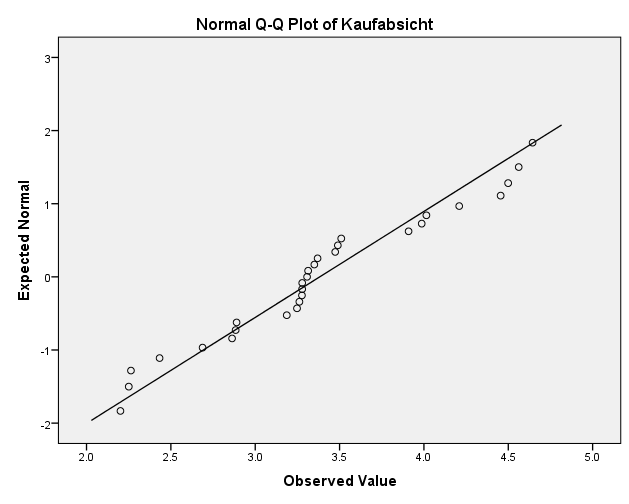
Um für den Test auf Normalverteilung SPSS korrekt zu verwenden empfehlen wir statistische Tests wie den Shapiro-Wilk Test nur in Kombination mit QQ-Plots zu verwenden. Der Test auf Normalverteilung mit formellen Tests weist als Verfahren nämlich einige Schwächen auf. Im Zweifelsfall sollten Sie dem visuellen Test mit QQ-Plot den Vorzug geben.
Sollte die Verteilung Ihrer Daten der Überprüfung stand halten, sind Ihre Daten annähernd normal verteilt. Solange alle übrigen Annahmen für den jeweiligen Test erfüllt sind, können Sie dann parametrische Tests wie z.B. den t-Test verwenden.
Test auf Normalverteilung SPSS: Daten sind nicht normal verteilt – was nun?
Wenn Ihre Daten deutlich von einer Normalverteilung abweichen sollten Sie zuerst eine Transformation der Daten in Erwägung ziehen. Transformationen wie die Wurzel- oder Log-Transformation können häufig dabei helfen, die nicht normale Daten einer Normalverteilung anzunähern. Dann können Sie anschliessend den parametrischen Test mit den transformierten Daten durchführen.
Wenn auch eine Transformation nicht ausreicht, hängt das weitere Vorgehen von der Grösse Ihrer Stichprobe ab. Bei grossen Stichproben sind parametrische Tests in der Regel robust gegenüber Abweichung von der Normalverteilung und ein parametrischer Test kann bei ausreichend grosser Stichprobe auch für nicht normale Daten verwendet werden. Für kleinere Stichproben sollten Sie jedoch auf nicht parametrische Tests ausweichen. Denn auch eine Datenanalyse mit nicht-parametrischen Tests kann zu wertvollen Erkenntnissen führen! Wenn Sie unsicher sind, wie Sie bei nicht normalen Daten vorgehen sollten können Sie sich auch mit unserer Statistik Hilfe Sicherheit verschaffen.
Parametrische Tests: Zusammenfassung
Sie kennen nun die Unterschiede parametrischer und einem nicht-parametrischer Tests ist und welche Vorteile ein parametrischer Test bietet. Wir haben Ihnen auch gezeigt, wie sie Ihre Daten auf Normalverteilung prüfen. Mit diesem Voraussetzung-Check können Sie entscheiden ob Sie einen parametrischen Test anwenden sollten. Wir hoffen, dass Ihnen dieser Text bei der Planung Ihrer Datenanalyse weitergeholfen hat. Falls Sie tiefergehendes Coaching zu statistischen Verfahren wünschen sollten, wenden Sie sich jederzeit an uns!
