In der inferenziellen Statistik (auch: schliessende Statistik) werden Hypothesen auf eine bestimmte Verteilung, auf einen Zusammenhang und auf einen signifikanten Unterschied innerhalb der betrachteten Merkmale getestet.
Ein Mediantest untersucht dabei zwei Stichproben auf einen signifikanten Unterschied ihrer Mediane, wobei der Wilcoxon-Test und der nach Mann und Whitney benannte U-Test SPSS verwendend als Standard gelten. Sie gehören zu den nicht- parametrischen Testverfahren und finden als Alternative zum t-Test Anwendung, wenn die Variablen bzw. Messungen als nicht annähernd normalverteilt angenommer werden können.
Im Folgenden werden die zu betrachtenden Fälle und die mathematischen Grundlagen der Testgrössen erklärt, bevor an Hand eines Beispiels Durchführung und Auswertung beschrieben werden.
Sollten Sie Unterstützung bei Ihrer Auswertung mit SPSS benötigen, helfen unsere Statistiker Ihnen gerne weiter. Nutzen Sie einfach unser Kontaktformular für eine kostenlose Beratung & ein unverbindliches Angebot – oder rufen Sie uns an.
Der Mediantest aus mathematischer Sicht
Zunächst sei daran erinnert, dass in der deskriptiven Statistik drei Messniveaus unterschieden werden: nominal, ordinal und metrisch (kardinal).
Die Mediantests Wilcoxon-Test und U-Test vergleichen die Abweichung der erhobenen Werte vom gemeinsamen Median der Stichproben. Da diese Abweichung mit exakt 50 Prozent-Wahrscheinlichkeit nach oben oder unten erfolgt, ist die Anzahl der abweichenden Werte binomialverteilt.
Auf Grundlage der Binomialverteilung müssen keine weiteren Annahmen für die Stichproben selbst getroffen werden, weshalb die Mediantests zu den nicht-parametrischen Testverfahren gehören.
Die genannten Mediantests unterscheiden sich nur in der Berechnung der Testgrösse, die eine eventuelle Verbindung der Stichproben berücksichtigt. Für die Messungen wird eine mindestens ordinale Skalierung benötigt.
Der Wilcoxon-Test: SPSS sinnvoll nutzen
Um für die Durchführung des Wilcoxon-Test SPSS zu nutzen, lassen sich zwei Pfade wählen. Dieser Mediantest untersucht zwei verbundene (gepaarte) Stichproben auf eine signifikante Abweichung ihrer Mediane. Dazu werden für jedes betrachtete Paar (Xi ; Yi) zunächst die absolute Differenz Yi-Xi und das Signum berechnet, sowie der Rang der Differenz ermittelt. Die gewichtete Summe dieser Grössen ergibt die Teststatistik.
Ist diese grösser als die Grenze des Konfidenzbereiches, kann die Nullhypothese verworfen und ein signifikanter Unterschied angenommen werden.
Dieser Mediantest kann in SPSS unter: „Analysieren → Nichtparametrische Tests“ gefunden werden, wobei zwischen einem geführten Dialog und der direkten Auswahl gewählt werden kann.
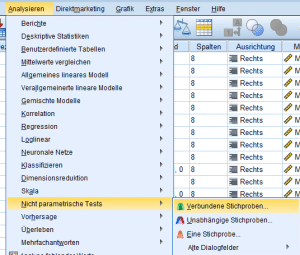
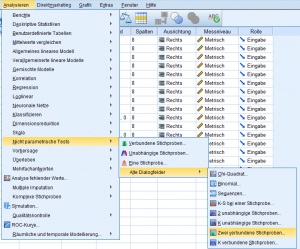
Im ersten Fall werden Nutzer durch den Auswahldialog geleitet und müssen die zu untersuchenden Stichproben für den Mediantest in SPSS anwendend auswählen.
Im zweiten Fall müssen lediglich die Stichproben aus der Liste gewählt werden.

Im folgenden Beispiel werden das Vertrauen der Befragten gegenüber dem Gesundheitswesen und dem Bundesverfassungsgericht miteinander verglichen. Die erste Tabelle listet die die gewichteten Rangsummen, die zweite die Signifikanz. Da diese deutlich unter 5% liegt, kann also angenommen werden, dass sich das dem Gesundheitswesen und dem Bundesfassungsgericht entgegengebrachte Vertrauen signifikant voneinander unterscheidet.
Der U-Test: SPSS sinnvoll nutzen
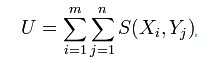
Für den U-Test SPSS nutzend stehen ebnfalls zwei Pfade zur Auswahl. Dieser Test untersucht zwei unverbundene Stichproben auf eine signifikante Abweichung ihrer Mediane. Dazu werden zunächst für beide Gruppen die Ränge der gesamten Umfrage ermittelt und innerhalb der Gruppen summiert.
Für jede Gruppe kann nun die jeweilige Statistik nach
ermittelt werden – der kleinere der beiden Werte wird als Mann-Whitneys U bezeichnet. Ist dieses grösser als die Grenze des Konfidenzbereiches, kann ein signifikanter Unterschied angenommen werden.
Der U-Test in SPSS ist unter dem Pfad: „ Analysieren → Nichtparametrische Tests“ zu finden, wobei zwischen einem geführten Dialog und der direkten Auswahl gewählt werden kann.
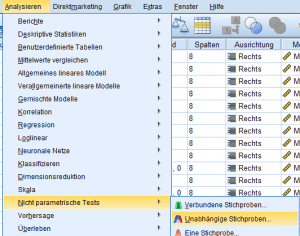
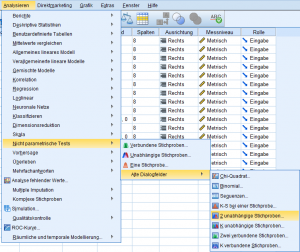
Im ersten Fall werden Nutzer durch den Auswahldialog geleitet und wählen die zu untersuchenden Stichproben für den U-Test SPSS anwendend aus.
Im zweiten Fall müssen lediglich die Stichproben aus der Liste gewählt werden, der U-Test in SPSS ist bereits voreingestellt.

Im folgenden Beispiel wurde die Wahlbeteiligung von Männern und Frauen untersucht, das nominale Merkmal „Geschlecht“ fungiert hierbei als unabhängige Gruppierungsvariable.
Nutzt man für den U-Test SPSS, so werden in der ersten Tabelle die Rangsummen und die Anzahl der Befragten der jeweiligen Gruppe angegeben, in der zweiten Tabelle der Wert der Teststatistik und die Signifikanz.
Da diese hier deutlich über 5% liegt, wird die Nullhypothese angenommen und es ist davon auszugehen, dass sich die Wahlbeteiligung männlicher und weiblicher Befragter nicht signifikant unterscheidet.
Praktische Anwendung von Mediantests in SPSS
Mediantests bieten eine wertvolle Alternative zu klassischen parametrischen Verfahren, insbesondere wenn die Annahme der Normalverteilung nicht erfüllt ist. In der statistischen Analyse werden sie häufig verwendet, um Unterschiede zwischen Gruppen oder Veränderungen über die Zeit hinweg zu untersuchen. SPSS stellt eine Vielzahl dieser Tests zur Verfügung, die sich je nach Datenstruktur und Untersuchungsziel gezielt einsetzen lassen. In den folgenden Beispielen zeigen wir, wie Mediantests in SPSS praktisch angewendet werden und welcher Test für welche Fragestellung geeignet ist.
1. Unterschiede zwischen Geschlechtern beim Einkommen
In einer Studie möchten wir herausfinden, ob es signifikante Unterschiede im Einkommen zwischen Männern und Frauen gibt. Da das Einkommen oft nicht normalverteilt ist, ist ein t-Test ungeeignet. Stattdessen eignet sich der Mann-Whitney-U-Test als Mediantest, da dieser keine Normalverteilung voraussetzt und zur Analyse von zwei unabhängigen Gruppen verwendet wird.
Warum dieser Test? Der Mann-Whitney-U-Test prüft, ob die Verteilungen in den beiden Gruppen gleich sind oder ob ein signifikanter Unterschied zwischen den Medians besteht. Dieser Test wird in SPSS unter „Nicht-parametrische Tests“ durchgeführt und eignet sich besonders für ordinalskalierte oder nicht-normalverteilte metrische Daten.
Durchführung in SPSS:
- In SPSS: Analyse > Nichtparametrische Tests > Zwei unabhängige Stichproben.
- Auswahl der Variablen „Geschlecht“ und „Einkommen“.
- Als Test „Mann-Whitney-U“ wählen.
2. Effekt eines Trainingsprogramms auf die Reduktion des BMI
In einem Experiment soll überprüft werden, ob ein spezielles Trainingsprogramm den BMI der Teilnehmer vor und nach dem Programm signifikant senken kann. Da der BMI nicht immer normalverteilt ist, wird hier der Wilcoxon-Vorzeichen-Rang-Test verwendet. Dieser Test vergleicht die Mediane zweier abhängiger Stichproben, was bei wiederholten Messungen notwendig ist.
Warum dieser Test? Dieser Mediantest ist eine Alternative zum t-Test für abhängige Stichproben und eignet sich, wenn die Daten nicht normalverteilt sind. Er vergleicht die Differenzen zwischen den Medians vor und nach der Intervention. Mit SPSS lässt sich dieser Test schnell und effizient durchführen.
Durchführung in SPSS:
- In SPSS: Analyse > Nichtparametrische Tests > Zwei verbundene Stichproben.
- Auswahl der Variablen „BMI vor“ und „BMI nach“.
- Als Test den „Wilcoxon-Vorzeichen-Rang-Test“ wählen.
Fazit
Die Wahl des richtigen Mediantests in SPSS hängt stark von der Anzahl der Gruppen und der Art der Daten ab. Der Mann-Whitney-U-Test wird bei zwei unabhängigen Gruppen verwendet und der Wilcoxon-Vorzeichen-Rang-Test bei abhängigen Stichproben. Mediantests sind besonders nützlich, wenn die Annahme der Normalverteilung nicht erfüllt ist, und können in SPSS leicht implementiert werden.
Häufig gestellte Fragen
Weiterführende Links
https://www.stat.auckland.ac.nz/~wild/ChanceEnc/Ch10.wilcoxon.pdf