Der t-Test in SPSS – Tests auf Unterschiede zweier Gruppen
In der inferenziellen Statistik (auch: schliessende Statistik) werden Hypothesen auf eine bestimmte Verteilung, auf einen Zusammenhang und auf einen signifikanten Unterschied innerhalb der betrachteten Merkmale getestet.
Bei der Auswahl t-Test SPSS ist zudem zwischen parametrischen und nicht-parametrischen Verfahren zu unterschieden, wobei der t-Test SPSS gestützt auf dem bekannten parametrischen Mittelwerttest nach Student basiert mit der Annahme, dass die untersuchte Variable annähernd normalverteilt ist.
Im Anschluss werden die theoretischen Grundlagen des t-Test -SPSS hat drei Varainten implementiert- vorgestellt. Abschliessend werden diese an Hand eines Beispiels erläutert.
Sollten Sie Unterstützung bei Ihrer Auswertung mit SPSS benötigen, helfen unsere Statistiker Ihnen gerne weiter!
Parametrische Tests – der t-Test allgemein
Wiederholend soll vorab an die drei in der deskriptiven Statistik unterschiedenen Messniveaus erinnert werden: nominal, ordinal und metrisch (kardinal).
Bei metrischen Merkmalen kann die empirische Verteilungsform ermittelt werden, die sich gemäss dem Gesetz der grossen Zahlen mit zunehmender Stichprobengrösse der tatsächlichen Verteilung in der Population annähert. Ist diese Näherung für eine angenommene Normalverteilung hinreichend gut, kann der t-Test durchgeführt werden.
Da für eine Normalverteilung sowohl der Mittelwert als auch die Standardabweichung bekannt sein müssen, entwickelte William S. Gosset 1908 unter dem Pseudonym Student die t-Verteilung (auch: Student-Verteilung), die auch bei unbekannter Standardabweichung den Test ermöglicht.
Für ein oder mehrere kardinal skalierte Merkmale vergleicht der t-Test die Abweichung der Mittelwerte voneinander – wahlweise zweier Merkmale voneinander oder eines Merkmals zu einem gegebenen Wert. Übersteigt diese den ermittelten Konfidenzbereich, kann der Unterschied als signifikant angenommen werden.
Im Folgenden gehen wir auf die Durchführung des t-tests in SPSS ein.
Sie möchten den t-Test oder eine andere Statistik durchführen, sind aber unsicher, wie dieser korrekt angewandt wird? Wir bieten professionelle Unterstützung für Ihre statistische Auswertung! Nutzen Sie einfach unser Kontaktformular für eine kostenlose Beratung & ein unverbindliches Angebot – oder rufen Sie uns an.
Der t-Test: SPSS-Anwendung
Um für den t-Test SPSS zu nutzen, folgt man dem Reiter: „Analysieren → Mittelwerte vergleichen“
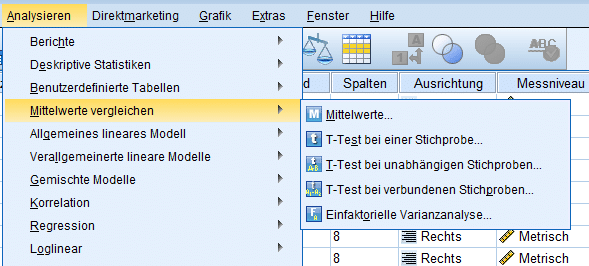
Beim t-Test in SPSS werden drei Fälle unterschieden:
- eine Stichprobe – hierbei wird untersucht, ob der Mittelwert eines gemessenen Merkmals signifikant von einem vorgegebenen Wert abweicht.
- unabhängige Stichproben – hierbei wird untersucht, ob sich die Mittelwerte zweier Gruppen, die einander nicht beeinflussen, signifikant voneinander unterscheiden. Als Beispiel dient hier das Einkommen männlicher und weiblicher Befragter, da die Gruppeneinteilung nach Geschlecht disjunkte Mengen bildet.
- verbundene (gepaarte) Stichproben – hierbei wird getestet, ob sich die Mittelwerte zweier verbundener Gruppen signifikant voneinander unterschieden, z.B. der Puls einer Testgruppe vor und nach Einnahme eines Medikaments
Fall 1: t-TEST SPSS mit einer Stichprobe:
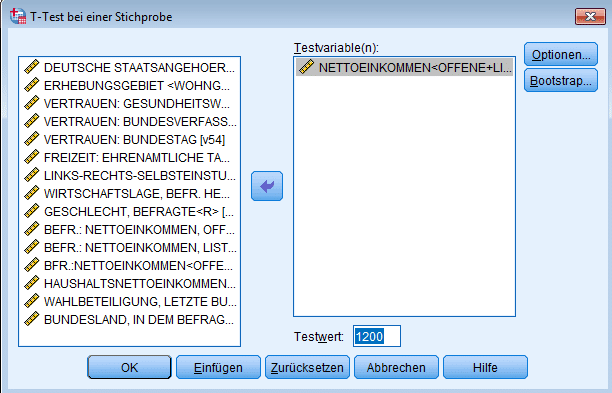
Zunächst werden die zu testenden Variablen aus der Liste gewählt, in unserem Beispiel das Nettoeinkommen, und dann der Testwert vorgegeben. Im Beispiel wird getestet, ob sich das Nettoeinkommen der Befragten signifikant vom Wert 50.000€ pro Jahr unterscheidet.

Der Mittelwert von 35.714,65 liegt unterhalb der vorgegebenen 50.000, die Signifikanz von weniger als 5% gibt zudem an, dass die Abweichung nach unten als signifikant angenommen werden kann.
Fall 2: t-TEST SPSS mit zwei unabhängigen Stichproben:
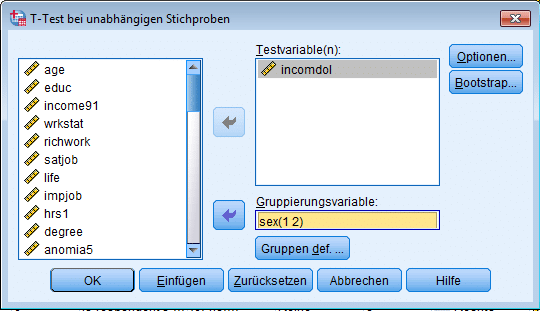
Im Falle zweier unverbundener Stichproben wird zuerst die kardinal skalierte zu untersuchende Variable aus der Liste gewählt, danach die beliebig skalierte Gruppierungsvariable. Bevor der t-Test in SPSS ausgeführt wird, sind die (beiden) Ausprägungen der Gruppe noch zu definieren.
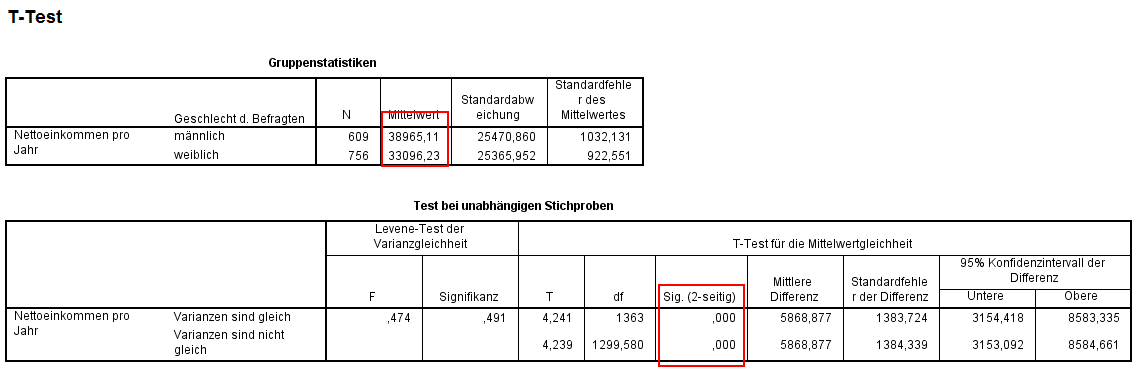
Für den t-Test SPSS nutzend, legen die in der ersten Tabelle zu findenden Mittelwerte nahe, dass männliche Befragte im Mittel mehr verdienen als weibliche Befragte. Da die Signifikanz in der zweiten Tabelle unter 5% liegt, kann der Unterschied als signifikant für die Population angenommen werden.
Vor der Interpretation der Signifikanz muss noch der Test auf Varianzhomogenität mittels Levene-Test durchgeführt werden. Die Nullhypothese testet hier, ob die Varianzen in beiden Gruppen annähernd gleich sind. Ist der p-Wert nicht signifikant, also grösser als 5%, dann ist Varianzhomogenität gegeben. Andernfalls sind die Varianzen nicht gleich. Hier liefert SPSS Ergebnisse zum Levene-Test für beide Fälle, für die Interpretation wird dann einfach der Wert in der entsprechenden Zeile verwendet.
Fall 3: t-TEST SPSS mit zwei verbundenen (gepaarten) Stichproben:
Zwei verbundene (gepaarte) Stichproben liegen vor, wenn die gleiche Stichprobe zu zwei aufeinander folgenden Messzeitpunkten befragt wird, z.B.: Frage nach Unterschieden in der wöchentlichen Arbeitszeit mit und ohne Partner.
Die beiden metrischen Variablen werden aus der Liste ausgewählt, die Reihenfolge spielt dabei keine Rolle.
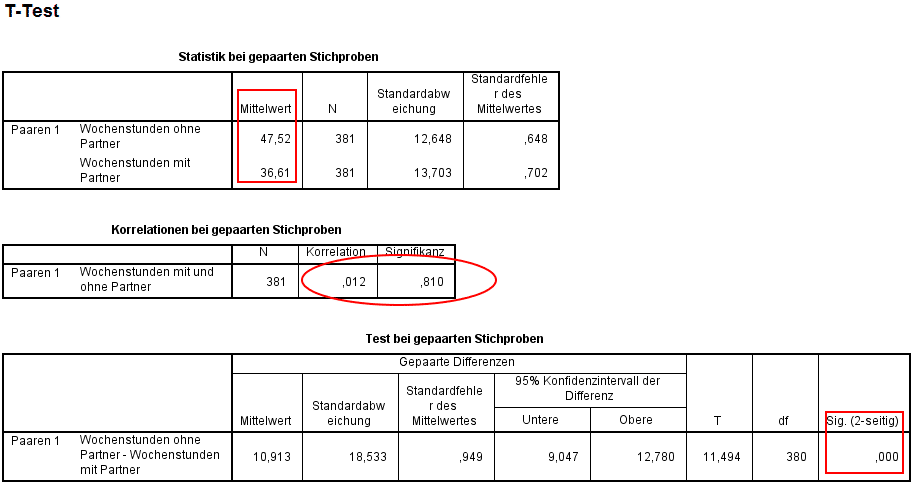
Der ersten Tabelle können wieder die Mittelwerte der beiden Merkmale entnommen werden, welche nahelegen, dass die Befragten nach dem Ende einer Beziehung mehr Zeit in der Arbeit verbringen als bei Bestehen der Beziehung.
Die in der dritten Tabelle ermittelte Signifikanz von weniger als 5% lässt diesen Unterschied als signifikant für die gesamte Population annehmen.
Ergänzend wird beim t-Test SPSS anwendend im Falle von zwei verbundenen Stichproben noch der Korrelationskoeffizient ermittelt.