Die Auswahl des korrekten statistischen Tests spielt beim Vergleich von zwei Stichproben eine entscheidende Rolle. Deshalb müssen die vorliegenden Daten genau betrachtet werden. Neben deren Verteilung, Skalen und Stichprobenumfang spielt dabei auch eine Rolle, ob diese “gepaart” erhoben wurden. Hier erklären wir, was gepaarte Daten sind und unter welchen Voraussetzungen der Wilcoxon Vorzeichen Rang Test die richtige Wahl ist. Die Anwendung des Wilcoxon Test wird beispielhaft in R dargestellt.
Sie benötigen Unterstützung bei der Analyse Ihrer Daten? Gerne unterstützen wir Sie in Form eines persönlichen Coachings. Wenden Sie sich hierzu an uns und unsere Expert*innen für eine Statistik Beratung!
Was sind eigentlich gepaarte Daten?
Möchten wir beispielsweise wissen, ob Personen montags oder freitags motivierter zur Arbeit kommen, lässt sich dieses Problem auf zwei verschiedene Weisen betrachten: Einerseits können wir zwei zufällige Stichproben von Arbeitnehmer*innen befragen, wobei die eine Gruppe montags und die andere Gruppe freitags zu ihrer Motivation befragt wird. Hierbei handelt es sich dann um unabhängige oder auch ungepaarte Stichproben.
Andererseits können wir dieselben Personen einmal am Montag und einmal am Freitag befragen und die jeweiligen Werte direkt miteinander vergleichen. In solch einem Fall liegen gepaarte Daten vor: Jeder Wert der einen Gruppe kann eindeutig einem Wert der anderen Gruppe zugeordnet werden. Häufig handelt es sich dabei um Messwiederholungen, aber auch andere Paarungen sind denkbar, wie z. B. die Grösse des linken und des rechten Fusses derselben Person.
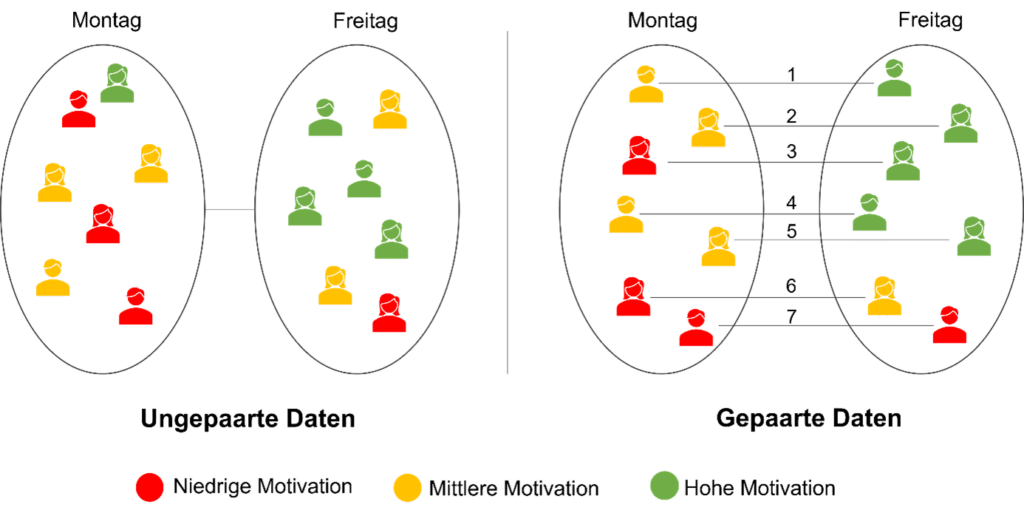
Ein weiterer Unterschied besteht in der Struktur der Daten, die sich aus der Art der Erhebung ergibt. Bei ungepaarten Daten werden diese meist in einer gemeinsamen Variable abgelegt, während eine zusätzliche Variable die Zuordnung zu den Gruppen dokumentiert. Gepaarte Daten finden sich hingegen meist aufgeteilt in zwei Variablen (z. B. 1. Messung und 2. Messung), wobei die jeweiligen Paare in einer Zeile stehen.
T-Test für abhängige Stichproben oder Wilcoxon Vorzeichen Rang Test?
Nachdem klar ist, dass Daten aus zwei gepaarten Stichproben vorliegen, müssen wir den richtigen statistischen Test auswählen. Folgen die Daten einer metrischen Skala (z. B. Gewicht, Grösse, Gehalt) und die Differenzen der gepaarten Werte einer Normalverteilung (nach Shapiro-Wilk), können wir auf den t-Test für gepaarte Stichproben (auf Englisch: paired samples t-Test) zurückgreifen. Allerdings lässt sich dieser Test für das oben genannte Beispiel nicht verwenden, da die gemessene Variable nicht metrisch, sondern ordinal skaliert ist.
Obwohl Daten auf einer Ordinalskala in eine Rangfolge gebracht werden können (z. B. niedrige Motivation – mittlere Motivation – hohe Motivation), muss der Abstand zwischen Rangplatz 1 und 2 nicht immer das Gleiche bedeuten wie zwischen Rangplatz 2 und 3. Dies ist häufig bei Umfragen der Fall (siehe auch: Likert-Skala).
Daher ist bei solchen Beispielen der Wilcoxon Vorzeichen Rang Test (manchmal auch kurz nur “Wilcoxon-Test”, auf Englisch: Wilcoxon signed-rank test) die richtige Wahl. Dieser ist zudem anwendbar, wenn die Differenzen der Paare nicht normalverteilt sein sollten. Zudem kann eine weitere Herausforderung darin bestehen, dass sich die Normalverteilung bei kleinen Stichproben (n ≤ 30) nicht sinnvoll überprüfen lässt. Auch hier ist der Wilcoxon Vorzeichen Rang Test eine sichere Wahl.
Anwendungsbeispiel: Der Wilcoxon Vorzeichen Rang Test in R
Fragestellung und Datenaufbereitung
Nun wollen wir die Durchführung des Wilcoxon Vorzeichen Rang Tests in R demonstrieren und bleiben dafür bei dem Beispiel zur Arbeitnehmer*innen-Motivation.
Fragestellung: Gibt es einen Unterschied zwischen der Motivation der Arbeitnehmer*innen am Montag und der Motivation am Freitag?
Damit werden folgende Hypothesen untersucht:
H0: Es gibt keinen Unterschied zwischen der Motivation am Montag und am Freitag.
H1: Es gibt einen Unterschied zwischen der Motivation am Montag und am Freitag.
Für die Berechnung müssen die Angaben zur Motivation zunächst in eine Ordinalskala übersetzt werden:
| Niedrige Motivation | 1 |
| Mittlere Motivation | 2 |
| Hohe Motivation | 3 |
Bezogen auf die obige Abbildung, ergibt sich damit folgendes Zahlenbeispiel:
| ID | Motivation am Montag | Motivation am Freitag | Differenz |
| 1 | 2 | 3 | + 1 |
| 2 | 2 | 3 | + 1 |
| 3 | 1 | 3 | + 2 |
| 4 | 2 | 3 | + 1 |
| 5 | 2 | 3 | + 1 |
| 6 | 1 | 2 | + 1 |
| 7 | 1 | 1 | 0 |
Der Wilcoxon Vorzeichen Rang Test betrachtet nun die Differenzen, indem diese zunächst sortiert werden und anschliessend jeder Differenz ein Rang zugeordnet wird. Bei gleichen Differenzen erhält jede den durchschnittlichen Rang der jeweils gleichen Differenzen.
| ID | Motivation am Montag | Motivation am Freitag | Differenz | Rang |
| 3 | 1 | 3 | + 2 | 1 |
| 1 | 2 | 3 | + 1 | 4 |
| 2 | 2 | 3 | + 1 | 4 |
| 4 | 2 | 3 | + 1 | 4 |
| 5 | 2 | 3 | + 1 | 4 |
| 6 | 1 | 2 | + 1 | 4 |
| 7 | 1 | 1 | 0 | 7 |
Nach Einlesen des Datensatzes in R betrachten wir zunächst die Mediane der beiden Variablen. Montags liegt der Median bei 2 (mittlere Motivation), während freitags im Median eine hohe Motivation (= ein Medianwert von 3) vorliegt.

Ungerichtete Hypothesenprüfung
Anschliessend wollen wir diesen Unterschied statistisch überprüfen. Dafür installieren und laden wir zunächst (einmalig) das Paket exactRankTests. Der Befehl für den Wilcoxon Vorzeichen Rang Test in R lautet wilcox.exact(x, y, paired = TRUE), wobei x und y die Daten der zu vergleichenden Stichproben sind (der ebenfalls häufig verwendete wilcox.test(x, y, paired = TRUE) kann bei gleichen Rängen und fehlenden Unterschieden keinen exakten p-Wert berechnen und liefert daher andere Ergebnisse).
Ausserdem besteht die Möglichkeit, mithilfe des Befehls alternative = c(“two.sided”, “less”, “greater”) anzugeben, ob der Wilcoxon Test ein- oder zweiseitig erfolgen soll. Ein zweiseitiger Test ist dann sinnvoll, wenn ein genereller Unterschied zwischen Werten zweier Stichproben analysiert werden soll, aber nicht, welche Richtung dieser annimmt (z. B. die Motivation der Arbeitnehmer*innen ist freitags höher als montags).

Die Teststatistik V gibt die Rangsumme an (hier V = 5*4 + 1 = 21), ist aber nicht direkt interpretierbar. Sie wird von dem R-Paket genutzt, um auf Basis der Differenzen und des Stichprobenumfangs einen p-Wert zu berechnen. Da der p-Wert ist kleiner als 0,05 ausfällt (in diesem Fall 0,031), können wir einen signifikanten Unterschied in der Motivation der Arbeitnehmer*innen annehmen.
Gerichtete Hypothesenprüfung
Wurde vor Durchführung des Wilcoxon Test bereits die Hypothese aufgestellt, dass die Motivation der Arbeitnehmer*innen am Freitag stets höher als am Montag ausfällt, ist auch ein einseitiger Test möglich. Hier muss im Rahmen des Befehls alternative = “greater“ angegeben werden (bzw. alternative = “less“, sollte die Vermutung gegenteilig lauten).
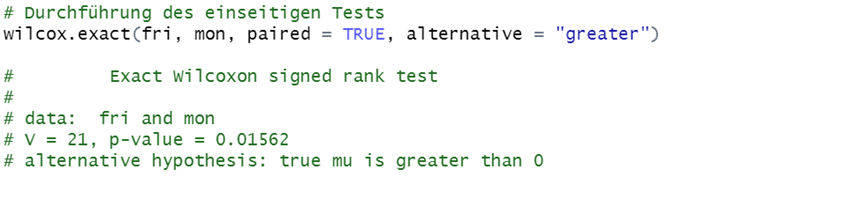
Nach der Durchführung des einseitigen Tests ist der p-Wert ebenfalls signifikant, da der Wert mit p = 0,016 unterhalb des Signifikanzniveaus (für einseitiges Testen) von 0.025 liegt. Wir können in diesem Beispiel also die Alternativhypothese annehmen, dass Arbeitnehmer*innen am Freitag signifikant motivierter sind als am Montag.
Achtung: Der Wilcoxon Vorzeichen Rang Test darf nicht mit dem Wilcoxon Rangsummentest (auf Englisch: Wilcoxon rank-sum test) verwechselt werden. Letzterer ist auch als Mann-Whitney-U-Test bekannt, vergleicht zwei Stichproben von ungepaarten Daten und kann somit als Alternative zum t-Test für unabhängige Stichproben betrachtet werden.
Fazit
Der Wilcoxon Vorzeichen Rang Test ist eine nichtparametrische Alternative zum gepaarten t-Test und kann somit auch auf gepaarte Daten angewendet werden, die ordinal skaliert oder deren Differenzen nicht normalverteilt sind. In R kann man mit einem einfachen Befehl testen, ob es signifikante Unterschiede zwischen den gepaarten Gruppen gibt.
Sollten Sie Bedarf an einer professionellen Hilfeleistung z. B. im Rahmen der Umsetzung in R oder anderen Statistikprogrammen wie SPSS oder Stata haben, zögern Sie nicht und kontaktieren Sie uns! Nutzen Sie dazu gleich und unverbindlich unser schriftliches Kontaktformular!
Weiterführende Links
Frank Wilcoxon: Individual Comparisons by Ranking Methods. In: Biometrics Bulletin. Band 1, Nr. 6, 1945, S. 80–83. https://www.jstor.org/stable/3001968
Jürgen Bortz, Gustav A. Lienert, Klaus Boehnke: Analyse von Rangdaten. In: Verteilungsfreie Methoden in der Biostatistik. 2008, S. 197-294. Springer, Berlin, Heidelberg. https://link.springer.com/chapter/10.1007/978-3-540-74707-9_6