Was bedeutet normalverteilt?
Die Normalverteilung (auch Gauss-Verteilung oder Gausssche Normalverteilung genannt) ist die wichtigste Wahrscheinlichkeitsverteilung und nimmt bei nahezu allen statistischen Analysen eine tragende Rolle ein. So wenden wir in der Praxis die Normalverteilung in zahlreichen Datenauswertungen für unsere Kunden an. Aber was bedeutet normalverteilt genau? In diesem Artikel wollen wir diese wichtige Wahrscheinlichkeitsverteilung etwas genauer vorstellen. Dafür werden wir zunächst die Grundlagen und Motivation für Wahrscheinlichkeitsverteilungen im Allgemeinen darstellen. Im Anschluss wird dann die Normalverteilung (Gauss-Verteilung) im Speziellen besprochen und deren Wichtigkeit erläutert. Dabei gehen wir auch auf den zentralen Grenzwert näher ein und zeigen ein zentraler Grenzwertsatz Beispiel.
Was ist eine Wahrscheinlichkeitsverteilung?
Wann immer wir Dinge modellieren wollen, bei denen der Zufall im Spiel ist, sind Wahrscheinlichkeitsverteilungen ein unersetzliches Tool in der statistischen Werkzeugkiste.
Eine Wahrscheinlichkeitsverteilung (auch einfach „Verteilung“ genannt) ist eine Funktion, die dabei hilft, die Wahrscheinlichkeit für alle möglichen Werte zu berechnen, die eine zufällige Variable annehmen kann. Zum Beispiel lässt sich der Wurf eines fairen Würfels mit einer Wahrscheinlichkeitsverteilung darstellen. Dabei wird jeder der Augenwerte 1-6 eine Wahrscheinlichkeit von 1/6 zugeteilt. Diese Verteilung wird als Gleichverteilung bezeichnet und ist eine der einfachsten Verteilungen.
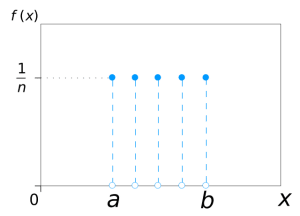
Normalverteilung einfach erklärt
So weit haben wir aber eine entscheidende Frage noch nicht geklärt: Was bedeutet normalverteilt? Bei vielen komplexeren Zusammenhängen ist es realistischer, eine sogenannte Normalverteilung anzunehmen. Ein gutes Normalverteilung-Beispiel hierfür stellt ein Dartspieler dar, der versucht, das “Bull’s-Eye” zu treffen. Die zufällige horizontale Abweichung in cm lässt sich hierbei akkurat durch eine Normalverteilung wie darstellen:
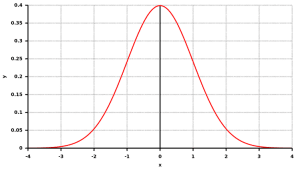
Wir sehen hier eine typische (gausssche) Glockenkurve. Die Glockenkurve (und damit die Gauss-Verteilung) wird charakterisiert durch zwei Parameter – den Mittelwert µ und die Standardabweichung σ (diese gibt die „Streuung“ an). Je schlechter der Dartspieler ist, desto grösser wird die Standardabweichung sein.
Eine ausführlichere Einführung in verbreitete Verteilungen findet sich hier.
Wahrscheinlichkeitsverteilungen sind nützlich, wenn man für ein Zufallsereignis wissen muss, welche Ergebnisse am wahrscheinlichsten sind. Im Falle des Dartspielers wäre das eine Abweichung von 0 cm, also das Treffen des Bull’s-Eyes. Wahrscheinlichkeitsverteilungen sind auch wichtig um festzustellen, in welchem Wertebereich sich potenzielle Ergebnisse befinden (etwa im Bereich +-4 cm) und wie wahrscheinlich unterschiedliche Ergebnisse sind (abnehmende Wahrscheinlichkeit mit zunehmender Entfernung vom Bull’s-Eye).
Nun haben wir bereits einiges an Vorwissen zu der Frage “Was bedeutet normalverteilt?” behandelt. Kommen wir nun also zu den Gründen, die die Gauss-Verteilung so wichtig machen.
Warum die Normalverteilung die wichtigste Verteilung ist – Top 3
1) Zentraler Grenzwertsatz
Der Hauptgrund für die zentrale Stellung der Normalverteilung in der angewandten Statistik und Mathematik ist der zentrale Grenzwertsatz. In einfachen Worten sagt er aus, dass die Aggregation mehrerer unabhängiger Zufallsvariablen egal welcher Verteilung zu einer Normalverteilung tendiert. Unter „Aggregation“ versteht man hier vor Allem Summen- oder Durchschnittsbildung. Am besten lässt der zentrale Grenzwertsatz sich an Beispielen verstehen. Eine ausführliche theoretische Abhandlung findet sich beispielsweise hier.
Zentraler Grenzwertsatz Beispiel #1: Telefonumfrage
Angenommen, Sie möchten herausfinden, wie viele Menschen in Deutschland Schokolade mögen. Daher rufen Sie eine zufällige Person an und fragen “Mögen Sie Schokolade?”. Falls diese Person mit “Ja” antwortet, ist die beste Schätzung für die Menschen, die Schokolade mögen (ohne anderweitige Information) 100%. Falls die Person mit “Nein” antwortet, ist die beste Schätzung entsprechend 0%. Anschliessend rufen Sie eine zweite Person an, dann eine dritte, eine vierte, usw. Nachdem Sie 500 Personen angerufen und nach Ihrer Präferenz befragt haben, beenden Sie Ihre Umfrage und kommen zum Schluss “Laut meiner Umfrage mögen 37% der Leute Schokolade”.
Nehmen wir Sie starten eine weitere Umfrage mit 500 Personen. Aufgrund des Zufalls erwarten Sie ein anderes Ergebnis – beispielsweise 39%. Nun wiederholen Sie die Umfrage viele Male und befragen jedes mal 500 Leute.
Nun wird es interessant: Wenn Sie a) eine grosse Zahl an Leuten anrufen b) die Antworten dieser Leute unabhängig sind und c) Sie eine grosse Anzahl an Umfragen durchführen sowie d) einige technische Bedingungen des zentralen Grenzwertsatzes erfüllt sind, dann wird der zentrale Grenzwertsatz dafür sorgen, dass die Umfragewerte sich in einer Glockenkurve anordnen, also normalverteilt sind.
Wir sehen: Die Aggregation (in diesem Fall: Mittelwertbildung) einer grossen Anzahl von unabhängigen Zufallsvariablen (einzelnen Anrufen) folgt asymptotisch (wir führen die Umfrage viele Male durch) einer stabilen Verteilung – der Normalverteilung.
Zentraler Grenzwertsatz Beispiel 2: Würfeln
Angenommen, Sie würfeln 2 6-seitige (faire) Würfel. Die Würfe sind alle unabhängig, da keine der Würfe einen der anderen Würfe beeinflusst. Für einen einzelnen Würfel ist die Chance für eine 1, 2, 3, 4, 5 oder 6 identisch (diskrete Gleichverteilung).
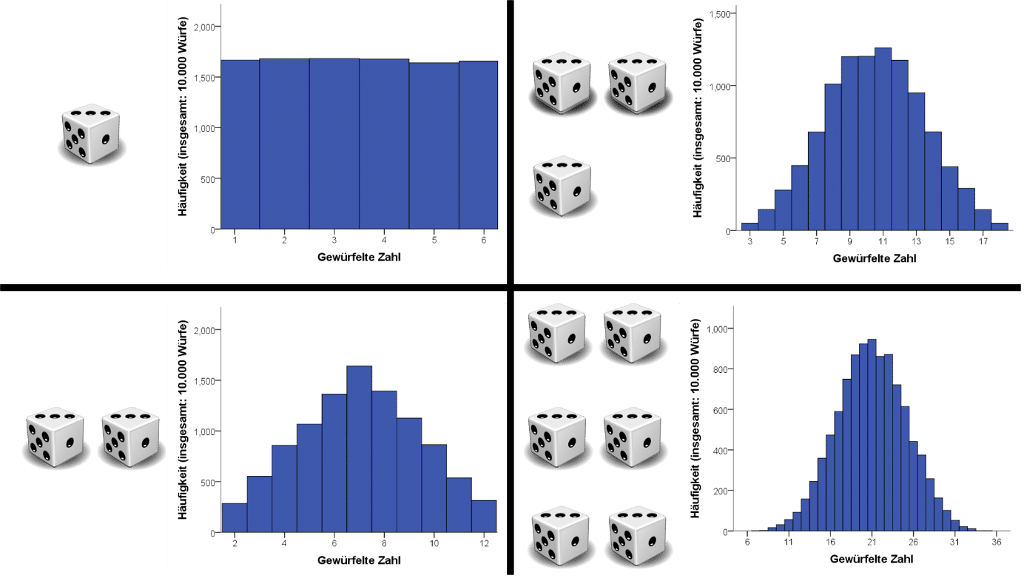
Wenn wir nun die Augenzahlen von zwei Würfeln addieren, haben wir eine Wahrscheinlichkeit von 1/36, dass die Summe 2 ergibt. Weiterhin haben wir eine Wahrscheinlichkeit von 2/36, eine 3 zu erhalten und eine Wahrscheinlichkeit von 3/36, eine 4 zu erhalten. Die Wahrscheinlichkeiten nehmen zu bis wir eine Wahrscheinlichkeit von 6/36, eine 7 zu erhalten. Dann nimmt die Wahrscheinlichkeit wieder ab, bis die Wahrscheinlichkeit, eine 12 zu erhalten, wieder bei 1/36 liegt. Das liegt daran, dass die Werte in der Mitte, wie z.B. die 7, erreicht werden können, indem man die Augenzahlen 1 + 6, 6 + 1, 2 + 5, 5 + 2, 3 + 4 oder 4 + 3 erhält, während die Grenzfälle wie die 2 ein einziges sehr spezifisches Ergebnis (1 + 1) erfordern.
Zentraler Grenzwertsatz für viele Würfel
Wenn Sie nun die Anzahl der gewürfelten Würfel weiter erhöhen (auf n), werden die Grenzfälle immer unwahrscheinlicher (z. B. dass jeder von 10 Würfeln eine 1 zeigt). Dies liegt daran, dass sie immer wieder sehr spezifische Ergebnisse erfordern. Die Ergebnisse in der Mitte werden dagegen wahrscheinlicher. Je mehr Würfel Sie hinzufügen, desto mehr wird es letztendlich wie eine Glockenkurve aussehen.
Nun werfen wir diese n Würfel nicht nur einmal, sondern viele Male. Dann sehen wir erneut, dass die Aggregation (in diesem Fall: Mittelwertbildung) einer grossen Anzahl von unabhängigen Zufallsvariablen (einzelnen Würfen von n Würfeln) asymptotisch (wir führen die Umfrage viele Male durch) einer stabilen Verteilung folgt – der Normalverteilung. Die Abbildung oben verdeutlicht dies in anschaulicher Weise.
2) Vielfältige Anwendbarkeit der Normalverteilung
Die Normalverteilung tritt in vielen zentralen Anwendungen und Problemen auf.
Beispiele für die Anwendungen der Normalverteilung sind biologische Grössen (Körpergrösse, Länge von Haaren, Armen, etc., Blutdruck usw.), Finanzmarktgrössen (stündliche / tägliche Preisänderungen von Aktien), Messfehler in der Physik, natürliche Grössen (Regenmenge, Sonnenscheindauer innerhalb eines Jahres) oder in der Produktion (Qualitätssicherung, Analyse von Produktionskapazitäten).
Ein weiterer Grund für die Wichtigkeit der Normalverteilung ist deren vielfältige Anwendbarkeit im Kontext von statistischen Tests. Viele Tests basieren auf der zentralen Annahme, dass beteiligte Variablen normalverteilt sind. Diese Tests können sonst nicht durchgeführt werden.
Beispielsweise müssen bei Regressionsanalysen und Varianzanalysen die Residuen normalverteilt sein, sodass der Schätzer unverzerrte Ergebnisse liefert. Es existiert eine Fülle von Tests auf Normalverteilung (siehe Wikipedia oder unseren Blogartikel mit einem SPSS-Beispiel). Auch im Falle der Varianzanalyse oder t-Tests sind Normalverteilungen zentral. Sollten Sie professionelle Hilfe bei Ihrer statistischen Arbeit benötigen, können wir Sie gerne mit einer Statistik Beratung unterstützen.
Auch vereinfacht die Normalverteilung die Berechnung verschiedenster statistischer Grössen wie Mittelwerte, Varianzen sowie Korrelationen zwischen Variablen. Daher ist die Normalverteilung auch in Fällen, wo die Daten vielleicht nur annähernd normalverteilt sind, eine valide Option, um ein erstes Verständnis für die Daten zu erhalten.
3) Die 68-95-99.7 Regel
Die 68-95-99.7 Regel ist eine empirische Regel der angewandten Statistik, die einen anschaulichen Zusammenhang zwischen Mittelwert und Standardabweichung eines normalverteilten Zufallsereignisses ermöglicht. Sie gibt an, wie viel Prozent der Messwerte innerhalb einer, zwei bzw. drei Standardabweichungen σ vom Mittelwert μ entfernt sind.
Zum Beispiel zeigt Abbildung 4 die Verteilung der Körpergrösse von Männern. Der Mittelwert μ beträgt 170 cm, die Standardabweichung σ beträgt 10 cm. Die 68-95-99.7 Regel besagt nun, dass:
- 68 % aller Männer zwischen 160 cm und 180 cm gross sind.
- 95 % aller Männer zwischen 150 cm und 190 cm gross sind.
- 99,7 % aller Männer zwischen 140 cm und 200 cm gross sind.
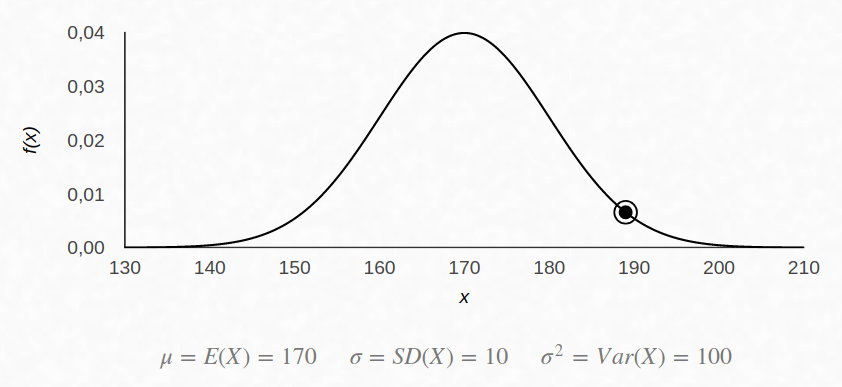
Weiter oben haben wir gesehen, dass die Normalverteilung in vielfältigen Einsatzgebieten auftritt. Mithilfe der 68-95-99.7-Regel lassen sich einfache Aussagen über die beteiligten Variablen treffen, was die Interpretierbarkeit von Daten erheblich erleichtern kann.
Die Normalverteilung: Eine vielfältig einsetzbare Wahrscheinlichkeitsverteilung
In diesem Artikel haben wir zunächst die Frage “Was bedeutet normalverteilt?” geklärt. Daraufhin sind wir auf die Bedeutung der Normalverteilung eingegangen. Die Gausssche Normalverteilung ist die wichtigste Wahrscheinlichkeitsverteilung. Der Hauptgrund hierfür ist der zentrale Grenzwertsatz, der aussagt, dass unter bestimmten Voraussetzungen jede beliebige Verteilung asymptotisch zu einer Normalverteilung wird. Die Normalverteilung ist auch anderweitig vielfältig einsetzbar, um vielfältige Zufallsgrössen und -prozesse akkurat zu modellieren. Auch in der statistischen Modellierung und in vielen (vor allem parametrischen) Hypothesentests ist die Normalverteilung zentraler Bestandteil. Die 68-95-99.7-Regel ist eine Faustregel, die Sie sich zunutze machen können, um in Ihren Analysen schnelle Aussagen über vielfältige normalverteilte Variablen zu treffen. Falls Sie Fragen zu einem dieser Themen haben, stehen unsere Experten für eine Statistik Beratung gerne zur Seite.
Weiterführende Links
Buchkapitel zur Normalverteilung