Fehlerbalken und Konfidenzintervalle in R visualisieren

Eine fundierte Datenanalyse geht über Mittelwerte und Häufigkeiten hinaus. Ebenso wichtig ist es jedoch, die Variabilität von Daten sichtbar zu machen. Denn egal ob es um Cholesterinspiegel, Patientenzufriedenheit oder die Lebenserwartung geht: Ohne zusätzliche Informationen über Streuung und Unsicherheit bleibt das Gesamtbild unvollständig.

Ein Beispiel: Zwei Länder haben im selben Jahr eine ähnliche durchschnittliche Lebenserwartung. Betrachtet man nur den Mittelwert, scheint die Situation vergleichbar. Doch die Streuung innerhalb der Länder unterscheidet sich deutlich. Während in Land A die Werte eng beieinanderliegen, zeigen sich in Land B grosse Unterschiede. Erst durch eine grafische Darstellung mit Fehlerbalken – typischerweise als 95%-Konfidenzintervall – wird sichtbar, wie heterogen die Situation tatsächlich ist. Darüber hinaus liefert diese Visualisierung wertvolle Hinweise auf mögliche Einflussfaktoren.

Visualisierung schafft hier Mehrwert: Komplexe Konzepte wie Unsicherheit und Präzision werden unmittelbar verständlich. Mit der Statistiksoftware R und dem Paket ggplot2 lassen sich Konfidenzintervalle mit wenigen Zeilen Code berechnen und grafisch darstellen.

Fehlerbalken – Variabilität auf einen Blick

Fehlerbalken sind ein grafisches Hilfsmittel, um Unsicherheit darzustellen. Sie werden als Linien ober- und unterhalb eines Werts (meist des Mittelwerts) gezeichnet. Entscheidend ist, welches Mass zugrunde liegt:

• Standardabweichung (SD): zeigt die Streuung der Einzelwerte um den Mittelwert.
• Standardfehler (SE): zeigt die Unsicherheit der Mittelwertschätzung.
• Konfidenzintervall (Confidence Interval [CI] / Vertrauensintervall): zeigt den Bereich, in dem der wahre Mittelwert mit einer bestimmten Wahrscheinlichkeit (z. B. 95 %) liegt.

Beispiel Lebenserwartung: Beide Länder weisen eine durchschnittliche Lebenserwartung von 75 Jahren auf. Während die Werte in Land A homogen verteilt sind und kurze Fehlerbalken ergeben, zeigt Land B eine starke Streuung mit langen Fehlerbalken. Auch ohne komplexe Statistik wird dadurch sichtbar, dass die Datenlage in Land B uneinheitlicher ist.

Konfidenzintervalle – Präzision mit statistischer Grundlage

Fehlerbalken sind die Darstellung, das Konfidenzintervall das zugrunde liegende Mass.

Ein Konfidenzintervall gibt den Bereich an, in dem der wahre Mittelwert einer Grundgesamtheit mit hoher Wahrscheinlichkeit liegt. Bei einem 95%-Konfidenzintervall gilt: Würde man die Studie oft wiederholen, würden etwa 95 von 100 Intervallen den wahren Wert einschliessen. Notiert wird es als [L; U] mit:

Untergrenze (L): kleinster plausibler Wert für den wahren Mittelwert
Obergrenze (U): grösster plausibler Wert für den wahren Mittelwert

In der Praxis haben sich Konfidenzintervalle als Fehlerbalken aus mehreren Gründen durchgesetzt:

• Eindeutige Interpretation: Ein 95 %-Konfidenzintervall erlaubt die klare Aussage: Mit hoher Wahrscheinlichkeit liegt der wahre Mittelwert in diesem Bereich.
• Vergleichbarkeit: Konfidenzintervalle sind standardisiert und in der wissenschaftlichen Publikation etabliert. Das erleichtert den Vergleich von Studien oder Gruppenergebnissen.
• Robustheit: Während der Standardfehler lediglich die Präzision des Mittelwerts anzeigt, zeigt das Konfidenzintervall hingegen ausdrücklich, wie gross die Unsicherheit tatsächlich ist.

Beispiel Lebenserwartung: Land A hat konsistente Daten, z. B. 95% CI [74; 76]. Land B ist heterogener, z. B. 95% CI [70; 80]. Konfidenzintervalle verdeutlichen so die Aussagekraft der deskriptiven Analyse.

Konfidenzintervall (95 %) berechnen: Formel

Ein 95%-Konfidenzintervall um den Mittelwert wird mit folgender Formel berechnet:

95% CI = x̄ ± 1.96 × SE

• x̄ = Mittelwert der Stichprobe
• SE = Standardfehler = SD / √n
• 1.96 = Kritischer Wert der Normalverteilung für 95 %

Damit ergibt sich:

Untergrenze (L) = Mittelwert – 1.96 × SE
Obergrenze (U) = Mittelwert + 1.96 × SE

Der Standardfehler hängt also unmittelbar von der Standardabweichung ab. Das bedeutet: Je grösser die Streuung in den Daten ist, desto grösser wird auch das resultierende Konfidenzintervall.

Konfidenzintervalle berechnen und visualisieren in R

Die Statistiksoftware R bietet leistungsstarke Werkzeuge, um Variabilität anschaulich darzustellen. Mit Paketen wie ggplot2 lassen sich Fehlerbalken unkompliziert erzeugen. Je nach Fragestellung können diese Standardabweichung, Standardfehler oder das Konfidenzintervall abbilden.

Wir zeigen zwei Beispiele mit dem gapminder-Datensatz mit Informationen zur Lebenserwartung.

Umsetzung in R mit ggplot2: Code und Abbildung

Vorbereitung

Zunächst werden der Datensatz sowie die erforderlichen Pakete geladen.

# Packages installieren (falls erforderlich) und laden

install.packages(c("gapminder", "dplyr", "ggplot2"))
library(gapminder)
library(dplyr)
library(ggplot2)

Variablen kurz erklärt

Der Datensatz beinhaltet 6 Variablen:

• country: Name des Landes
• continent: Kontinent
• year: Jahr der Messung
• lifeExp: Lebenserwartung in Jahren
• pop: Bevölkerungszahl
• gdpPercap: Bruttoinlandsprodukt pro Kopf in US-Dollar

Hinweis: Für 2007 enthält der Datensatz die jüngste Messung je Land. Insgesamt handelt es sich um Paneldaten mit rund 1700 Zeilen.

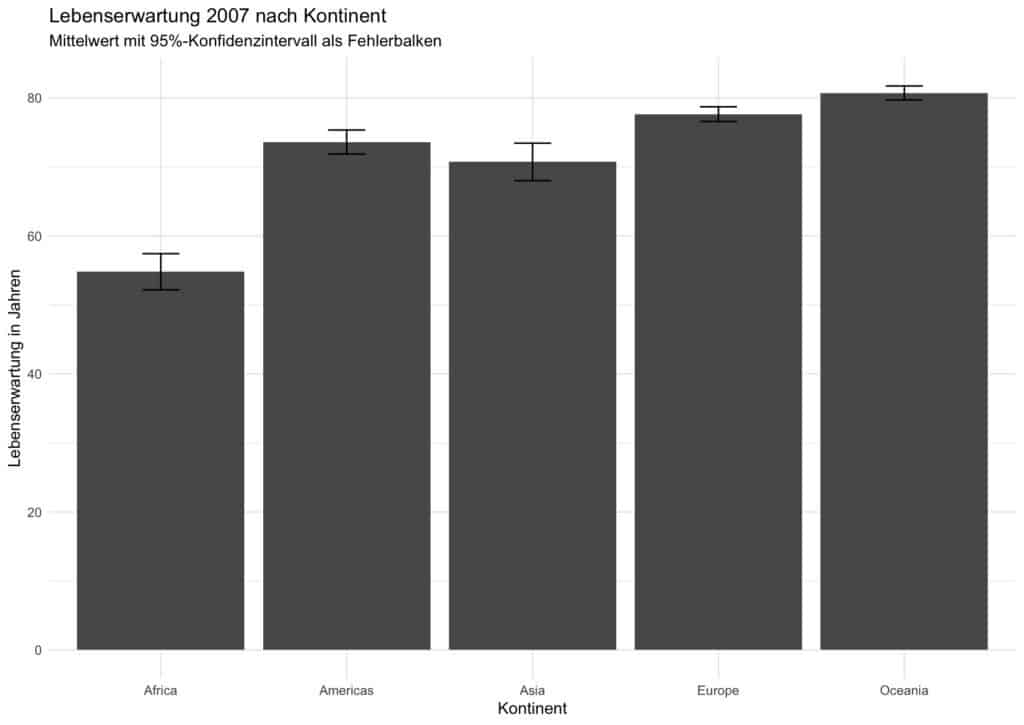
Beispiel 1: Lebenserwartung nach Kontinent im Jahr 2007 mit 95-Prozent-Konfidenzintervall

Im ersten Beispiel konzentrieren wir uns auf das Jahr 2007 und vergleichen die durchschnittliche Lebenserwartung zwischen den Kontinenten. Im ersten Schritt berechnen wir je Kontinent Mittelwert, Standardfehler und 95-Prozent-Konfidenzintervall; im zweiten Schritt visualisieren wir die Ergebnisse als Balkendiagramm mit Fehlerbalken.

# Daten filtern (nur Jahr 2007, pro Kontinent zusammen)
# Mittelwerte, Standardfehler und Konfidenzintervalle berechnen

df_2007 <- gapminder %>%
  filter(year == 2007) %>%
  group_by(continent) %>%
  summarise(
    n = n(),                                    # Anzahl Länder je Kontinent
    mean_life = mean(lifeExp, na.rm = TRUE),    # Mittelwert Lebenserwartung
    se = sd(lifeExp, na.rm = TRUE) / sqrt(n),   # Standardfehler = SD / √n
    ci_lower = mean_life - 1.96 * se,           # Untere Grenze 95%-KI
    ci_upper = mean_life + 1.96 * se,           # Obere Grenze 95%-KI
    .groups = "drop" # Gruppierung aufheben
)


# Visualisierung Balkendiagramm mit Konfidenzintervallen als Fehlerbalken
# Titel und Achsenbeschriftung festlegen

ggplot(df_2007, aes(x = continent, y = mean_life)) +
  geom_col() +                                  # Balken = Mittelwert
  geom_errorbar(aes(ymin = ci_lower, ymax = ci_upper),
                width = 0.2, color = "black") + # Fehlerbalken = 95%-KI
  labs(
    title = "Lebenserwartung 2007 nach Kontinent",
    subtitle = "Mittelwert mit 95%-Konfidenzintervall als Fehlerbalken",
    x = "Kontinent",
    y = "Lebenserwartung in Jahren"
  ) +
  theme_minimal()

Die Balken zeigen die geschätzten Mittelwerte pro Kontinent im Jahr 2007, die Fehlerbalken die jeweiligen 95-Prozent-Konfidenzintervalle. Engere Intervalle deuten auf eine präzisere Schätzung des Kontinentalmittelwerts hin. Ob sich die Kontinente tatsächlich unterscheiden, lässt sich aus einer blossen Überlappung der Konfidenzintervalle nicht eindeutig ableiten. Um Unterschiede zuverlässig nachzuweisen, müssen zusätzlich geeignete statistische Tests wie beispielsweise ein t-Test oder eine ANOVA durchgeführt werden.

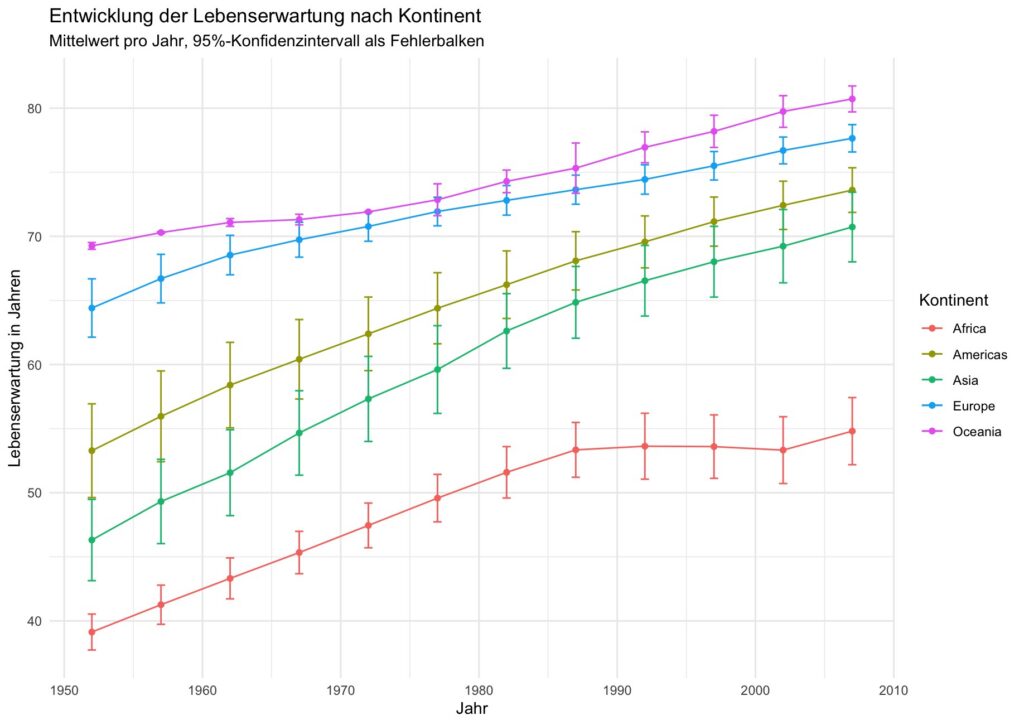
Beispiel 2: Entwicklung der Lebenserwartung über die Zeit mit 95%-Konfidenzintervallen

Im zweiten Beispiel betrachten wir die Entwicklung der Lebenserwartung über die Zeit. Wir fassen die Daten erneut pro Kontinent zusammen, diesmal jedoch auch für jedes Jahr im Datensatz. Anschliessend visualisieren wir die Zeitreihe der Mittelwerte mit Fehlerbalken für die 95%-Konfidenzintervalle.

# Zeitreihe pro Kontinent zusammenfassen

df_time <- gapminder %>%
  group_by(continent, year) %>%
  summarise(
    n = n(),
    mean_life = mean(lifeExp, na.rm = TRUE),
    se = sd(lifeExp, na.rm = TRUE) / sqrt(n),
    ci_lower = mean_life - 1.96 * se,  
    ci_upper = mean_life + 1.96 * se,  
    .groups = "drop"                           
  )


# Linienplot mit Konfidenzintervallen als Fehlerbalken

ggplot(df_time, aes(x = year, y = mean_life, color = continent)) +
  geom_line() +                                # Linien = Entwicklung über die Zeit
  geom_point() +                               # Punkte = Mittelwerte
  geom_errorbar(aes(ymin = ci_lower, ymax = ci_upper),
                width = 0.6) +
  labs(
    title = "Entwicklung der Lebenserwartung nach Kontinent",
    subtitle = "Mittelwert pro Jahr, 95%-Konfidenzintervall als Fehlerbalken",
    x = "Jahr",
    y = "Lebenserwartung in Jahren",
    color = "Kontinent"
  ) +
  theme_minimal()

Die Fehlerbalken zeigen 95-Prozent-Konfidenzintervalle der Kontinentalmittelwerte pro Jahr. Ihre Breite wird von zwei Faktoren bestimmt, der Streuung der Länderwerte und der Anzahl der Länder. Enge Intervalle können auch bei kleiner Länderzahl auftreten, wenn die Länder ähnlich sind, breite Intervalle deuten häufig auf grössere Heterogenität hin.

Diese beiden Beispiele verdeutlichen, wie einfach sich Konfidenzintervalle in R als Fehlerbalken visualisieren lassen. Mit wenigen Zeilen Code kann man die Unsicherheit statistischer Schätzungen anschaulich darstellen und so Analysen transparenter und interpretierbarer machen. Besonders im medizinischen und gesundheitlichen Kontext trägt dies dazu bei, Ergebnisse nicht zu überinterpretieren und die Aussagekraft korrekt einzuschätzen.

Interpretation und typische Stolperfallen der Konfidenzintervalle

Die Visualisierung von Konfidenzintervallen als Fehlerbalken ist ein geeignetes Werkzeug, um Unsicherheit und Variabilität verständlich zu machen. Dennoch gibt es einige Punkte, die bei der Interpretation beachtet werden sollten:

• Man sollte immer klar angeben, was die Fehlerbalken darstellen. Sind es Standardabweichungen, Standardfehler oder 95 %-Konfidenzintervalle? Ohne diese Information ist die Grafik leicht missverständlich.
• Überlappende Konfidenzintervalle sind kein Beweis für „keinen Unterschied“. Sie deuten lediglich darauf hin, dass sich die Intervalle überschneiden. Für eine formale Prüfung, ob ein Unterschied statistisch signifikant ist, braucht es geeignete Tests.
• Ein Konfidenzintervall bezieht sich auf den Mittelwert, nicht auf Einzelfälle. Es sagt nichts darüber aus, in welchem Bereich sich die individuellen Werte bewegen, sondern beschreibt die Unsicherheit der Schätzung des Mittelwerts.
• Berücksichtige bei der Interpretation die Stichprobengrösse. Kleine n führen zu breiteren Konfidenzintervallen. Das ist kein Fehler, sondern ein Hinweis darauf, dass die Datenlage weniger stabil ist.
• Halte die Skalierung und Achsendarstellung stets einheitlich. Unterschiedliche Skalierungen können die optische Wirkung verfälschen, sodass Balken schnell „dramatisch“ erscheinen, obwohl die tatsächliche Unsicherheit gering ist.

Fazit

Fehlerbalken machen die Variabilität sichtbar und Konfidenzintervalle liefern dafür die notwendige statistische Grundlage. In R lassen sich beide einfach berechnen und darstellen. Wer die Berechnung des Konfidenzintervalls klar dokumentiert und die Stichprobengrösse angibt, sorgt für Transparenz und vermeidet Fehlinterpretationen.