Die Kurtosis (oder Wölbung) ist gemeinsam mit der Schiefe ein zentrales Konzept, um die Verteilung einer Wahrscheinlichkeitsfunktion zu beschreiben. Die Kurtosis gibt an, wie steil oder flach der Verlauf einer Kurve ist, die Schiefe gibt an, ob der Verlauf symmetrisch ist oder die Kurve auf einer Seite steiler verläuft als auf der anderen.
Sie benötigen Unterstützung bei der Berechnung und Interpretation der Verteilung von Wahrscheinlichkeitsfunktionen und der Frage nach Normalverteilung ja/nein? – Dann wenden sie sich hierzu an uns für eine professionelle Statistik Beratung!
Der folgende Artikel stellt das Thema vor und beantwortet folgende Fragen:
- Wie wird die Kurtosis (oder Wölbung) berechnet?
- Was ist der Unterschied zwischen Kurtosis und Exzess?
- Was ist die Schiefe und was bedeuten rechtsschied und linksschief?
Kurtosis Interpretation: So wird sie berechnet
Wölbung und Kurtosis sind zwei unterschiedliche Begriffe für den gleichen Sachverhalt und werden häufig mit mit dem Symbol β2 oder α4 abgekürzt. Die klassische Wölbung beschreibt, ob eine Kurve eher flachgipflig oder steilgipflig verläuft.
Je kleiner der Wert, desto flacher ist die Kurve, je höher, desto steiler. Negative Werte sind dabei nicht möglich. Eine Normalverteilung hat eine Kurtosis von 3.
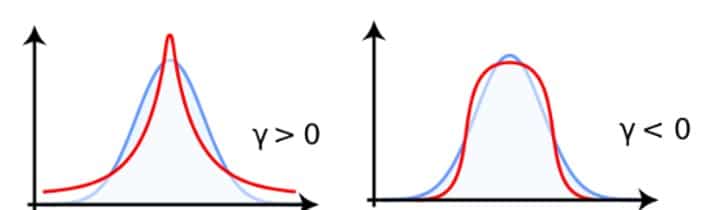
Berechnet wird der Wert ähnlich wie die Varianz. Von jedem Wert wird zunächst die Differenz zum arithmetischen Mittel berechnet. Diese Differenz wird allerdings nicht quadriert – wie bei der Berechnung von Varianz und Normalverteilung – sondern zunächst durch die Standardabweichung geteilt und dann hoch 4 gerechnet.
Diese Berechnung wird für alle Werte durchgeführt. Das arithmetische Mittel daraus ergibt die (verzerrte) Wölbung:
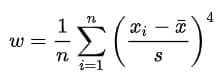
Unterschied Kurtosis und Exzess
Wölbung und Kurtosis sind also wie beschrieben zwei synonyme Begriffe. Oftmals wird in diesem Zusammenhang auch der Begriff Exzess (gekennzeichnet mit dem griechischen Symbol γ) fälschlicherweiser als Synonym verwendet.
Tatsächlich beschreibt der Exzess die Differenz der Wölbung zur Normalverteilung beschrieben. Um diesen Wert leichter interpretierbar zu machen, wird die Wölbung meist in Relation zur Normalverteilung betrachtet. Diese Kennzahl wird als Exzess bezeichnet.
Weil die Wölbung bei einer normalverteilten Kurve 3 ist, wird von der berechneten Wölbung der Wert 3 abgezogen. Das daraus resultierende Ergebnis ist der Exzess.
Im Gegenzug zur klassischen Wölbung sind hier auch Werte kleiner Null möglich. Sie stehen für einen Verlauf, der flacher als der bei Normalverteilung ist. Bei einem Exzess grösser Null ist der Verlauf steiler.
| Wölbung (β2 oder α4) | Exzess (γ) | Beschreibung |
| < 3 | < 0 | flachgipflig |
| = 3 | = 0 | symmetrisch; entspricht Normalverteilung |
| > 3 | > 0 | steilgipflig |
Exzess oder Kurtosis verwenden?
Der Exzess ist das gebräuchlichere Mass, teilweise wird unter dem Namen Kurtosis oder Wölbung der Exzess angegeben. So verbirgt sich zum Beispiel in Excel unter der Formel =KURT() die Berechnung für den Exzess.
Auch in Texten zur Kurtosis liest man oft den Hinweis, Werte unter Null würden für einen flachgipfligen Verlauf stehen, obwohl sich diese Aussage streng genommen auf den Exzess bezieht.
Um Missverständnissen vorzubeugen, ist es ratsam, den Exzess anstelle der klassischen Wölbung auszuweisen, da die Bezeichnung eindeutiger und leichter zu interpretieren ist.
Schiefe: Linksschief oder rechtsschief
Auch das Konzept der Schiefe lässt sich am einfachsten verstehen, wenn wir die Normalverteilung als Ausgangspunkt nehmen. Die Kurve ist symmetrisch, sie verläuft auf beiden Seiten des Mittelwertes genau spiegelbildlich.
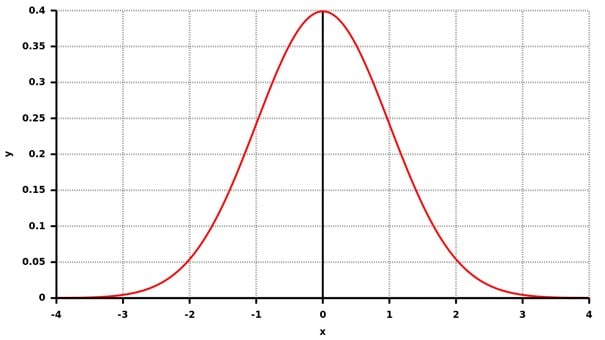
Die Normalverteilung mit symmetrischem Verlauf zu beiden Seiten ist allerdings eher ein Sonderfall. Oft ist der Verlauf nicht symmetrisch, sondern die Kurve ist zur einen oder anderen Seite geneigt.
Einkommen sind beispielsweise überwiegend rechtsschief verteilt. Es gibt wenige Personen mit niedrigem Einkommen, in der Mitte steigt die Dichte stark an (Median) und nimmt dann wieder ab. Im oberen Einkommensbereich, d.h. im oberen Quantil (bzw. Perzentil) liegen die Werte weit auseinander.
Hier finden sich die – verhältnismässig – wenigen Multimillionäre, die Abstände sind folglich besonders gross. Aus diesem Grund verläuft die Kurve im oberen Bereich sehr flach und zeigt eine rechtsschiefe Verteilung.
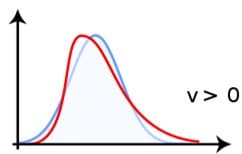
Linkssteil oder rechtsschief?
Anstatt des Begriffs rechtsschief lässt sich auch die Bezeichnung linkssteil verwenden. Beide Begriffe meinen genau dasselbe, sind also Synonyme. Die Bezeichnung linkssteil ist allerdings anschaulicher.
Umgekehrt gibt es natürlich auch linksschiefe (rechtssteile) Verteilungen. Ein Beispiel dafür ist die Besiedlung von verschiedenen einander ähnlichen Habitaten mit Tieren. Diese bieten einer bestimmten Anzahl von Tieren eine Lebensgrundlage.
Die Zahl der Lebewesen dort wächst solange an, bis sie die Nähe dieser Obergrenze erreicht hat (und daher liegt deren Zahl in den meisten Gegenden nahe dieser Obergrenze). Nach unten gibt es dagegen deutliche Abweichungen, etwa wenn eine Krankheit oder ein Naturereignis (Feuer, etc.) die Zahl der Tiere reduziert.
So wird die Schiefe berechnet
Die Berechnung der Schiefe ähnelt jener der Kurtosis und ist ebenfalls mit der Varianz verwandt. Wie bei der Wölbung wird für jeden Wert die Abweichung zum arithmetischen Mittel berechnet und diese Differenz dann durch die Standardabweichung geteilt.
Dieses Ergebnis wird aber nicht mit 4, sondern mit 3 potenziert. Schliesslich wird, analog zur Varianz und zur Kurtosis, aus all diesen Werten das arithmetische Mittel berechnet.
Kurzer Exkus zur Verdeutlichung: Anders formuliert ist die Kurtosis das vierte und die Schiefe das dritte zentrale Moment, jeweils normiert durch die Standardabweichung. Die Varianz ist folglich das zweite zentrale Moment, sie wird nicht normiert, und schliesslich die Standardabweichung als erstes Moment, die sich aus der (Quadratwurzel der) Varianz errechnet.
Schiefe und Kurtosis in Excel berechnen
Sowohl die Kurtosis als auch die Schiefe lassen sich mit den üblichen Statistikprogrammen wie R und SPSS, aber auch mit Tabellenkalkulationsprogrammen wie Excel oder LibreOffice berechnen.
Excel und Statistikprogramme wie SPSS verwenden zur Berechnung der Kurtosis oder des Exzesses oft eine etwas komplexere Formel, die sogenannte unverzerrte Wölbung. Die Unterschiede zur verzerrten Wölbung sind aber gering.
Für aussagekräftige Analysen mit Excel lautet hier wie erwähnt die Formel für die Berechnung der Kurtosis =KURT(), wobei in Klammern der Datenbereich eingefügt wird. Allerdings gibt Excel hier den Exzess aus. Um tatsächlich die Wölbung zu erhalten, müssen wir zum Ergebnis den Wert 3 addieren.
Für die Berechnung der Schiefe kennt Excel zwei Befehle (und LibreOffice Calc oder OpenOffice folgen dieser Aufteilung), konkret:
Mit =SCHIEFE() lässt sich die Schiefe für eine Stichprobe berechnen, mit =SCHIEFE.P() für die Grundgesamtheit.
Schiefe und Kurtosis in SPSS und R
Mit der SPSS-Software lassen sich Kurtosis und Schiefe einfach per Mausklick berechnen. Dazu muss im Menüpunkt Analysieren der Unterpunkt Deskriptive Statistik aufgerufen werden. Hier finden sich im Rahmen der Analyse von Häufigkeiten beide Werte. Wer mit englischsprachigen Versionen arbeitet, wählt für die Schiefe den Begriff skewness.
Auch beim Arbeiten mit R lautet der Befehl für die Schiefe in den meisten Paketen skewness, etwa im Paket moments. Der Befehl zur Berechnung der Kurtosis lautet in diesem Paket entsprechend kurtosis.
Im Gegensatz zu Excel berechnet R hier tatsächlich die Wölbung und nicht den Exzess, der Wert von 3 steht also für eine Normalverteilung, Werte von unter 3 für eine flachgipflige, Werte über 3 für eine steilgipflige Verteilung.
Wichtig ist, dass bei R die Gross- und Kleinschreibung der Befehle eine Rolle spielt, im Paket moments werden beide Befehle klein geschrieben. In Klammern dahinter wird der Datenbereich angegeben.
Fazit
Kurtosis und Schiefe sind relevante und sehr nützliche Kennzahlen, um Verteilungen zu beschreiben. Anhand dieser beiden Werte wird auch schnell und offenkundig sichtbar, ob die Daten (annähernd) normalverteilt sind.
Eine Schiefe nahe 0 und eine Kurtosis von etwa 3 sprechen für eine Normalverteilung. Statt der Kurtosis wird oft der Exzess betrachtet. Dabei wird von der Kurtosis der Wert 3 abgezogen, sodass eine Normalverteilung den Wert 0 hat. Werte < 0 sprechen für einen im Vergleich zur Normalverteilung flacheren, Werte > 0 für einen steileren Verlauf.
Bei Unklarheiten und Unterstützungsfragen freuen wir uns auf Ihre schriftliche Kontaktaufnahme über unser Anfrageformular. Gerne unterstützen wir Sie und erstellen Ihnen unverbindlich ein individuelles Angebot!