Die Normalverteilung ist eine der bekanntesten Verteilungen in der Statistik. Viele Verfahren beruhen massgeblich auf den Eigenschaften normalverteilter Daten (z.B. t-Test, lineare Regression). Aber gerade die Frage nach der Verteilung der Daten stellt viele Anwender vor eine grosse Herausforderung. Mit welchen Verfahren soll der Test auf Normalverteilung durchgeführt werden? Welches Verfahren ist richtig? In diesem Artikel stellen wir Ihnen die wichtigsten explorativen Verfahren vor und stellen die Verfahren in einem R Shiny Dashboard übersichtlich zur Verfügung.
Gerne unterstützen wir Sie bei der Überprüfung und der Auswahl geeigneter Verfahren, auch bei einer Verletzung der Normalverteilungsannahme. Genauso können wir auch für Ihr Projekt ein attratktives Shiny Dashboard erstellen.
Dieser Artikel beantwortet folgende Fragen:
- Wie kann ich einen Test auf Normalverteilung einfach mit einem Shiny Dashboard durchführen?
- Was versteht man unter Normalverteilung?
- Wie kann man überprüfen, ob Daten normalverteilt sind?
- Gibt es einen Test auf Normalverteilung?
- Was ist der Unterschied zwischen Kolmogorow-Smirnow-Test und Shapiro-Wilk-Test?
Das R Shiny Dashboard
Zunächst stellen wir unser Shiny Dashboard für den Test zur Normalverteilung vor. Danach besprechen wir verschiedene wichtige Aspekte der Normalverteilung und des Testens auf Normalverteilung. Mit dem R package shiny ist es möglich, interaktive, nutzerfreundliche Web-Apps zu erstellen. Für die Analyse von Überlebenszeitdaten hat Novustat eine Shiny Dashboard erstellt.
Benötigen Sie individuell erstelltes Shiny Dashboard? Oder benötigen Sie weitere Beratung zur Auswertung ihrer Daten (z.B. zum Umgang mit nicht normalen Daten)? Wir beraten Sie gerne zu den Themen statistische Programmierung und Datenauswertung.
Umfang des R Shiny Dashboards
Mit Hilfe des Shiny Anwendung kann ein CSV Datensatz eingelesen werden. Jeweils eine Spalte kann auf das Vorliegen einer Normalverteilung überprüft werden. Die Auswahl der Variablenspalte erfolgt im linken Feld. Anschliessend wird in den Reitern das Histogramm mit Normalverteilungskurve ausgegeben. Im nächsten Reiter sind der Boxplot sowie der QQ-Plot zu finden. Im vierten Tab sind die p-Werte der Tests auf Normalverteilung zu finden und die Kenngrössen Schiefe und Kurtosis.
Was heisst hier Normal?
Die Normalverteilung wurde von Carl Friedrich Gauss eingehend beschrieben und wird deshalb auch Gauss-Verteilung genannt. Zeichnet man die Dichtefunktion der Normalverteilung, so ergibt sich eine charakteristische Glockenkurve mit folgenden Eigenschaften:
- Stetige Verteilung mit einem Wertebereich von – ∞ bis + ∞
- Symmetrische Verteilung um den Mittelwert m
- Median, Modus und Mittelwert sind identisch
- Ein Gipfel (unimodal)
- Maximale Dichte im Mittelwert m
- Nahezu alle Werte (99,7%) liegen im Bereich m +/- 3 Standardabweichungen, 2/3 der Werte im Bereich m +/- 1 Standardabweichungen
Die Normalverteilung wird durch die beiden Parameter Mittelwert m und Standardabweichung s eindeutig festgelegt. Als Standardnormalverteilung wird die Normalverteilung mit m = 1 und s = 1 bezeichnet.
Warum ist der Test auf Normalverteilung so wichtig?
Die Normalverteilung nimmt eine zentrale Rolle in der Statistik ein. Viele Verfahren wie parametrische Tests (t-Test, ANOVA), aber auch statistische Modelle wie lineares Regressionsmodell, die Korrelationsanalyse, ja sogar die Clusteranalyse werden für die Berechnung Eigenschaften der Normalverteilung verwendet. Einige Verfahren sind diesbezüglich sehr sensibel, d. h. die Ergebnisse reagieren sehr stark auf eine Abweichung von der Normalverteilung. Andere Verfahren wie beispielsweise die Clusteranalyse benötigen die Eigenschaften der Normalverteilung in der Herleitung der Methodik, funktionieren in der Praxis hinreichend gut bei Abweichungen der Daten von dieser Annahme.
Für die Normalverteilung spielt der zentrale Grenzwertsatz eine wichtige Rolle. Dieser besagt, dass sich die Verteilung der Mittelwerte in der Stichprobe einer Normalverteilung annähert, wenn der Stichprobenumfang gross genug ist. Diese Annäherung ist unabhängig von der Form der zugrunde liegenden Verteilung der Daten. Dabei werden oftmals als Faustregel Stichprobenumfänge ab n = 30 als hinreichend gross beschrieben, ab denen man von normalverteilten Stichprobenverteilungen ausgehen kann.
Welche Arten von Überprüfung auf Normalverteilung gibt es?
Stetige Variablen werden im Vorfeld der Datenanalyse einer Überprüfung unterzogen, ob von einer Normalverteilung ausgegangen werden kann. Diese Überprüfung legt fest, welche Testverfahren verwendet werden können. Bei einer Verletzung der Normalverteilung werden meist nicht-parametrische Verfahren angewendet, die lediglich mindestens ordinal skalierte Variablen voraussetzen, ohne irgendwelche Verteilungsannahmen. Die Überprüfung der Normalverteilung kann entweder explorativ erfolgen oder mit Hilfe eines statistischen Test auf Normalverteilung.
Explorative Überprüfung auf Normalverteilung
Mit Hilfe der explorativen Überprüfung kann man die Variablen per Augenschein mit einer „idealen“ Normalverteilung vergleichen. Wichtige Kriterien sind dabei die Schiefe und Kurtosis der Verteilung. Falls die absoluten Werte von Schiefe und Krümmung (Kurtosis) unter 1 liegen, wird die Abweichung zur Normalverteilung als unbedenklich eingestuft.
Ein Histogramm der Daten mit überlagerter Normalverteilungskurve bietet einen guten Anhaltspunkt für die Beurteilung von Symmetrie, Krümmung und Dichte an den Enden.
Eine spezielle grafische Darstellung ist der QQ-Plot.
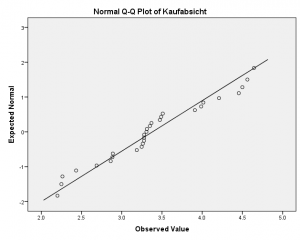
Hier werden die jeweiligen Werte gegen die entsprechenden Quartile der Normalverteilung dargestellt. Bei Vorliegen einer Normalverteilung liegen alle Punkte auf der Winkelhalbierenden des 1. Quadranten des Koordinatensystems. Mit Hilfe dieser grafischen Darstellung lassen sich insbesondere „schwere“ Enden, also zu hohe Wahrscheinlichkeiten extremer Werte, sehr gut diagnostizieren.
Die Schwierigkeit all dieser explorativen Verfahren liegt darin, dass sich in der Praxis immer leichte Abweichungen von einer idealen Normalverteilung zeigen. Die Entscheidung, ob diese Abweichungen schon massgeblich dafür sind, von einer Verletzung, der Normalverteilung zu sprechen, ist selbst für Experten oftmals schwer zu treffen. Aus diesem Grund wird vielfach ein statistischer Test auf Normalverteilung durchgeführt.
Statistischer Test auf Normalverteilung
Ein statistischer Test auf Normalverteilung liefert eine reproduzierbare Entscheidung für das Abweichen einer Variable von einer Normalverteilung. Dabei wird im Test auf Normalverteilung die Alternativhypothese „Die Daten weichen von einer Normalverteilung ab“ überprüft. Das Vorliegen einer Normalverteilung kann dahingegen niemals direkt nachgewiesen werden. Zwei Testverfahren sind für die Überprüfung auf Normalverteilung gebräuchlich:
Kolmororow-Smirnov Test
Beim Kolmogorow-Smirnow Test werden die beobachteten Häufigkeiten der Stichprobe mit den unter Normalverteilung erwarteten Werten verglichen. Dabei geht jeweils die im Intervall höchste betragsmässige Abweichung in die Teststatistik ein. Wird dabei ein Grenzwert überschritten, geht man davon aus, dass die Abweichungen zu hoch sind, und die Alternative – also Verletzung der Normalverteilung als nachgewiesen gilt. Das Testergebnis wird als p-Wert ausgegeben. Liegt der p-Wert unter dem Signifikanzniveau (i. d. R. 5 %), so gilt eine Abweichung der Normalverteilung als nachgewiesen.
Der Kolmogorow-Smirnow Test wird v. a. bei mittleren bis grossen Stichprobenumfang angewendet und kann auf alle Skalenniveaus angewendet werden. Bei kategorialen Merkmalen sorgt die Lilleforce Korrektur für eine bessere Testgüte.
Shapiro-Wilk-Test
Der Shapiro-Wilk-Test ist rechenintensiv und kann gut bei sehr kleinem Stichprobenumfang eingesetzt werden. Die Testentscheidung wird aufgrund des Varianzverhältnisses von unter Normalverteilung erwarteter Varianz und Stichprobenvarianz gebildet. Die Teststatistik ist somit die Korrelation zwischen erwarteten und beobachteten Werten. Das Testergebnis wird als p-Wert angegeben. Liegt der p-Wert unter dem Signifikanzniveau, so gilt eine Abweichung von der Normalverteilung als nachgewiesen.
Statistischer Test auf Normalverteilung: Pro und Kontra
So angenehm eine eindeutige, nachvollziehbare Entscheidung mit einem Test auf Normalverteilung erscheinen mag – Kolmogorow-Smirnow Test und Shapiro-Wilk-Test haben einen eindeutigen Nachteil: Sie reagieren sehr sensibel auf den Stichprobenumfang. Bei grossen Stichproben reichen oft minimale Abweichungen von der idealen Verteilung aus, um p-Werte unterhalb des Signifikanzniveaus zu erhalten und damit einen Nachweis, dass keine Normalverteilung vorliegt. Diese Abweichung muss in der explorativen Analyse kaum in Erscheinung treten, geschweige denn praktische Relevanz haben.
Dieses Hintergrunds sollte man sich als Anwender bewusst sein. Der Test auf Normalverteilung kann nur ein Abweichen von der Normalverteilung nachweisen. Für diesen Nachweis genügen bei hohem Stichprobenumfang bereits minimale, praktisch nicht relevante Unterschiede aus. Eine Überprüfung sollte deshalb nie ausschliesslich aufgrund eines Tests wie dem Kolmogorow-Smirnow Test oder Shapiro-Wilk-Test erfolgen, sondern immer die explorative Überprüfung mit einschiessen.
Schlimmstenfalls werden Tests für die Überprüfung der Hypothesen eingesetzt, die eine geringere Teststärke haben und vorhandene Effekte können nicht nachgewiesen werden.
Zusammenfassung
Die Überprüfung der Normalverteilungsannahme von Variablen wird standardmässig vor der Datenanalyse durchgeführt, da hierbei die Testverfahren festgelegt werden. Trennscharfe parametrische Testverfahren, beruhen wesentlich auf einer Normalverteilung. Es existieren häufig auch allgemeingültige Verfahren, die jedoch weniger trennscharfe sind (nicht-parametrische Verfahren). Die Überprüfung der Normalverteilung erfolgt einerseits explorativ, andererseits können statistische Tests wie der Kolmogorow-Smirnow Test oder der Shapiro-Wilk-Test angewendet werden, um eine Entscheidung zu erhalten. Explorative Verfahren erfordern ein argumentatives Vorgehen in der Rechtfertigung für eine Normalverteilung und sind stark Anwender abhängig. Ein statistischer Test auf Normalverteilung kann eine Abweichung von der Normalverteilung nachweisen. Allerdings reagieren bei grossen Stichprobenumfang sowohl der Kolmogorow-Smirnow Test als auch der Shapiro-Wilk-Test sehr stark auf minimale Abweichungen und führen so letztendlich zu einer Ablehnung der Normalverteilungsannahme, auch wenn diese Abweichungen praktisch nicht relevant sind.
Mit Hilfe des R Shiny Dashboards haben wir die gebräuchlichsten Methoden zur Überprüfung der Normalverteilung eines Merkmals übersichtlich zusammengestellt. Die Entscheidung hinsichtlich der Verteilung muss letztendlich der Anwender treffen, auch unter Berücksichtigung des Anwendungsbezugs.